integrals (area and volumes) (things to remember)

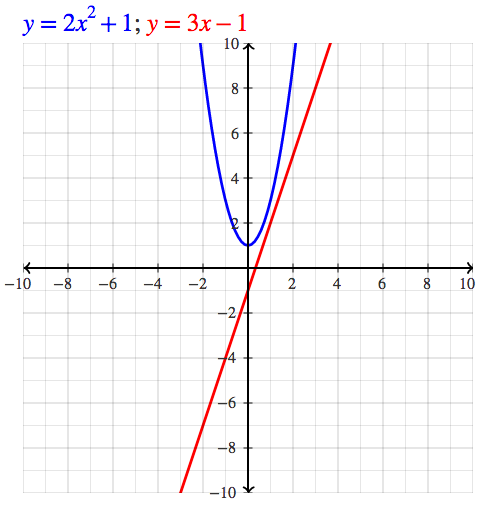
Basic Parabolas (x² + #) and lines

1 1

2 4

Complex parabolas

1 1

2 4

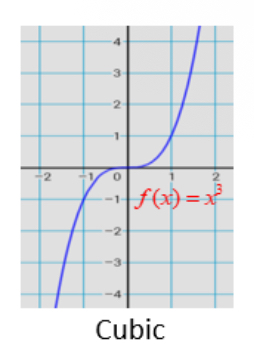
cubic x³

sideways backwards s (starts bottom left to top right)

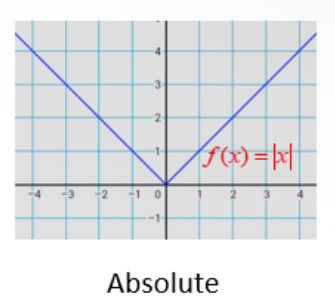
Absolute value |x|

V

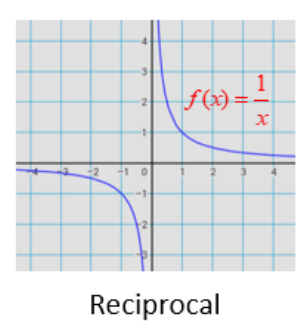
reciprocal 1/x

Top right and bottom left

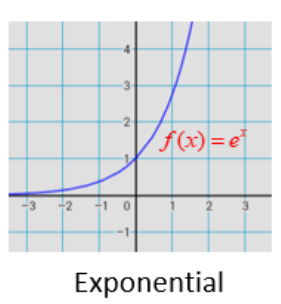
Exponential e^x

tip to memorize: exponent means up (goes up and starts left of x axis) (not below x axis) (goes more up than right) (u shape)

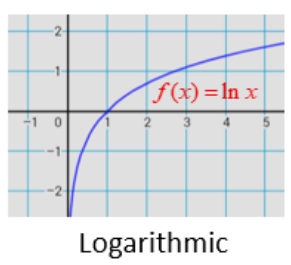
ln x

Starts from bottom right (below x axis) to top right (above axis) (goes more right than up) (c shape)

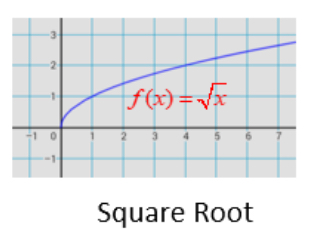
\sqrt{x}

Like ln x but starts from (0,0) (c shape) (goes more right than up)

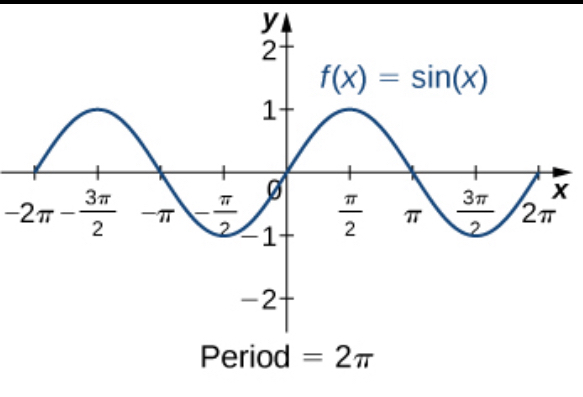
sin x

hill / hump / upside down u starts from zero to pi

parabola/ u shape from zero to pi (continue to the right) (connected like a squiggle)

(period: 2pi)

(X axis is in the middle of all humps)

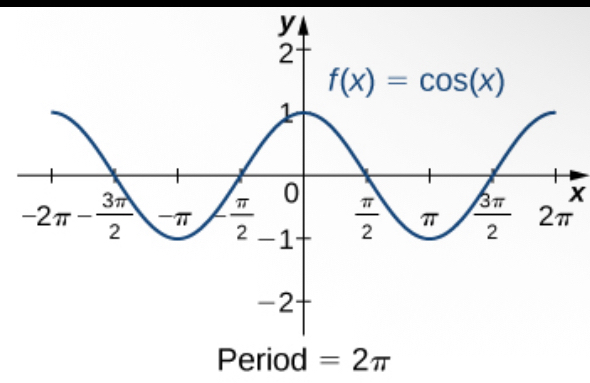
cos x

Y axis in the middle of hump

hill / hump / upside down u starts from negative pi/2 to pi/2

parabola/ u shape from pi/2 to 3pi/2

(continue to the right) (connected like a squiggle)

(period: 2pi)

(X axis is in the middle of all humps)

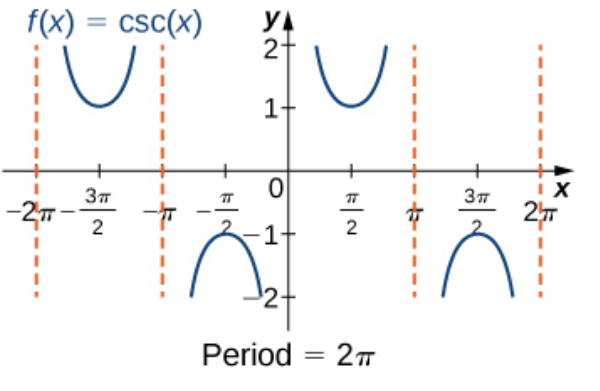
csc x

Parabola u shape from zero to pi

Upsidedown parabola from pi to 2pi

parabolas and upside down parabolas separated by vertical asymptotes (dashed lines)

period: 2pi

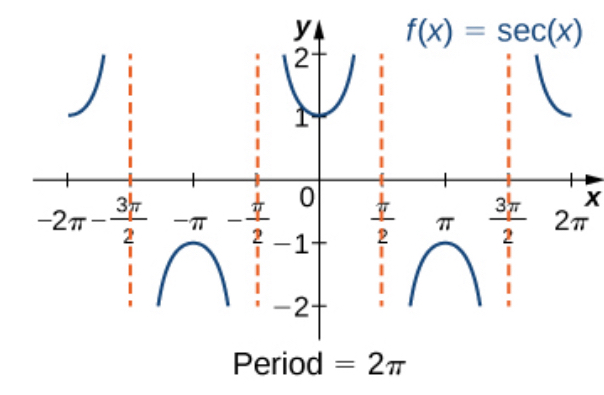
sec x

Y axis in the middle of Parabola u shape

Upsidedown parabola from pi/2 to 3pi/2

parabolas and upside down parabolas separated by vertical asymptotes (dashed lines)

period: 2pi

tan x

y axis in middle

sideways backwards s (going from bottom left to the top right) (goes up)

starts from negative pi/2 to pi/2 and repeats from pi/2 to 3pi/2 (separated with dashed lines (vertical asymptotes))

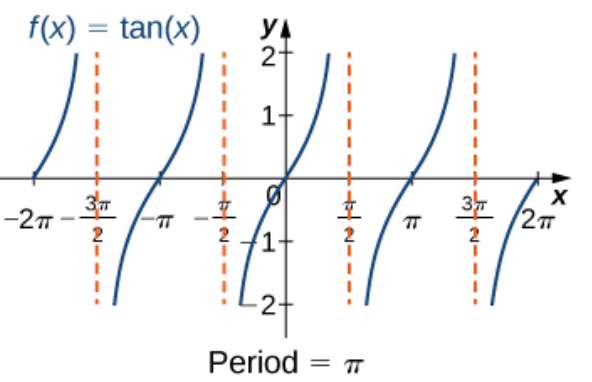
cot x

sideways normal s

Starts from top left to bottom right (goes down)

From zero to pi and pi to 2pi (separated by dashed lines (vertical asymptotes))

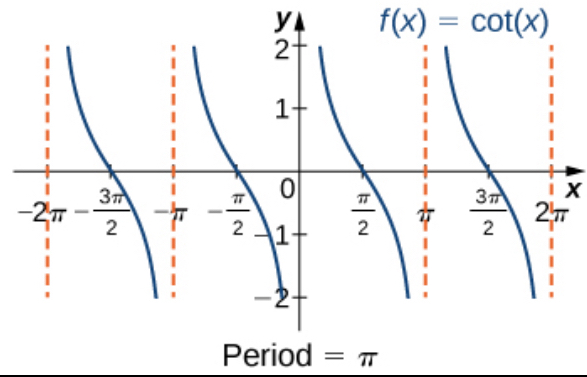
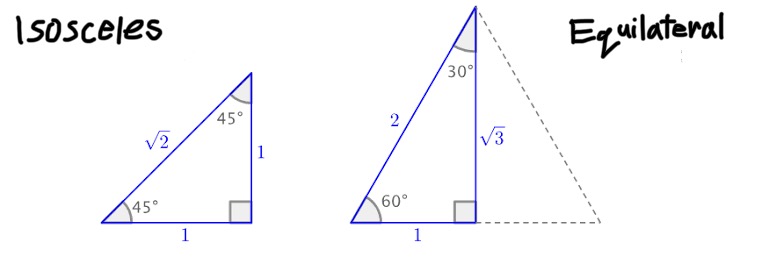
Isosceles and Equilateral Triangles

Pythagorean identities

sin²x + cos²x =1

(Can find the rest of them by either dividing everything by cos²x or sin²x)

use if exponent is odd

Double Angle Formulas (+half angle)

Use if exponent is even

Addition and Subtraction Trig Identities

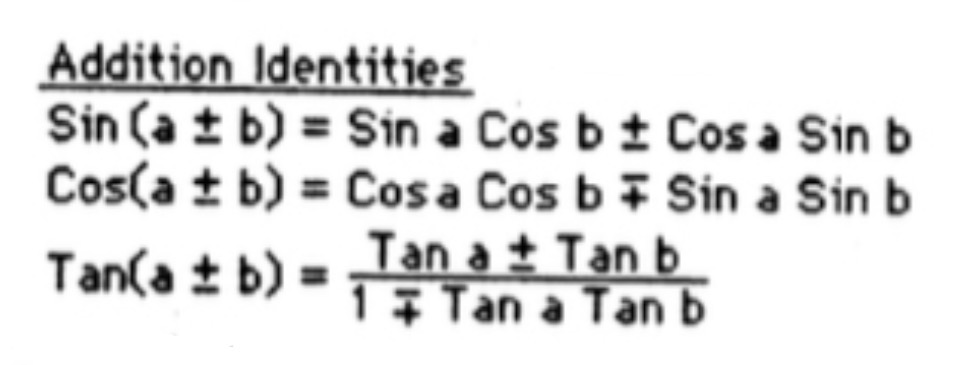
Anti derivative of sec x

ln|tanx + secx|

e^x and In(x) rules

In(e^x) = x

e^(Inx) = x

e^a + e^a = 2e^a (treat like a

variable if power is the same)

e^0=1

In 1 =0

In e=1

e^x cannot equal a negative number

Always e^x= positive number

log_a (b) = In (b) /In(a)

If it looks the same and it is addition or subtraction then add or subtract like you would a variable

derivative of inverse sin and cos

inverse sin = 1/sqrt (1-x^2)

(one over square root one minus x squared)

inverse cos = - 1/sqrt (1-x^2)

(the derivatives of co- trig functions are negative)

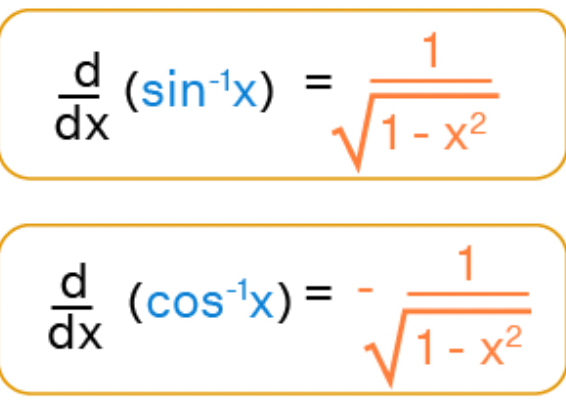
derivative of inverse tan(arctan) and cot

inverse tan = 1/(1+x^2)

(one over one plus x squared) (No square root)

inverse cot = - 1/(1+x^2)

(the derivatives of co- trig functions are negative)

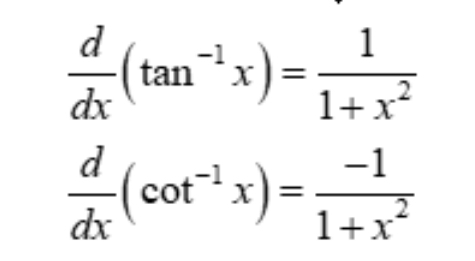
derivative of inverse sec and csc

inverse sec = 1/Ixlsqrt(x^2-1)

(one over absolute value x times square root x squared minus one)

inverse csc = - 1/Ixlsqrt(x^2-1)

(the derivatives of co- trig functions are negative)

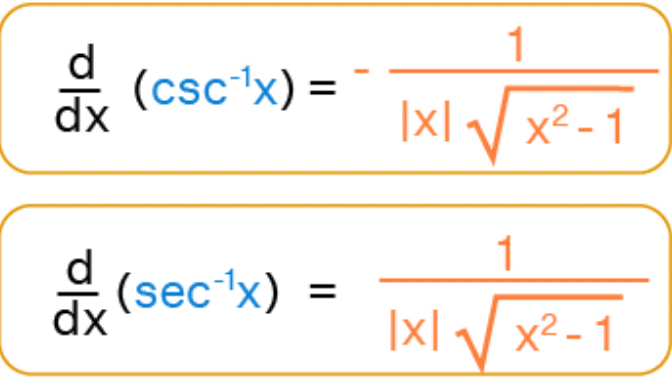
derivative e^x

e^x = e^x

derivative In(x)

1/x

derivative b^x

(b^x) (In(b))

derivative of log_b (x)

1/ (x)(In b)

Discriminant