Gravitation and Circular Motion

Johannes Kepler

________ developed three laws of planetary motion based on the detailed observations of Tycho Brahe.

Keplers laws

________ apply to the orbits of planets.

total mechanical energy

The ________ of the mass in orbit is defined as U + K.

V

________ is the objects velocity.

acceleration vector

The ________ is always directed toward the center of the circle.

positive total mechanical energy

A mass with ________ can escape the gravitational well of the sun; a mass with negative total mechanical energy is bound to orbit the sun.

A Space Shuttle orbits Earth 300 km above the surface. Why can’t the Shuttle orbit 10 km above Earth?

(A) The Space Shuttle cannot go fast enough to maintain such an orbit.

(B) Kepler’s laws forbid an orbit so close to the surface of the Earth. (C) Because r appears in the denominator of Newton’s law of gravitation, the force of gravity is much larger closer to the Earth; this force is too strong to allow such an orbit.

(D) The closer orbit would likely crash into a large mountain such as Everest because of its elliptical nature.

(E) Much of the Shuttle’s kinetic energy would be dissipated as heat in the atmosphere, degrading the orbit.

E—A circular orbit is allowed at any distance from a planet, as long as the satellite moves fast enough. At 300 km above the surface Earth’s atmosphere is practically nonexistent. At 10 km, though, the atmospheric friction would quickly cause the Shuttle to slow down.

Consider two points on a rotating turntable: Point A is very close to the center of rotation, while point B is on the outer rim of the turntable. A penny could be placed on the turntable at either point A or point B.

In which case would the speed of the penny be greater, if it were placed at point A, or if it were placed at point B? Explain.

Both positions take the same time to make a full revolution. But point B must go farther in that same time, so the penny must have bigger speed at point B

Two stars, each of mass M, form a binary system. The stars orbit about a point a distance R from the center of each star, as shown in the diagram above. The stars themselves each have radius r.

In terms of each star’s tangential speed v, what is the centripetal acceleration of each star?

E

the distance used is the radius of the circular motion. Here, because the planets orbit around a point right in between them, this distance is simply R.

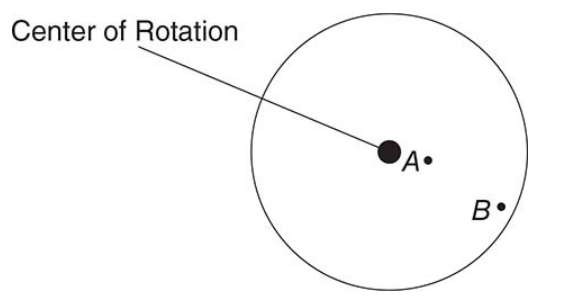
Consider two points on a rotating turntable: Point A is very close to the center of rotation, while point B is on the outer rim of the turntable. A penny could be placed on the turntable at either point A or point B.

At which point would the penny require the larger centripetal force to remain in place? Justify your answer.

The coin needs more centripetal force at point B. The centripetal force is equal to mv2 /r. The speed of a point at radius r is the circumference divided by the time for one rotation T, v = 2πr/T. So the net force equation becomes, after algebraic simplification, Fnet = 4mπ 2r/T 2 . Because both positions take equal times to make a rotation, the coin with the larger distance from the center needs more centripetal force.