Gravitation and Circular Motion
Key Ideas
- Circular motion (and gravitation) problems still require a free-body diagram and the four-step problem-solving process.
- The gravitational force between two objects is bigger for bigger masses and smaller for larger separations between the objects.
- Kepler’s laws apply to the orbits of planets.
Velocity and Acceleration in Circular Motion
Velocity is a vector: an object’s velocity can change either in magnitude or in direction.
When an object maintains the same speed but turns in a circle, the magnitude of its acceleration is constant and directed toward the center of the circle.
The acceleration vector is perpendicular to the velocity vector at any given moment.
The velocity vector is always directed tangent to the circle.
The acceleration vector is always directed toward the center of the circle.
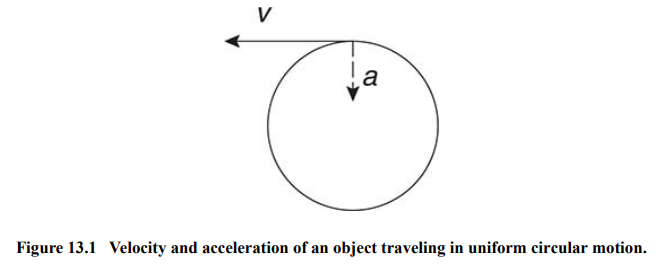
Centripetal Acceleration
The acceleration keeping an object in a uniform circular motion.
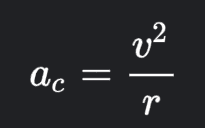
v is the object’s velocity.
r is the radius of the circle in which the object is traveling.
When an object moves in a circle, the acceleration (and also the net force) must point to the center of the circle.
A centripetal force is simply whatever force is directed toward the center of the circle in which the object is traveling.
First, label the forces on your free-body diagram.
Then, find the net force directed toward the center of the circle.
That net force is the centripetal force
Mass on a String
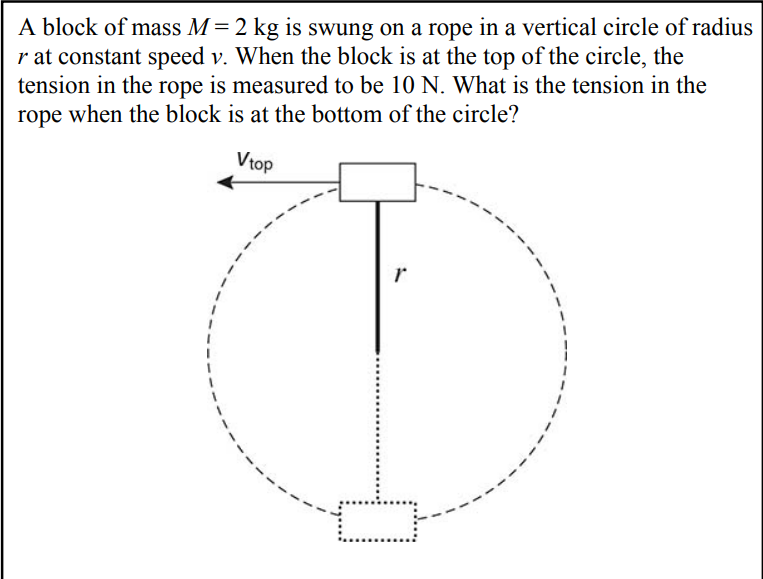
Draw a free-body diagram of the block at the top of the circle and another of the block at the bottom of the circle.

Write Newton’s second law for each diagram.
Acceleration is always toward the center of the circle
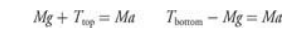
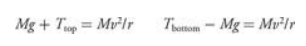
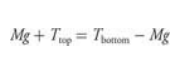
Newton’s Law of Gravitation
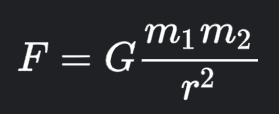
- The gravitational force that one object exerts on another object.
- m1 is the mass of one of the objects
- m2 is the mass of the other object
- r is the distance between the center of mass of each object.
- G is called the “Universal Gravitational Constant”.
Kepler’s Laws
Johannes Kepler developed three laws of planetary motion based on the detailed observations of Tycho Brahe.
Planetary orbits are ellipses, with the sun at one focus.
- Apply this law to a satellite orbiting Earth, in which case the orbit is an ellipse, with Earth at one focus.
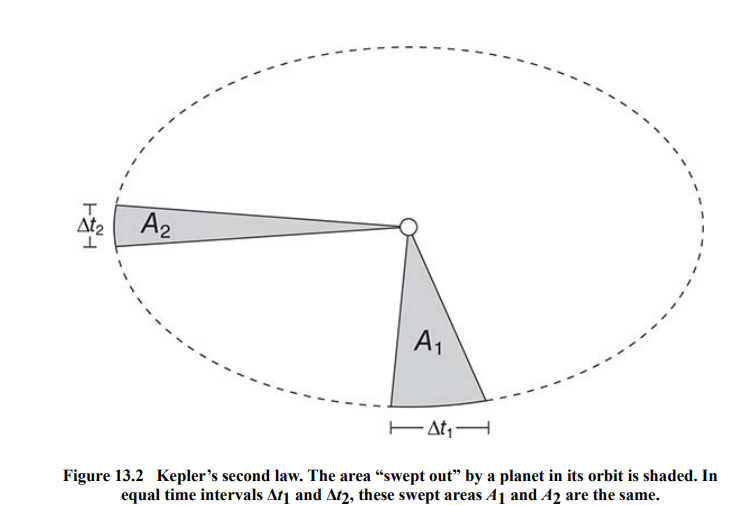
An orbit sweeps out equal areas at equal times.
- If you draw a line from a planet to the sun, this line crosses an equal amount of area for every unit of time.
- When a planet is close to the sun, it must speed up, and when a planet is far from the sun, it must slow down.
A planet’s orbital period squared is proportional to its orbital radius cubed.
- The radius of a non-circular orbit would be the average distance from the sun.
Energy of Closed Orbits
When an object of mass m is in orbit around the sun, its potential energy is ,
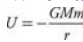
where M is the mass of the sun, and r is the distance between the centers of the two masses
- The total mechanical energy of the mass in orbit is defined as U + K.
- When the mass is in a stable orbit, the total mechanical energy must be less than zero.
- A mass with positive total mechanical energy can escape the gravitational well of the sun; a mass with negative total mechanical energy is bound to orbit the sun.
- All of the above applies to the planets orbiting in the solar system and moons or satellites orbiting planets.
- A useful calculation using the fact that the total mechanical energy of an object in orbit is the potential energy plus the kinetic energy is to find the “escape speed” from the surface of a planet.