Conditional Probability

When one event affect the probability of another event happening and applying those laws

Explain conditional probability

We are shrinking the sample space given the new information because now we know more info about the information we want. Conditioning on an event changes the values we care about.

Conditional Probability Law

For any two events A and B with P(B) > 0 the conditional probabilities of A given B has occurred is defined as

P(A|B) = P(A∩B)/P(B)

Conditional Probability Complement Law

P(A|B) + P(A^c|B) = 1

What should we notice about conditional probabilities?

Notice that P(A|B) ≠ P(B|A) and because we are conditioning on different events we should expect them to be different

Conditional Probability Law (finding unconditional)

P(A∩B) = P(B)P(A|B)

Multiplication Rule for Conditional Probabilities

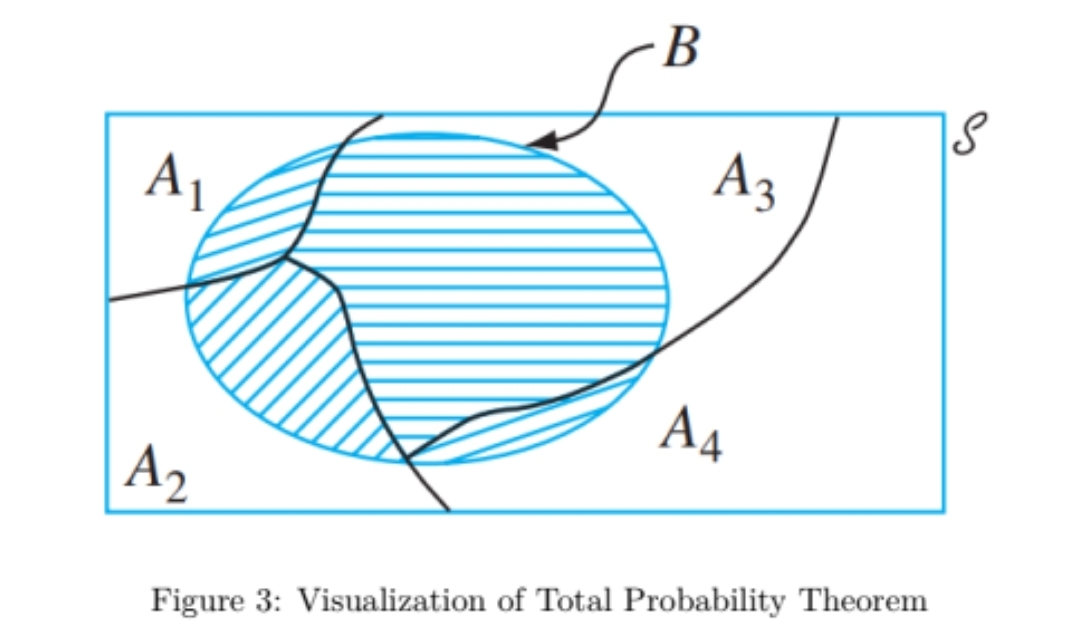
Law of Total Probability

Basically partition are combined to find the probability of one event

P(B) = P(A1∩B)+…..+P(An∩B) is the same as

P(B) = P(A1)P(B|A1)+…..+P(An)P(B|An)

Ex: Let say winning against players but each section of players is different so this is probability based on knowing two things, we divide and conquer.