AP Statistics Unit 1

variable

any characteristic, numbr, or quantity whos values can be changed and measured, counted or observed

Categorical Variable

A variable that can be put into categories but not measured or counted.

Example: Hair color, has a pet, job title

Quantitative Variable

A variable that can be counted or measured

Example: How many pets someone has

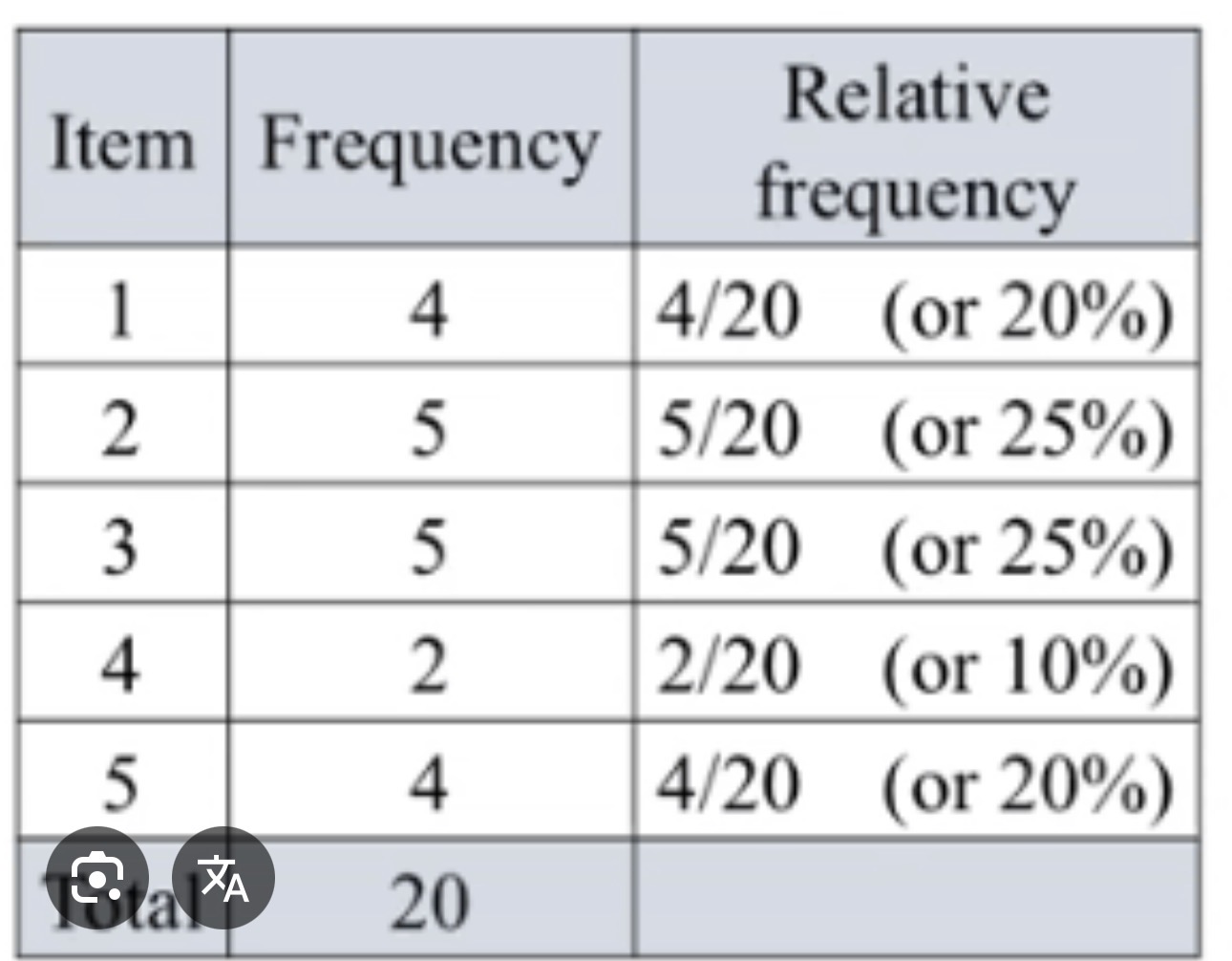
Frequency / Frequency Table

Gives the number of individuals in each category

Relative frequency table

Gives the proportion of individuals in each category

Proportion: frequency/total

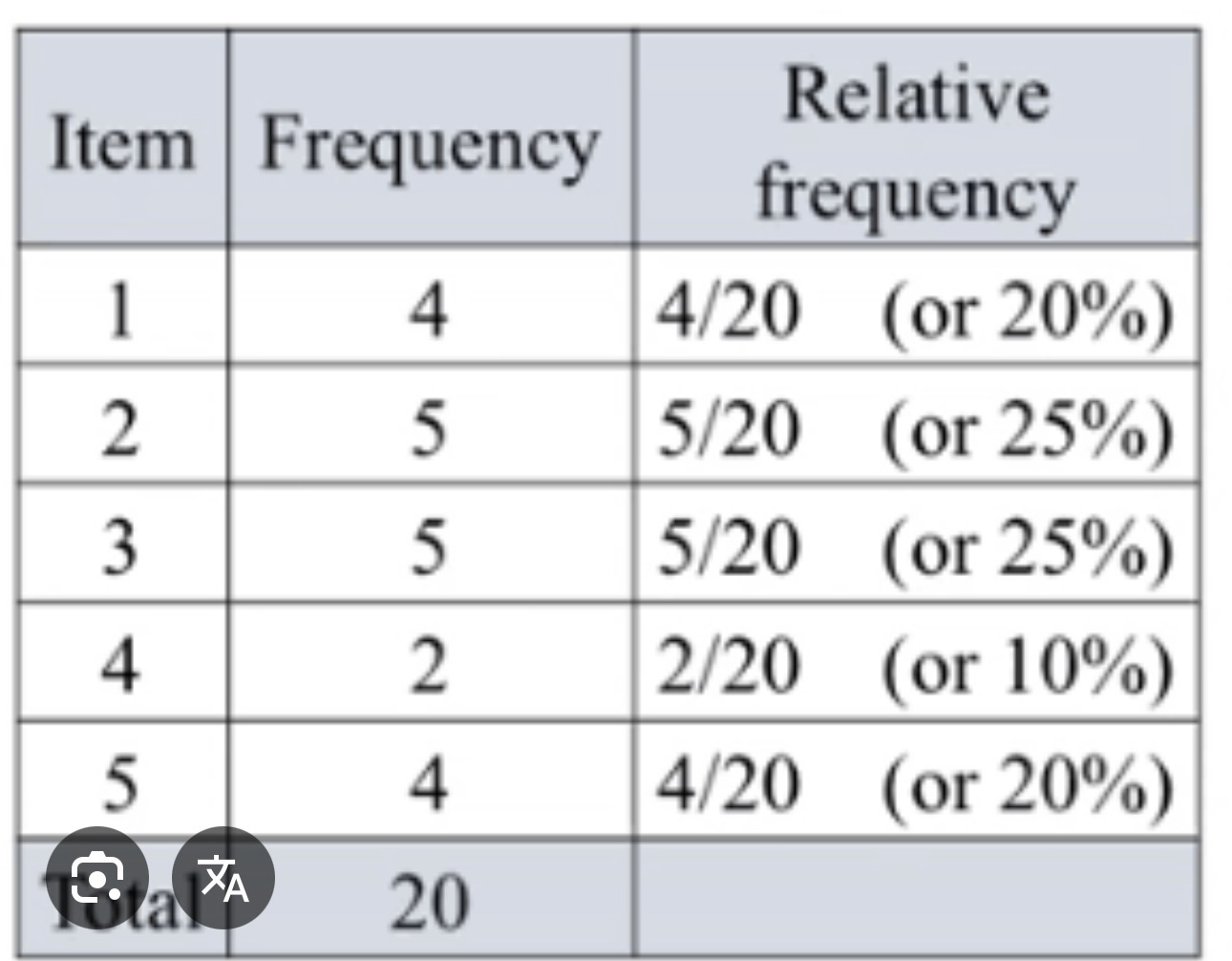
Bar Charts

used to dispay frequencies or relative frequencies for one categorical variable

Discrete Variable

can take on a countable number of values with gaps

Example: number of students in a classroom, website clicks

Continuous Variable

can take on infiinitely many values, but those values cant be counted

Example: height weight, distance

Histogram

Used for quantitative data

Stem and Leaf Plot

used for quantitative data; must have a key

Dotplot

Shape of Distribution

• Skewed right: tail is to the right

• Skewed left: tail is to the left

• Symmetric: no tail

• Unimodal: one peak

• Bimodal: two peaks

• Multimodal: three peaks

• uniform: all bars are the same height

Center of Distribution

• median middle of the data (resistent to outliers)

• mean: sum of all data values divided by the number of values (non-resistent to outliers)

Variability (Spread) of Distribution

• Range: maximum-minimum

• Interquartile Range: difference between q3 and q1

• Standard Deviation: typical distance that each value is away from the meanUn

Unusual Features

• Outliers

• Gaps

• Clusters

Lower Quartile (Q1) and Upper Quartile (Q3)

• Q1 is the median of the first half

• Q3 is the median of the second half

Percentile

the percent of data values (less than or equal to) a given value

• “The value of __ is at the pth percentile. About (p) percent of the values are less than or equal to _”

• Calculate the number of values below it (include that number too) and divide it by the total number of values to find percentile

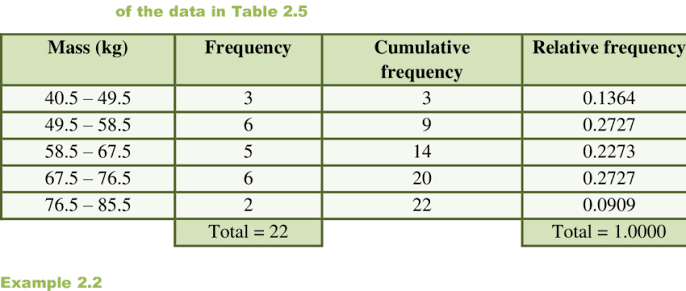
Cumulative Frequency

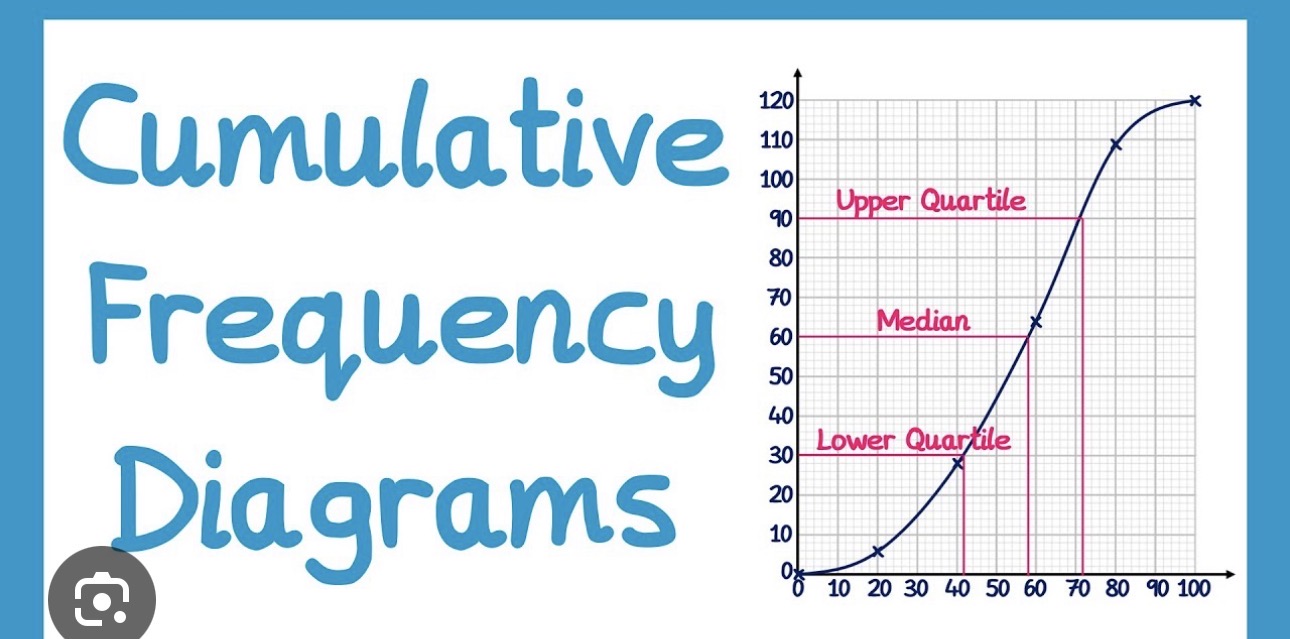
Cumulative Relative Frequency

1.5 IQR Method

• Low outlier is less than Q1 - 1.5 x IQR

• High outliers are greater than Q3 - 1.5 x IQR

Five Number Summary

• miminmum

• Q1

• median

• Q3

• maximum

Box plots

Split data into 4 quartiles

The Normal Distribution

a mound shape and symmetric graph. determined by mean and standard deviation

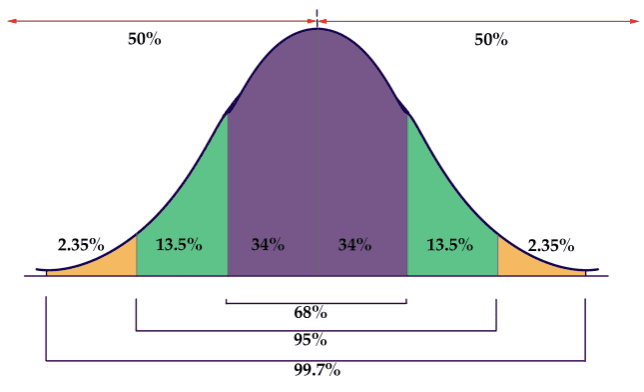
Empirical Rule

• 68-95-99.7

• Within 1 SD of mean = 68% of data

• Within 2 SD of mean = 95% of data

• Within 3 SD of mean = 99.7% of data

Z Score (Standardized Score)

data value-mean/standard deviation

Determining Proportions for Normal Distribution

1. Sketch the normal curve and shade the area in question

2. Calculate a z-score

3. Find the matching Probability using Table A

4. Interpret the probability: “__ percent of (context) is less than (value)”