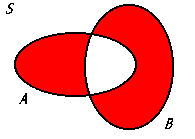
Probability Venn Diagrams
Studied by 0 people
Learn
Practice Test
Spaced Repetition
Match
Flashcards1/15
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
16 Terms
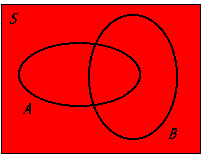
S
A symbol commonly used to represent a sample space in probability, which includes all possible outcomes of a given experiment.
∅
The symbol ∅ represents the empty set, which contains no elements in a probability context.
A
A set representing outcomes in a probability space, often used in conjunction with Venn diagrams to illustrate relationships among different events.
B
A set that can contain elements distinct from those in set A, representing another group in the probability context.
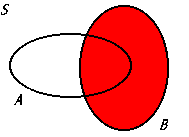
Ac
The complement of set A, representing all elements not in A within a universal set.
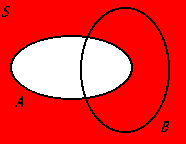
Bc
The complement of event B, representing all outcomes in the sample space that are not included in event B.
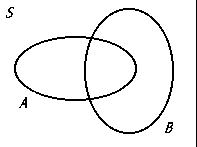
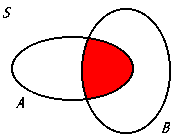
A ∩ B
The intersection of sets A and B, representing all elements that are common to both sets in the probability context.
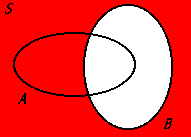
Ac ∩ B
The intersection of the complement of set A and set B, representing all elements that are in set B but not in set A.
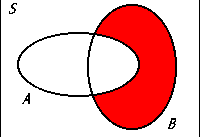
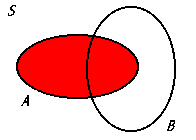
A ∩ Bc
The intersection of set A and the complement of set B, representing all elements that are in set A but not in set B.
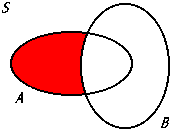
Ac ∩ Bc
The intersection of the complements of sets A and B, representing all elements that are neither in set A nor in set B.
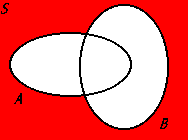
A ∪ B
The union of sets A and B, representing all elements that are in either set A, set B, or both.
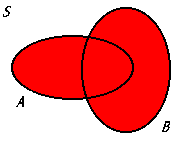
Ac ∪ B
The union of the complement of set A and set B, representing all elements that are either in set B or not in set A.
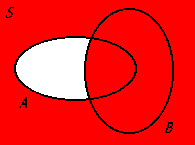
A ∪ Bc
The union of set A and the complement of set B, representing all elements that are either in set A or not in set B.
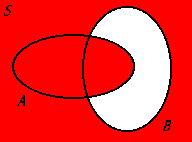
Ac ∪ Bc
The union of the complements of sets A and B, representing all elements that are not in both set A and set B.
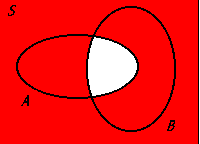
(A ∩ B) ∪ (Ac ∩ Bc)
The union of the intersection of sets A and B with the intersection of their complements, representing all elements that are either in both sets or in neither.
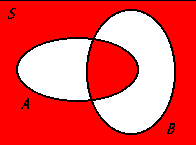
(Ac ∩ B) ∪ (A ∩ Bc)
The union of the intersection of the complement of set A with set B and the intersection of set A with the complement of set B, representing all elements that are in either set A or set B but not in both.
