Chemistry: Measurement, Significant Figures, and Problem Solving

Scientific Notation

A way of writing very large or very small numbers using powers of 10.

Accuracy

How close a measurement is to the true value.

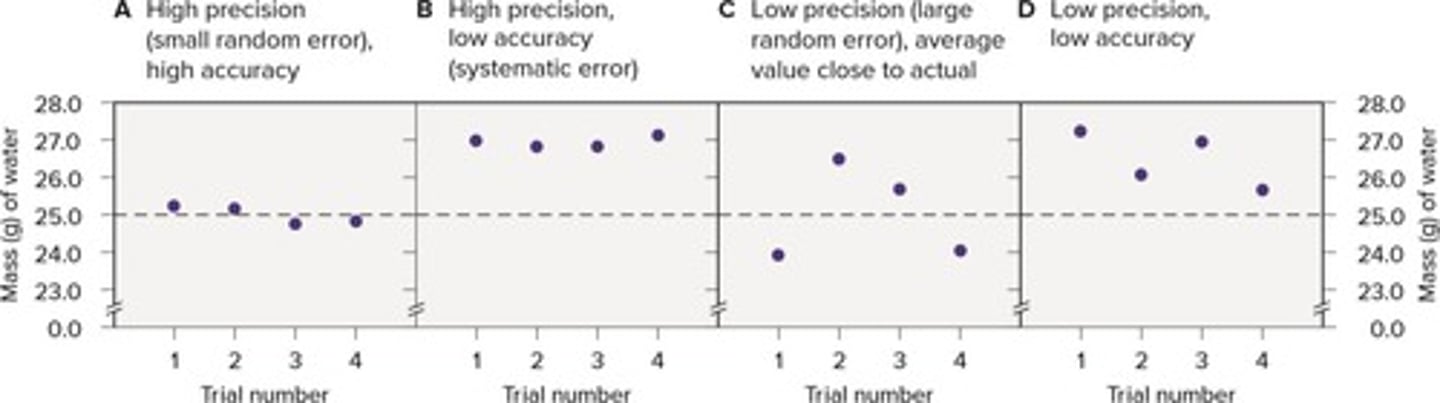
Precision

How close repeated measurements are to each other.

Significant Figures

They reflect how 'certain' (precision) we are in the measurement value and help us know how 'correct' (accuracy) that value is.

Exact Number

A number with no uncertainty in its value; it is known with 100% certainty.

Non-Exact Numbers

Quantities derived from measurements other than counting that have a certain level of uncertainty.

Measurement Uncertainty

The level of uncertainty associated with measurements derived from practical limitations.

Expanded Notation

The form of writing numbers that shows the value of each digit.

Coefficient

The number 'a' in scientific notation, where 1 ≤ a < 10.

Exponent

The number 'n' in scientific notation that indicates the power of 10.

Rounding Rules

The proper methods to adjust numbers to reflect significant figures.

Example of Scientific Notation

4.5×10^4 for large numbers and 0.000000451 for small numbers.

Adjusting the Exponent

To increase the exponent by 1, decrease the coefficient by a factor of 10.

Counting Measurement

An example of an exact number, such as the number of people in a room.

Defined Quantities

Relationships defined by exact quantities, such as 1 ft is exactly 12 in.

Measurement Process Limitations

The practical limitations that lead to uncertainty in non-exact numbers.

Power of 10

The format used in scientific notation to indicate the scale of the number.

Decimal Movement

The process of moving the decimal point to adjust the coefficient in scientific notation.

True Value

The actual value that a measurement aims to reflect.

Finely Measure

The ability to measure with a high degree of precision.

Mass Example

A balance reads a mass of 12.345 g, indicating a specific level of precision.

Estimated Digit

The last digit (rightmost) recorded for a measurement, which is always estimated.

Mass Measurements

All digits displayed are considered significant figures.

Volume Measurements

Use the bottom (or top if inverted) of the meniscus to estimate.

Meniscus

Curved top surface of a liquid.

Non-zeros

These are always counted as significant in reported measurements.

Zeros at the Trailing End

These are significant only if a decimal is explicitly written.

Captive Zeros

Zeros that are 'captive' between non-zeros are significant.

Example of Trailing Zeros

90.0 g is significant, while 90 g is not.

Example of Captive Zeros

105 mL is significant, while 0.015 L is not.

Counting Significant Figures

Use a set of rules to determine how many significant figures are in a number.

Significant Figures in 0.005090 mg

This measurement has four (4) reported significant figures.

Reporting Significant Figures in Calculations

The calculated number cannot contain more certainty than the measurement itself.

Adding Zeros

Must add zeros (and sometimes also use scientific notation) if more digits need to be included.

Multiplication/Division Rule

The calculated value has its sig figs limited by the number from the calculation with the fewest number of sig figs.

Addition/Subtraction Rule

The calculated value has its sig figs limited by the number from the calculation with the least precise place value.

Example of Reporting with Four Sig Figs

Report 85,327 g with four total sig figs.

Example of Including More Digits

Report 85 mg with four total sig figs.

Non-zero digits

Always significant.

Trailing zeros

Significant if they are at the end of a number and a decimal is explicitly written.

Leading zeros

Not significant as they are not at the trailing end nor captive between non-zeros.

Reported significant figures

The number of significant figures in a measurement, e.g., 0.005090 mg has four significant figures.

Calculations with significant figures

The calculated number cannot contain more certainty than the measurement itself.

Example of truncation

Report 85,327 g with four total significant figures.

Example of multiplication/division

For 15.227 nm × 1.054 nm, the result is limited by the number with the fewest significant figures.

Example of addition/subtraction

For 3.45 g + 1.1 g, the result is limited by the least precise place value.

Next lecture preparation

Read Sections 1.6 in the text covering mathematical treatment of units, unit conversions, and using scientific formulas.

Dimensional analysis

The general process of treating units as mathematical quantities in a calculation.

Factor-Label Method

A method that utilizes ratios of equivalent units called conversion factors for unit conversions.

Conversion factor

A ratio between equivalent measurements each expressed in different units.

Scientific formula

A mathematical equation that expresses a relationship between different properties.

Density formula

The formula for density, 𝑑, is a ratio between its mass, 𝑚, and volume, 𝑉: 𝑑=𝑚/𝑉.

Unit conversions

The process of converting a quantity from one unit to another using conversion factors.

Example of unit conversion

1 ft = 12 in (equivalent measurements).

Example of scientific formula

The density of a metal block measuring 2.50 cm x 4.30 cm x 1.90 cm with a density of 7.34 g/cm3.

Combining unit conversions with scientific formulas

Example: What is the density (in g/cm3) of a metal block that has a mass of 0.255 kg and measures 34 mm x 46 mm x 56 mm?

Mathematical Treatment of Measurement Results

Using mathematical equations to describe the relationships between properties.

Example of dimensional analysis

Acts like an 'insurance policy' - if the final units match the property of the unknown, it's a strong indication it was done correctly.

Blueprint for unit conversions

Given unit × desired unit / given unit = desired unit.

Example of radius conversion

The radius of a single neon atom is 1.60 Å. What is its radius in meters? 1 Å= 10^-10 m.

Chemical problem-solving strategies

Various approaches to tackle chemical problems effectively.

Learning Objectives

Use dimensional analysis, factor label method, and scientific formulas to calculate properties.

Phases and Classification of Matter

Different states in which matter exists, categorized based on physical properties.

Physical and Chemical Properties

Characteristics that define the behavior of substances in physical and chemical processes.

Measurements

Quantitative assessments of physical quantities.