Macroeconomics The Long Run

Growth

Growth is the steady increase in aggregate output over time.

Standart of living

Real GDP per person

Output per person

A country’s GDP divided by its population.

Purchasing power

Income in terms of goods

Purchasing power parity PPP

A method of adjustment used to allow for international comparisons of GDP.

Easterlin paradox

The proposition that higher income in a country is not associated with higher levels of happiness.

Force of compounding

The large effects of sustained growth on the level of variable.

Convergence

The tendency for countries with lower output per capita to grow faster, leading to convergence of output per capita across countries.

Maltusian trap

The case of an economy where increases in productivity lead to a decrease in mortality and an increase in population, leaving income per person unchanged.

State of technology

The degree of technological development in a country or industry.

Constant returns to scale

The proposition that a proportional increase (or decrease) of all inputs leads to the same proportional increase (or decrease) in output.

Technological progress

An improvement in a state of technology

Aggregate production function F

Relation bw aggregate output and the inputs in production.

Y - aggregate output,

K - capital, the sum of all machines, plants and buildings in the economy (aggregate capital stock),

N - labor, the number of workers in the economy (aggregate employment)

The function F depends on the state of technology and shows how much output is produced for given quantities of capital and labor.

Constant returns to scale: xY =F(xK,xN)

Decreasing returns to capital: Increases in capital lead to smaller and smaller increases in output.

Decreasing returns to labor: Increases in labor lead to smaller and smaller increases in output.

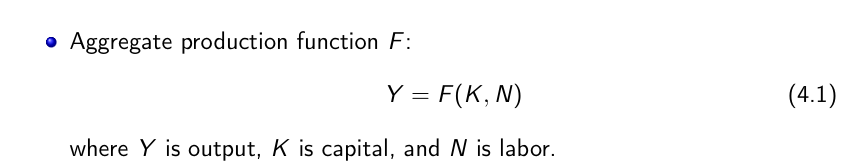
Output and Capital per Worker

Increases in capital per worker: Movements along the production function.

Improvements in the state of technology: Shifts (up) of the production function.

Growth comes from capital accumulation (a higher saving rate) and technological progress (the improvement in the state of technology).

Decreasing returns to capital: Increases in capital per worker lead to smaller and smaller increases in output per worker.

Decreasing returns to labor: Increases in labor, given capital, lead to smaller and smaller increases in output.

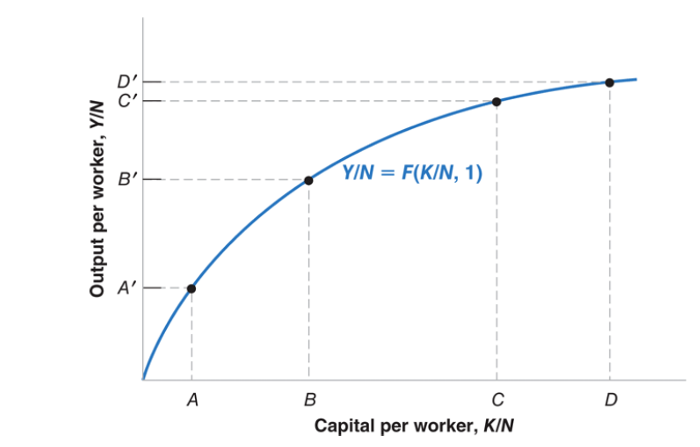
The Effects of an Improvement in the State of Technology

An improvement in technology shifts the production function up, leading to an increase in output per worker for a given level of capital per worker.

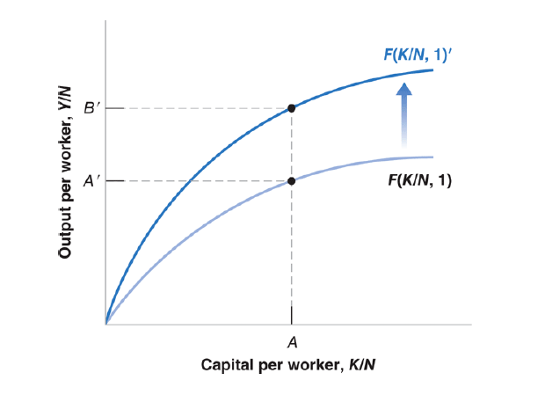
Interactions between Output and Capital

Output in the long run depends on two relations:

▶ The amount of capital determines the amount of output being produced.

▶ The amount of output produced determines the amount of saving, which in turn determines the amount of capital being accumulated over time.

Higher capital per worker leads to higher output per worker.

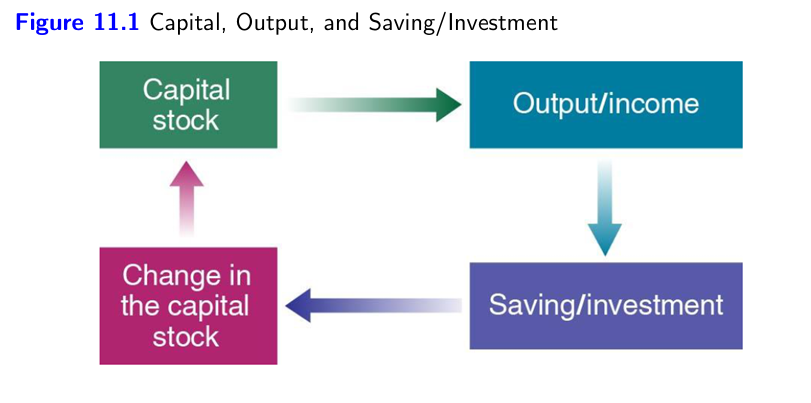
relation between output and investment

Investment is proportional to output.

The higher (lower) output is, the higher (lower) is saving and so the higher (lower) is investment.

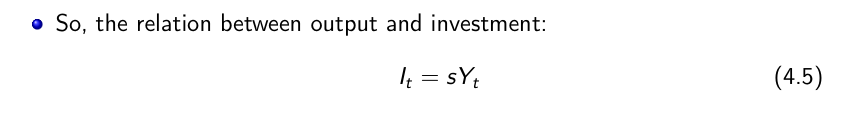
The evolution of the capital stock

If investment per worker exceeds (is less than) depreciation per worker

Capital and Output Dynamics

When capital and output are low, investment exceeds depreciation and capital increases.

When capital and output are high, investment is less than depreciation and capital decreases.

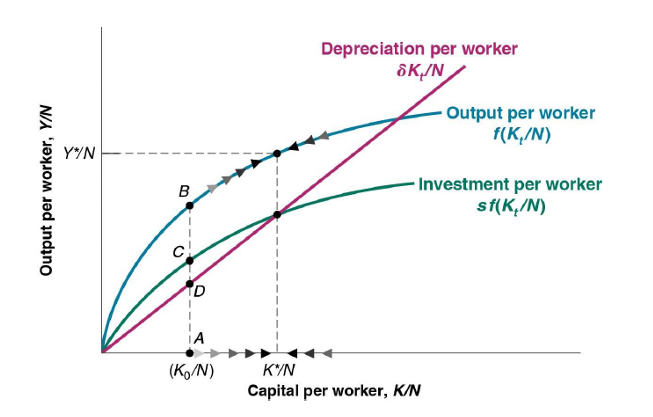
Steady state

The Effects of Different Saving Rates

A country with a higher saving rate achieves a higher steady-state level of output per worker.

The saving rate has no effect on the long-run growth rate of output per worker, which is equal to zero.

The saving rate determines the level of output per worker in the long run.

An increase in the saving rate will lead to higher growth of output per worker for some time, but not forever.

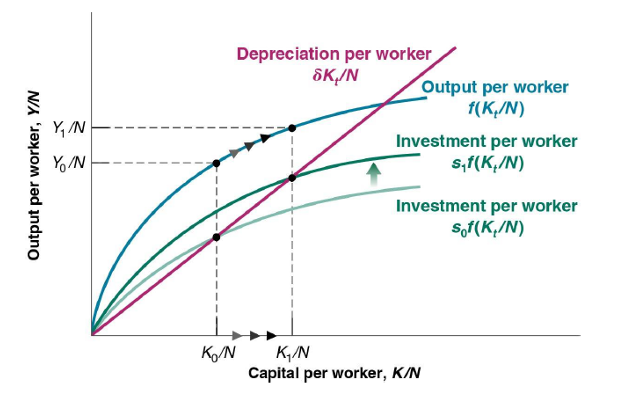
The Effects of an Increase in the Saving Rate on Output per Worker in an Economy Without Technological Progress

An increase in the saving rate leads to a period of higher growth until output reaches its new higher steady-state level.

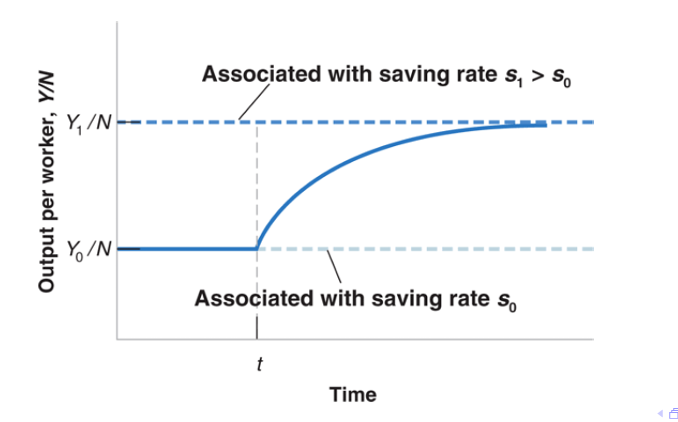
The Effects of an Increase in the Saving Rate on Output per Worker in an Economy with Technological Progress

An increase in the saving rate leads to a period of higher growth until output reaches its new higher steady-state level (balanced growth path).

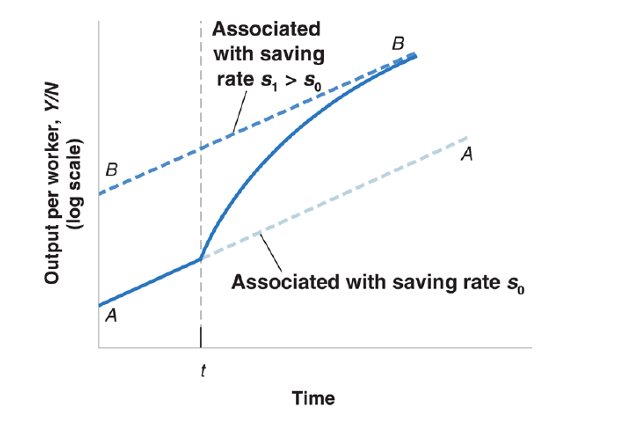
The Implications of Alternative Saving Rates

What matters to people is not how much is produced, but how much they consume.

Governments can affect the saving rate by:

▶ changing public saving (budget surplus)

▶ using taxes to affect private saving

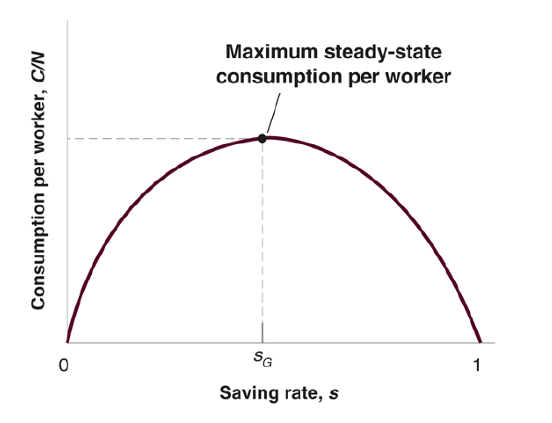
Golden-rule level of capital: The level of capital associated with the saving rate that yields the highest level of consumption in steady state

For a saving rate between zero and the golden-rule level, a higher saving rate leads to higher capital per worker, higher output per worker and higher consumption per worker.

For a saving rate greater than the golden-rule level, a higher saving rate still leads to higher capital per worker and output per worker, but lower consumption per worker.

An increase in the saving rate leads to lower consumption for some time but higher consumption later.

The Effects of the Saving Rate on Steady-State Consumption per Worker

An increase in the saving rate leads to an increase, then to a decrease in steady-state consumption per worker.

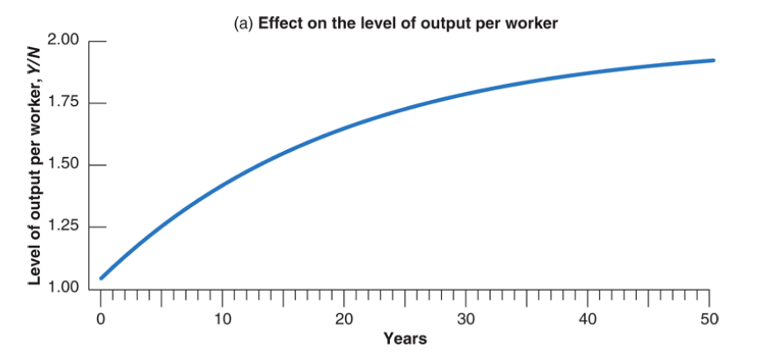
The Dynamic Effects of an Increase in the Saving Rate from 10% to 20% on the Level and the Growth Rate of Output per Worker

It takes a long time for output to adjust to its new higher level after an increase in the saving rate. Put another way, an increase in the saving rate leads to a long period of higher growth.

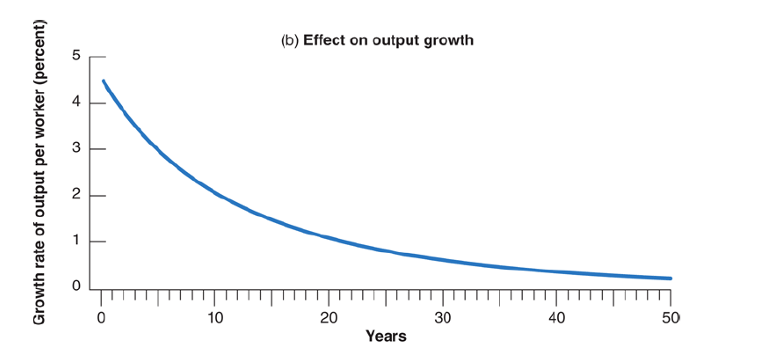
The Dynamic Effects of an Increase in the Saving Rate from 10% to 20% on the Level and the Growth Rate of Output per Worker

It takes a long time for output to adjust to its new higher level after an increase in the saving rate. Put another way, an increase in the saving rate leads to a long period of higher growth.

consumption per worker

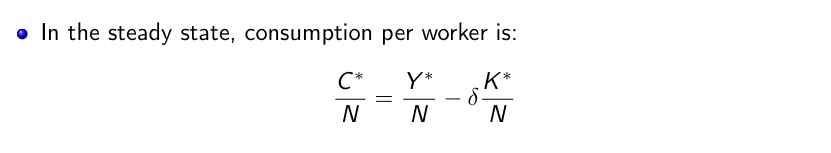
The Saving Rate and the Steady-State Levels of Capital, Output, and Consumption per Worker

Cobb-Douglas production function

Cobb-Douglas Production Function 2

Physical versus Human Capital

Technological progress can lead to

Technological progress can lead to:

▶ larger quantities of output for given quantities of capital and labor

▶ better products

▶ new products

▶ a large variety of products

The state of technology (A) is a variable that tells us how much output can be produced from given amounts of capital and labor at any time:

Y =F(K,AN)

so AN is the amount of effective labor.

With constant returns to scale and a given state of technology (A), if the amounts of capital and labor changes by x times, output changes by x times:

xY =F(xK,xAN)

If x = 1/AN, output per effective worker is a function of capital per effective worker:

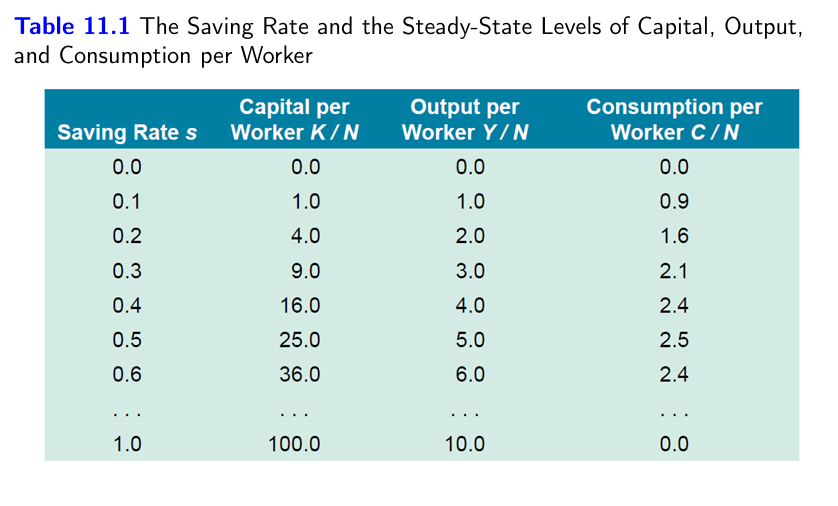
Y/AN =f(K/AN)

Output per Effective Worker versus Capital per Effective Worker

Because of decreasing returns to capital, increases in capital per effective worker lead to smaller and smaller increases in output per effective worker.

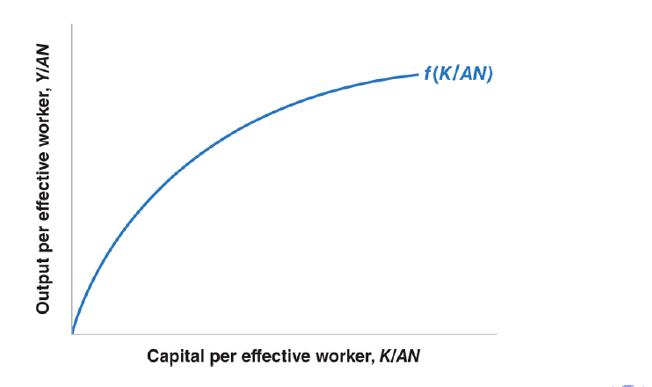
the level of investment per effective worker needed to maintain a given level of capital per effective worker

The Dynamics of Capital per Effective Worker and Output per Effective Worker.

Capital per effective worker and output per effective worker converge to constant values in the long run.

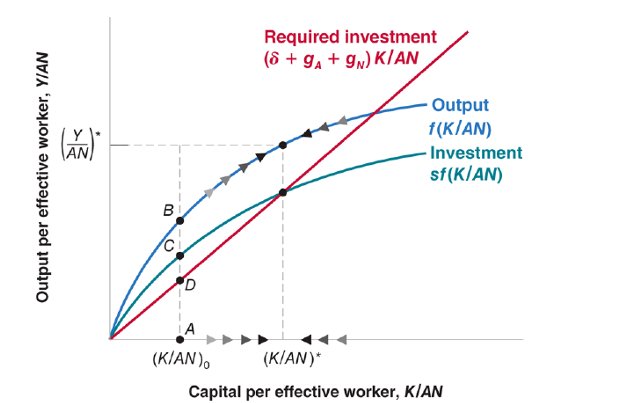
steady state of the economy

The steady state of the economy is such that capital per effective worker and output per worker are constant, and equal to (K/AN)∗ and (Y/AN)∗, respectively.

When the economy is in steady state, output per worker grows at the rate of technological progress (gA).

The Characteristics of Balanced Growth

On the balanced growth path (steady state or long run):

▶ Capital per effective worker and output per effective worker are constant.

▶ Capital per worker and output per worker are growing at the rate of technological progress.

▶ Capital and output are growing at a rate equal to the sum of population growth and the rate of technological progress.

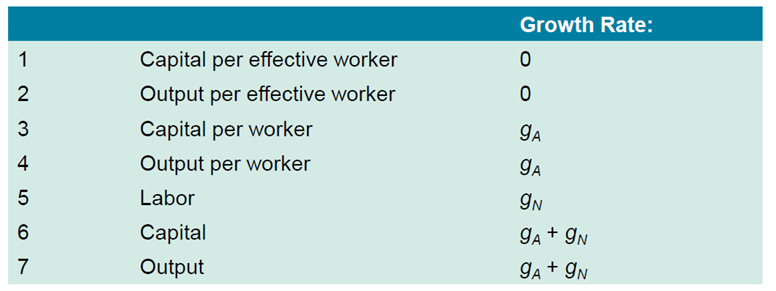
The Effects of an Increase in the Saving Rate: I

An increase in the saving rate leads to an increase in the steady-state levels of output per effective worker and capital per effective worker.

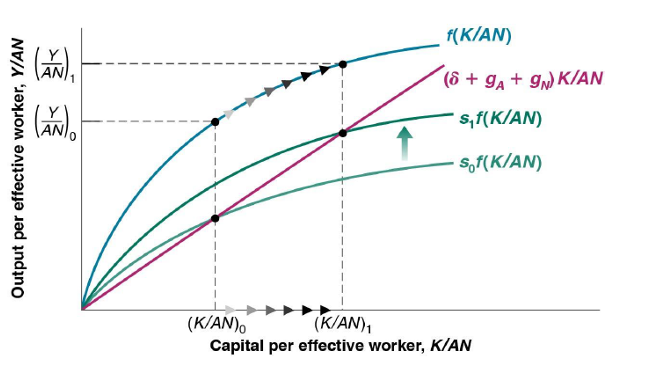
The Effects of an Increase in the Saving Rate: II

The increase in the saving rate leads to higher growth until the economy reaches its new, higher, balance growth path

The Determinants of Technological Progress

To sustain growth, advanced countries that are at the technology frontier must innovate.

Most technological progress is the outcome of firms’ research and development (R&D) activities.

The level of R&D spending depends not only on the fertility of research (how spending on R&D translates into new ideas and new products) but also on the appropriability of research results (the extent to which firms can benefit from the results of their own R&D).

Patents give a firm that has discovered a new product the right to exclude anyone else from the production or use of that new product for some time.

There is a strong positive relation between the degree of protection from expropriation and the level of GDP per person. This highlights the importance of the protection of property rights

Summary

In the steady state (balanced growth path), the growth rate of production and capital stock corresponds to the sum of the population growth rate (g_N) and the rate of technological progress (g_A).

This growth rate of production is independent of the saving rate.

However, the saving rate affects the steady-state level of production per effective labor.

An increase in the saving rate temporarily pushes the growth rate above steady-state growth.