CUESTIONES DE TEORIA PARA EL EXAMEN DE HISTORIA DE LAS MATEMATICAS

La matemática mesopotámica

• Early writings that are considered formal in 3400-3200 BC are generally found on clay tablets. The writing evolved into cuneiform (wedge-shaped characters used in the ancient writing systems of Mesopotamia). Numerical representations were present from the beginning. It includes an immense amount of tablets.

• Numeration system: positional in base 60. Symbols fro 1 to 59 are constructed in base 10, adding: Y-shaped mark=1, triangular wege=10. Using these numbers, any value can be constructed. For example, 1⋅60+22=82 and 20⋅60² + 2⋅60^1+11= 72131 (look back at notes for visual representation)

  Difficulties: There wasn’t a symbol for zero until approximately 300BC where they used a symbol (slanted double wedge). Moreover, numbers were written without spaces between digits making it harder to interpret. There were decimals, but no special symbols for them. So wedgearrowarrow could be interpreted as 1⋅60+20 or 1+20⋅60^-1. So context is necessary fo rinterpreting the numbers.

• Why base 60? Likely due to practical reasons (divisibility, lunar cycles etc.)

• Sources: Many tablets exist but represent a small percentage of total records, though the quantity i still notable. These tablets mainly present practical problems and solutions, with fewer theoretical explanations and proofs. Practical focus but with problems of an exclusively mathematical value. Strong emphasis on arithmetic.

• YBC 7829 is a Babylonian clay tablet notable for containing an accurate approximation to the square root of 2, the length of the diagonal of a unit square, given to the accuracy of 6 decimal places. Believed to be the work of a student from some time between 1800 and 1600 BC. Approximates the diagonal of a square of side length 30.

• Example AO650: Problem: calculate how much time is needed to double a loaned amount of money with an annual compound interest rate of 20%

• Example BM13901 (14 problems o equations or systems of quadratic equations): Problem: Calculate the area of a square, given that its area minus its side is 870. That is to say, they worked with quadratic equations. For cubics, they constructed long tables for n³, n³+n, n³-n, n³+n²,… and approximated solutions

• Mesopotamian geometry was less detailed than Egyptian geometry. The approximation of pi was traditionally 3, but they also sometimes used 3+1/8=3.125

• Tell Harmal clay tablet:The tablets contain a wide range of mathematical problems and solutions, showcasing the advanced level of Mesopotamian mathematics during the period.

  They include: Problems related to geometry (triangles, areas, and volumes). Arithmetic exercises involving fractions, proportions, and multiplication. Algebraic equations, including linear and quadratic equations. Some problems demonstrate the use of the Pythagorean theorem centuries before it was formally recorded in Greek texts.

• Plimpton 322 is a Mesopotamian clay tablet written in cuneiform that dates back to around 1800 BCE. This tablet is particularly significant because it contains a list of Pythagorean triples. It demonstrates an understanding of principles later associated with the Pythagorean theorem, centuries before Pythagoras.

  Plimpton 322 is a table with 15 rows and 4 columns (though one column is broken off). Each row represents a different Pythagorean triple, and the remaining columns include numbers and ratios related to the triples. The tablet might have been used to help them solve practical problems involving right triangles, such as in surveying or construction.

Los tres problemas célebres de la geometría en la Grecía Clásica (siglo V a.C.) y algunos avances

1. Squaring the circle (Quadrature of the circle)

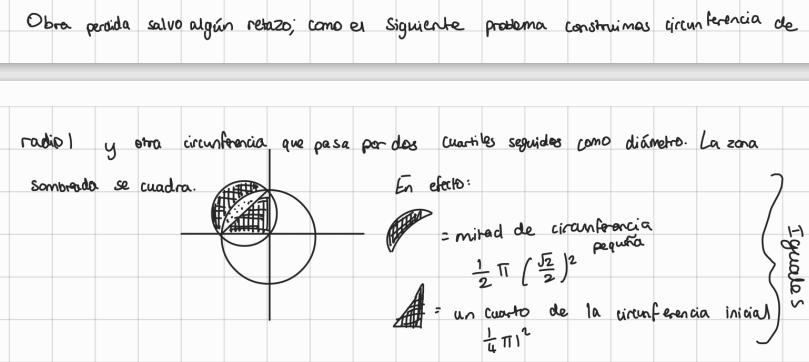
   Problem: Construct a square with the same area as a given circle using only a compass and straightedge. Mathematically: given a circle of radius R, construct a square with area πR². However, it was proven to be impossible with a compass and straightedge by Ferdinand Lindemann in 1882 because the problem requires the exact construction of V which was proven to be transcendental (by him as well). A transcendental number cannot be constructed geometrically with finite steps. Hippocrates of Chios (470-410 BC) partially resolved related problems by squaring lunes (crescent-shaped regions) showing how portions of circular areas could be squared using geometry. His work paved the way for later mathematical exploration, even though the full problem remained unsolvable.

   Here’s the problem: a circle is constructed with radius r, and a second circle is drawn using 2 points on the first circle (a quarter-circle) as the diameter. This creates an overlapping lune (the shaded region). The shaded lune is proven to have the same area as a quarter-circle.

2. Doubling the cube (Delian problem)

   Problem: construct a cube with twice the volume of a given cube using only a compass and a straight edge. Mathematically, given a cube of side L, construct a cube with side length ³(sqrt2(L)). It is not possible because the problem requires constructing ³(sqrt2) or 2_^1/3 which is not a constructible number (proven by the Wantzel theorem in 1837. According to legend, the problem originated when the Oracle of Delphi suggested doubling an altar to appease the gods during a plague. This led to attempts to geometrically solve the problem.

   Archytas of Tarentum (430–360 BCE) made significant contributions using a combination of geometric curves and 3D methods, demonstrating advanced understanding of spatial geometry.

   Menaechmus used conic sections (parabolas and hyperbolas) to solve the problem algebraically, though this method was beyond the compass-and-straightedge restriction.

3. Trisecting an angle

   Problem: divide any given angle into three equal parts using only a compass and straight edge

   For most angles, trisecting involves solving a cubic equation, which cannot be done with compass and straightedge (proven in 1837 by Pierre Wantzel)

   Historical attempts: Hippias of Elis (443-399 BC) introduced the quadratrix, a curve generated by the intersection of two moving lines, which could trisect any angle. However, this method did not work within the compass and straight edge restriction. Trisection spurred the exploration of neusis constructions to solve the problem (which didn’t count for the greeks because it involves the use of a MARKED straight edge with specific marks on.

Euclides de Alejandría

Euclid of Alexandria (323–285 BCE)

• Euclid owes his name to the capital of Egypt, Alexandria, established by Ptolemy (a general of Alexander the Great). Ptolemy also created the Mouseion, a center of study.

• Euclid travelled to Alexandria and became a professor at the Mouseion, which motivated him to write his mathematical manual: Elements.

Structure of Euclid's Elements

• Composed of 13 books:

  • Books I–VI: Plane geometry.

  • Books VII–IX: Number theory and the theory of incommensurability.

  • Books X–XIII: Spatial geometry.

Book I

• Begins with 23 definitions and highlights 5 postulates:

The Five Postulates:

1. Two distinct points determine a line segment.

2. A straight line can extend indefinitely.

3. A circle can be drawn given a center and any radius.

4. All right angles are equal.

5. If a line intersects two others such that the sum of the interior angles on the same side is less than 180∘ , the two lines, when extended, will meet on that side.

   • Equivalent to Postulate 5.1: For a point outside a line, there is only one parallel to the given line.

   • Equivalent to Postulate 5.2: The sum of the angles in a triangle is 180∘.

Controversy Around the Fifth Postulate

• Over time, debates arose about whether the fifth postulate depended on the others.

• hard to be proved

• In the 19th century, alternative geometries emerged by rejecting the fifth postulate, leading to:

  • Hyperbolic geometry.

  • Spherical geometry.

• Questions were also raised about whether Euclid’s axioms were sufficient.

  • Hilbert restructured Euclid’s axiomatic system in 1889, creating a version with 20 postulates.

Later Editions of Elements

• Proclus, in a later edition, argued that Euclid’s work compiled the results of earlier mathematicians, formally proving existing knowledge.

• Major influences:

  • Pythagoras: Books I and II.

  • Hippocrates of Chios: Books III and IV.

  • Eudoxus: Book V.

  • Theaetetus: Books XI, XII, and XIII.

Copies of the Elements

• The first fragment of the Elements was found in Oxyrhynchus in 100 CE.

• The first complete copy was discovered in the 6th century CE (currently housed in the Vatican Library).

• The work did not arrive in Spain until 1576 CE, through Arabic translations.

Arquímedes de Siracusa

Archimedes of Syracuse (282–212 BCE)

• Archimedes is considered the first known mathematical investigator/researcher. A brilliant mathematician and physicist (known for his law of the lever), he wrote books with original contributions. However, we don’t know of all his work as much of his work was not widely distributed.

• His lost work "The Method" was rediscovered in 1909 in a palimpsest (a text written over another erased one). This work includes explanations of his proofs, motivations, and discoveries.

Key Contributions:

1. Equilibrium of Planes:

   • Archimedes formulated the law of the lever. This states that if the distance from the fulcrum to where the input force is applied is greater than the distance to where the ouput force is applied, the lever amplifies the input force

2. Floating Bodies:

   • Established Archimedes' principle, explaining buoyancy.

3. The Sand Reckoner (The Arenario):

   • Archimedes addressed the question: How many grains of sand fit in the universe?

   • He calculated: 1 grain of sand=1/10,000 of a poppy seed grain and 1 poppy seed grain=1/40 of a finger which is 1/10,000 of a stadium (100m). The universe is a solid sphere of radius

     Using these ratios, he estimated the universe's volume as a solid sphere and estimated 10^51 grains of sand

4. Measurement of the Circle:

Archimedes developed a method to approximate the circumference a circle C and pi by inscribing and circumscribing polygons around the circle. He showed that : P_n<C<P_2n where P_n is the perimeter of the inscribed polygon and P_2n is the perimeter of the circumscribed polygon. Using this approach with polygons up to 96 sides, Archimedes calculated: 3+10/71<π<3+1/7

5. Spirals:

   • Worked with the Archimedean spiral, describing the trajectory of a point moving outward from the origin at a uniform rate while the angle increases uniformly.

   • He linked the spiral to problems like angle trisection and circle squaring.

Specific Problems and Results:

Trisection of an Angle:

1. Divide the radius-vector OP into three equal parts.

2. Draw a circle with radius (1/3)OP

3. The intersection of the circle with the spiral determines a new radius-vector OQ, forming an angle that is 1/3 of the given angle.

Squaring the Circle:

1. Given a point PP on the spiral, the arc length of the circle with radius OP equals the segment OQ, where Q is the intersection of the tangent to the spiral at P and the perpendicular to OP through O.

Parabolas:

Archimedes worked on calculating the area of a parabolic segment, the region bounded by a parabola and a straight line. Archimedes proved that the area of the parabolic segment is 4/3

Archimedes proved:

The volume of a sphere is 2/3 the volume of the cylinder that circumscribes it.

A cone’s volume is one-third the volume of the cylinder that has the same base and height

Apolonio de Perga

(262-190 BC)

Apollonius worked at the museum of Perga, which had a large library, though not comparable to that of Alexandria. It is believed that Apollonius travelled to Alexandria to study.

Although most of his works have been lost, we still retain the following:

• Tangencies: Apollonius tackled what is now known as the problem of pollonius: given three elements (points, lines or circles), determine a circle tangent to the given line and/or circles and passing through the points. This problem was not solved until the 17th century.

• “Conics” composed of 8 books (of which only 7 survive), contains important results related to conic sections:

  • finding the tangents to an ellipse from an external point

  • determining a tangent line passing through a point P on the ellipse. consider the diameter passing through P (a segment joining P to the ellipse). He analysed the parallels and their midpoints, forming another diameter (called the conjugate diameter) that is parallel to the tangent at P

  • Apollonius studied the relationship between a diameter of a conic section (ellipse or hyperbola) and its conjugate. He observed that the points on one diameter correspond symmetrically to the points on its conjugate. When the diameter is shifted to pass through the vertex of the conic, this symmetry and the relationship between the two diameters remain consistent. This allowed Apollonius to explore properties specific to ellipses, hyperbolas, and parabolas, connecting their geometric characteristics.

  • These curves were originally called sections, because they were obtained by slicing a cone with a plane.

  • When sections are perpendicular, Apollonius showed in Book 1 how to construct sections with more angles and even sections of double-napped cones.

La astronomía de Claudio Ptolomeo. Comparación con el trabajo de Copérnico, Galileo y Kepler

Claudius Ptolemy (100-170 AC) worked in the library of Alexandria, developing an astronomical theory that remained a reference until the renaissance. Among his works, we highlight

• Geography: describes the geography known to the Greeks, with a world map used until the 15th-16th centuries. He used a considerably smaller R as earth’s radius than his contemporaries and it was less accurate. Columbus later used his maps to help navigate but this miscalculation made him underestimate the size of the atlantic ocean

• The Almagest: it was preserved through arabic tradition and it provides the Ptolemaic model of the universe. It consists of 13 books, specifically providing us with trigonometric tables, star and constellation charts, and an explanation of the Egyptian model of the solar system.

  Trigonometric tables: For angles from 0-180 with increments of 1/2. Ptolemy’s work relied on the geometric properties of circles and chords rather than the triangle-based trigonometry used today.

• Star and constellation tables: lists 1022 objects

• Ptolemy argued that the Earth was a sphere in the center of the universe, from the simple observation that half the stars were above the horizon and half were below the horizon at any time (stars on rotating stellar sphere), and the assumption that the stars were all at some modest distance from the center of the universe

  In the Ptolemaic system, each planet is moved by a system of two spheres: one called its deferent; the other, its epicycle. The deferent is a circle whose center point, called the eccentric and marked in the diagram with an X, is distant from the Earth. The original purpose of the eccentric was to account for the difference in length of the seasons (northern autumn was about five days shorter than spring during this time period) by placing the Earth away from the center of rotation of the rest of the universe. Another sphere, the epicycle, is embedded inside the deferent sphere and is represented by the smaller dotted line to the right. A given planet then moves around the epicycle at the same time the epicycle moves along the path marked by the deferent. These combined movements cause the given planet to move closer to and further away from the Earth at different points in its orbit, and explained the observation that planets slowed down, stopped, and moved backward in retrograde motion, and then again reversed to resume normal, or prograde, motion.

• By the 15th century, geometric discoveries cast doubt on Ptolemy’s results: Nicolas Copernicus (1473-1543) proposed a heliocentric model in “de revolutionibus orbium coelestium” based on greek heliocentric models and 8 cosmological principles. Said that the earth and other planets instead revolve around the Sun. The copernican system was no more accurate than ptolemy’s system because it still used circular orbits.

• Galileo Galilei (1564-1642) challenged the classical view of fixed, immovable stars and supported perfect spheres. He made a detailed observation by telescope of the moon and described mountains on the Moon, sunspots, the phases of Venus and 4 satellites that orbited around Jupiter. This was a significant claim as it would mean not only that everything revolved around earth as stated in the ptolemaic model,but also showed a secondary celestial body could orbit a moving celestial body, strengthening the heliocentric argument that a moving earth could retain the moon. Galileo defended heliocentrism, but the Inquisition sentenced him to house arrest.

• Johannes Kepler (1571-1630): resolved the planetary motion crisis: in mysterium cosmographicum he introduced elliptical orbits and demonstrated their precision in explaining heliocentricism. In astronomia nova he established what are now known as kepler’s laws of planetary motion. However, the proof of these laws would not come until Newton. Kepler only experimentally verified them.

  1) The orbit of a planet is an ellipse with the Sun at one of the two foci.

  2) A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.

  3)The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.

  He was the first astronomer to successfully predict a transit of Venus for the year 1631

La matemática china (no hace falta desarrollar al detalle las cuentas del Teorema chino del resto)

The earliest written texts date back to around 1800 BC. The numbering system was base 10 and additive. By the 3rd century BC, during the Qin Dynasty, the first emperor ordered the burning of all books, leaving few earlier records intact.

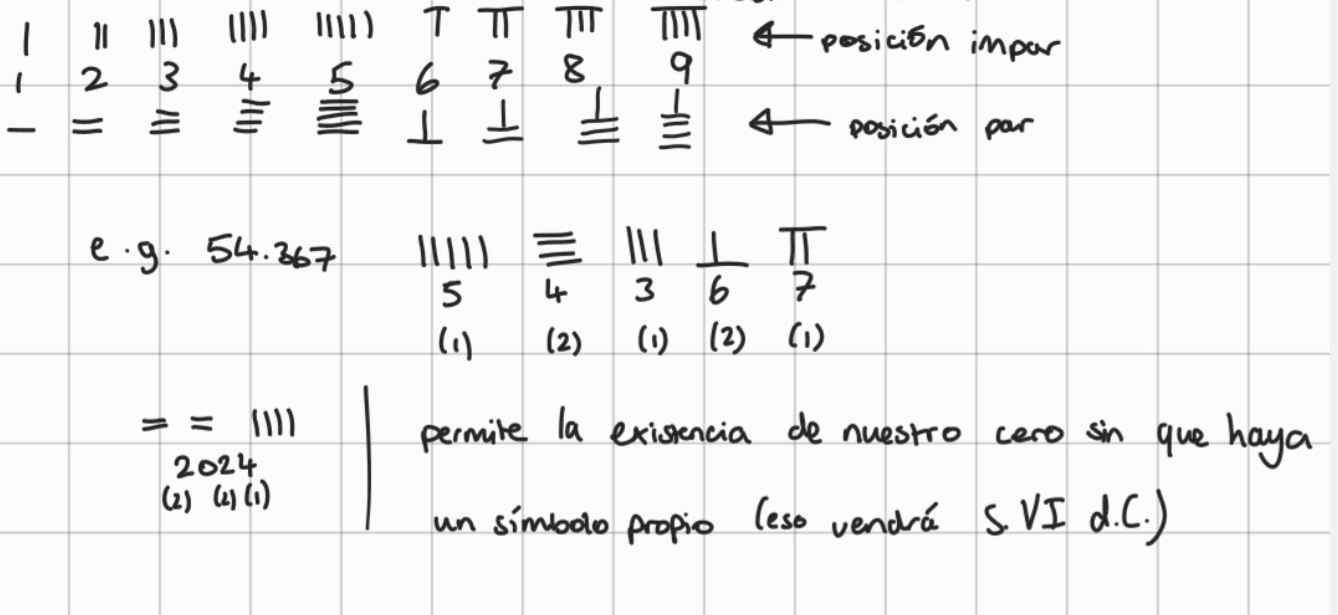
• Chinese number system: the chinese rod numeral system was used. base 10 system. positional notation: odd positions: represented numbers with vertical bars, even positions: represented numbers with horizontal bars. each digit is represented using rods in its respective positional place. The system allowed for a placeholder for zero even before the adoption of a symbol for zero (which didn’t appear until the 6th century AD).

• Zhou Bi (The Gnomon Treatise): The first Chinese mathematical book. Collected problems from the first millennium BCE. Covered geometry, arithmetic, and demonstrated proofs, including a version of Pythagoras’ Theorem (Gou Gu Xian).

• "The Nine Chapters on the Mathematical Art": An anonymous work from 200 BCE. Contains 246 problems related to areas, volumes, accounting, equations, and roots. Introduces systems of equations (e.g., 3×3, 4×4,5×5) and solutions using Gauss' method of approximations.

  Includes approximations of π:

  263 CE (Liu Hui): π=3.14159 (approximation for a 3072-sided polygon).

  480 CE (Zu Chongzhi): π=3.1415926<π<3.1415927

• The Master Sun's Manual: A work from the 5th century CE. Contains the first appearance of the Chinese Remainder Theorem.

• "The Jade Mirror of the Four Unknowns":

  Written by Zhu Shijie in 1304 CE.

  Introduces a method called the "Pascal triangle" and combinatorial properties.

  Utilized Newton’s Binomial Theorem and solved equations up to 14th degree (providing both exact solutions and excellent approximations).

La casa de la sabiduría de Bagdad y la obra de al-Juarismi

The Arab society of the 8th century stands out for its respect for culture: they assimilated the knowledge of the territories they conquered. So much so that in 803, the caliph Al-Mamun created the House of Wisdom, a cultural center located in Baghdad, the capital established by the Abbasid dynasty. The house of Wisdom, in addition to being a center for studies, contained a huge library. This lasted until it was destroyed in 1258 by the Mongols but many works by important mathematicians have been stored and preserved:

• Mohamed ibn Musa Al-Khwarizmi (780-850). He moved to Baghdad, where he wrote:

  • Zij al-Sindhind: an astronomical manual that is based on Indian sidereal tables. These are astronomical tables that provide data about the positions, motions and periods of celestial bodies, specifically referencing their movement relative to fixed stars. They contain planetary positions, lunar and solar movements and periodic patterns. These tables were used to aid in navigation, predict celestial events and align religious and agricultural calendars with astronomical cycles. Additionally, trigonometric tables appear, which give rise to the word sine.

  • De aloritmi de numero Indorum: a treatise on arithmetic manipulations in the indian numbering system, for which we only retain copies in latin

  • Hisab al-jabr wal-muqabalah (820 BC): Widely considered the first systematic treatise on algebra. It’s name means “compendium of restoration and balance”. Restoration (al-jabr) consist os moving a term to the other side of an equation by adding it. Balance (al-muqabalah) refers to cancelling out equal terms on both sides of the equation. Since the format of the work is more of a manual, it was likely used in the House of Wisdom as study material, for example, on second-degree equations. In these, the word “jidr”=”root” is used to denote the unknown. It stands out that, although irrational solutions are admitted, only positive values are used, both in coefficients and in solutions. There are also proofs, mainly geometric and based on completing squares. This word had an enormous impact in the arab world and later in Europe. Proof of this is that the title al-jabr gave rise to our word algebra.

La Mécanica desde Aristóteles a la Edad Moderna. Evolución hasta las leyes de Newton incluídas.

• Medieval physics focused primarily on dynamics, the study of the description of motion and its reason for being. We find that since Classical Greece, this was a topic theorised about: Aristotle (384-322 BC) developed a theory of dynamics. In it, he expressed, in line with his philosophical thinking, that motion reflects a being's natural tendency to move toward its essential nature. He discussed forces—those that cause motion and those that resist or prevent a return to this natural state. According to him, the balance of forces is manifested in velocity: if F is the force, v the velocity and R the resistance: F=v/R. He thought objects move according to their "natural tendencies." heavy objects (like stones) naturally fall downward toward the Earth, while light objects (like smoke) rise upward toward the heavens.

  This motion was thought to be inherent to the object's "substance" or "essence." He didnt ocunt for friction or inertia. Today we know that this reasoning is wrong. Over the course of history, this theory has been improved.

• In the 12th century, Averroes stated that v=k(F-R), where k is a constant.

• Bradmerdine in the 13th century said that b=kln(F/R).

• In the 13th century, the first result that worked with modern dynamics appeared: Merton’s theorem: a body moving with a uniformly accelerated motion covers the same distance in a given time as a body moving for the same duration with a uniform speed equal to its mean speed.

• However, the elimination of aristotelian thought would not arrive until Galileo Galilei. The New Sciences was published in 1638 and is considered one of the foundational texts of modern physics, it focuses on two main topics:

  1. Strength of Materials

  exploring concepts like:

  • The behavior of materials under stress and strain.

  • Why structures of certain shapes or sizes can withstand forces better than others.

  • The relationship between the size of an object and its ability to support its own weight, introducing the square-cube law (strength depends on cross-sectional area, while weight depends on volume).

  2. Motion and Dynamics

  • The laws of uniformly accelerated motion, laying the groundwork for classical mechanics.

  • Free fall and the insight that objects fall at the same rate regardless of mass (neglecting air resistance).

  • Parabolic trajectories of projectiles, which combine constant horizontal velocity with uniformly accelerated vertical motion.

  • Galileo refuted long-held Aristotelian ideas, such as the belief that heavier objects fall faster than lighter ones.

  • He demonstrated that mathematical principles could accurately describe physical phenomena, ushering in the era of mathematical physics.

  • Foundation of Kinematics:

    • His work on motion paved the way for Newtonian mechanics, especially concepts like inertia and the mathematical treatment of acceleration.

• Isaac Newton’s work Philosophiae Naturalis Principia Mathematica (published in 1687), which laid the foundation for classical mechanics, marked a turning point in the development of dynamic theory and established a framework that shaped modern physics. In this groundbreaking text, Newton formulated the three laws of motion, which remain fundamental to physics today:

1. An object at rest remains in the same state of motion unless a resultant/external force acts on it

2. F=ma

3. For every action, there is an equal and opposite reaction.

Beyond these, Newton made profound contributions to gravitational theory, describing the universal law of gravitation. He demonstrated that every particle in the universe attracts every other particle with a force proportional to the product of their masses and inversely proportional to the square of the distance between them:

This law provided the theoretical framework to explain phenomena such as planetary orbits, the motion of moons, and tides. Newton used this theory to mathematically prove Kepler’s laws of planetary motion, which describe the elliptical orbits of planets around the Sun.

El álgebra en el Renacimiento: Cardano (en particular, no hay que saberse las expresiones concretas de las ecuaciones de grado 3 y 4, pero sí cómo deducirlas y las consecuencias)

The Renaissance, a period spanning the mid-15th to the 17th-century, is characterised by significant artistic changes with an emphasis on perspective, geographical changes linked to the first wave of globalisation, and cultural changes with the use of Latin languages and the invention of the printing press. Thanks to the printing press, the dissemination of texts grew notably, particularly mathematical texts, which revealed a growing interest in astronomy and algebra.

One of the greatest algebraic contributions is by Gerolamo Cardano (1501-1576) an engineer, physician and mathematician who wrote:

• Liber de ludo aleae: describes the probabilistic concepts as a way to measure risk in games

• Ars magna: the first formula for the solution of cubic equations and with demonstrations (both geometric and algebraic). He uses the formula x=p+-sqrtq, r, and the hindu-arabic numerical system. He looks for solutions (which may be irrational or positive), and he divides cases based on whether the coefficients are positive

• Cardano credits the formula to Tartaglia and Scipione del Ferro. Method: Cardano's method for solving cubic equations works like this:

  • Start with normal cubic

  • simplify using a variable substitution which eliminates the quadratic term so u get a DEPRESSED CUBIC: z³+pz+q=0 where p and q depend on the original coefficients

  • the roots z1, z2, z3 of the new equation satisfy z1+z2+z3=0

  • Introduces 2 new variables u and v with the conditions u-v=z and uv=-p/3. a quadratic equation in terms of u³ or v³ is derived and as u and v are related to the roots z, we can solve for u and v to find z.

  • he also analyses the discriminant and finds to find the number of roots and in doing so discovers cases where the the expression under the square root is negative

• Situation marks the birth of complex numbers

• Cardano credits Luis Ferrari, a student of his, for solving quartic equations. The reasoning is analogous to cubic equations, with an additional variable change to reduce the degree of the equation. Ferrari’s method solves quartic equations, introducing roots of negative numbers despite the existence of real and positive solutions.

El trabajo de P. de Fermat

Pierre Fermat (1605-1661) was a French lawyer who engaged with mathematical questions outside of his professional life. For this reason, his works were not published until 1679 when, after his death, they were organised and published in the following manner:

• Using analytic geometry before Descartes, he was able to reduce Apollonius’ problems concerning conics to equations involving distances of lines and points.

• He sought maximums, minimums and tangents to polynomial functions. For maximums and minimums, he built on Keplers idea that at a critical point, the following holds: (P(x+A)-P(x)/A=0, by taking A=0 after performing the operation. Although this method (predating the concept of derivatives) does not apply in all cases, it works for polynomials. It was also used to find the tangent line at a point. Another idea related to differential calculus was calculating the area under the curve y=x^n between 0 and 1. To do this, Fermat approximated the curve using rectangles.

• We owe Fermat important results in number theory:

  He created Fermat’s primes, which are numbers of the form: 2²^^n+1 and claimed they are always prime. Although Euler demonstrated this is not true (it fails for n=5), these numbers are very important for cryptography.

• He posed a conjecture stating x^n+y^n=z^n (with x,y,z natural numbers and n>2) has no solutions. Without providing a proof, the problem remained open until 1995 when it was resolved.

La obra de I. Newton y G. Leibnitz

Isaac Newton (1643-1727) was an English scientist, while Leibniz (1646-1716) was German. Both developed, in parallel but independently, their own theory of differential calculus. This led to some tensions, which were initially amicable (newton mentions Leibniz in one of his works) but disputes soon became bitter (Newton erased all references to Leibniz in later editions, and their followers debated for decades. In fact, the mathematical community became divided. Initially, Newton seemed to have developed it earlier, but some of Leibniz’s letters show that he had the concept as well. However, comparing their two theories, it becomes clear that they were independent studies.

Newton’s contributions: Newton gathered many of his works later in life and composed some of his most notable achievements, particularly in algebra and physics. For his calculus, he introduced the concept of derivatives which he called “fluxions”. Fluxions measure quantities that depend on time (called the flux) and the incremental variation (the fluxion). He detailed this in Methodus fluxionum et serierum infinitarum (written in 1671 but published in 1736 after his death). In it he explained that if x(t) is the flux then the fluxion of x(t) is the limit as the change in t tends to 0 of: x(t0+change in t)-x(t0)/change in t. This is the same as the derivative in modern notation dx/dt. He also related this to areas: similar to Cavalieri and Fermat, he studied the area under the curve. He considered the function A(t) which represents the area of x(t) between 0 and t. He observed that A(t0+change in t)-A(t0)/change in t-x(t). Here, the fluxion of the area is the flux.

Leibniz’s contributions: Leibniz was a diplomat, so during his travels to England, he formed friendships with British mathematicians. However, Newton accused him of stealing his results during this period. In 1684, Leibniz published Nova methodus pro maximis et minimis (written in 1676) which exposed his theory. For the first time, terms like function, derivative, integral and differential equation were introduced.. He also introduced the notation df/dx, dx=f(x+dx)-f(x), where dx is the infinitely small differential. He described the rules of operation: multiplying, dividing and deriving (the product rule, quotient rule and chain rule. d(af)=ad(f), d(fg)=gd(f) + fd(g), d(f/g)=(gdf-fdg)/g². In later work, he described the area of a function and proved that: d/dx(integralsign f(x,t)dt)=f(x).His method was more algebraic and abstract than Newton’s, making it easier to apply and understand. Was more accessible and influential.