Game Theory - Normal Form, Rationality, Dominance

Normal Form Game

Strategy profile

Payoffs and Rationality

The payoff function should associate utility to each strategy profile

• Rational players therefore maximize their expected utility.

• Any risk-aversion is already incorporated into the payoff; expected utility is linear in probabilities.

Not only are all players rational, but rationality is common knowledge

• Everyone knows everyone else is rational

• Everyone knows everyone knows everyone else is rational

• And so on, forever

Payoff Matrices

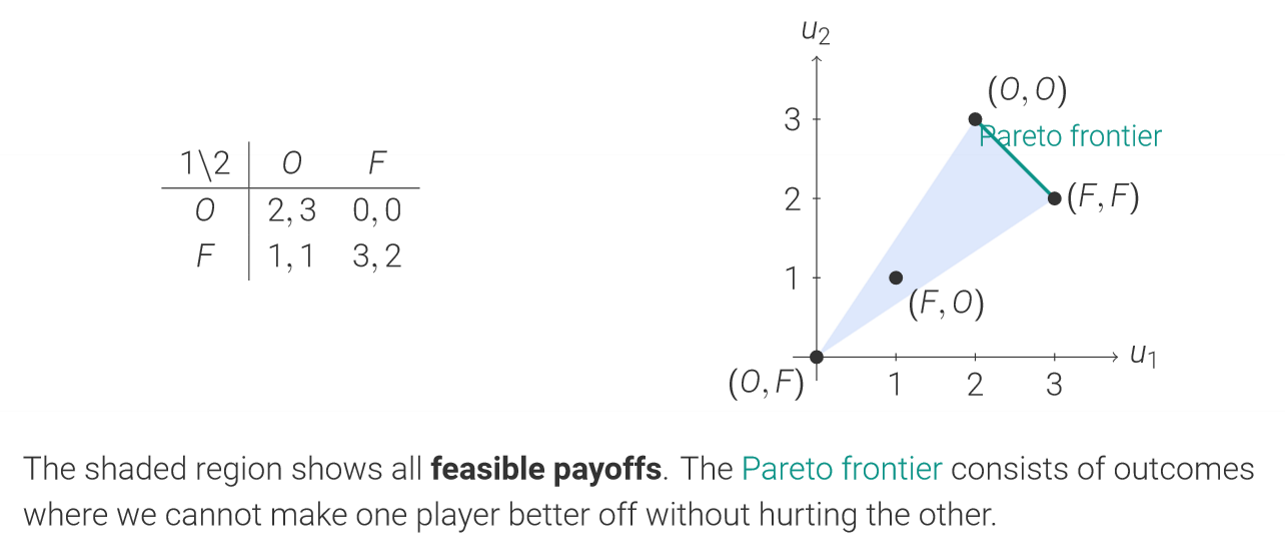
Feasible Payoffs and Efficiency

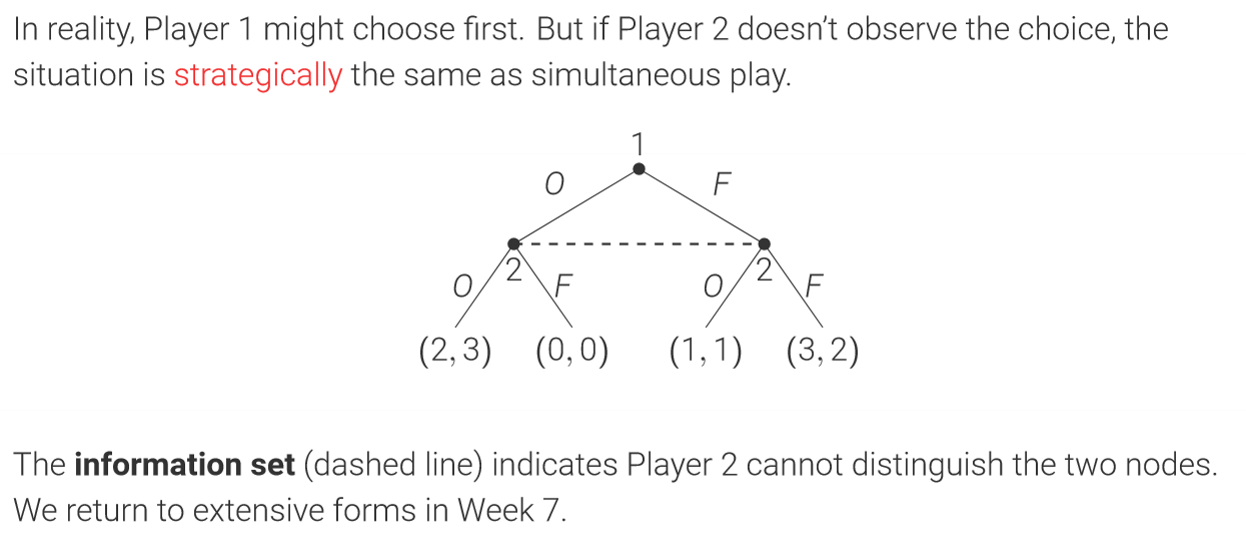
Extensive Form

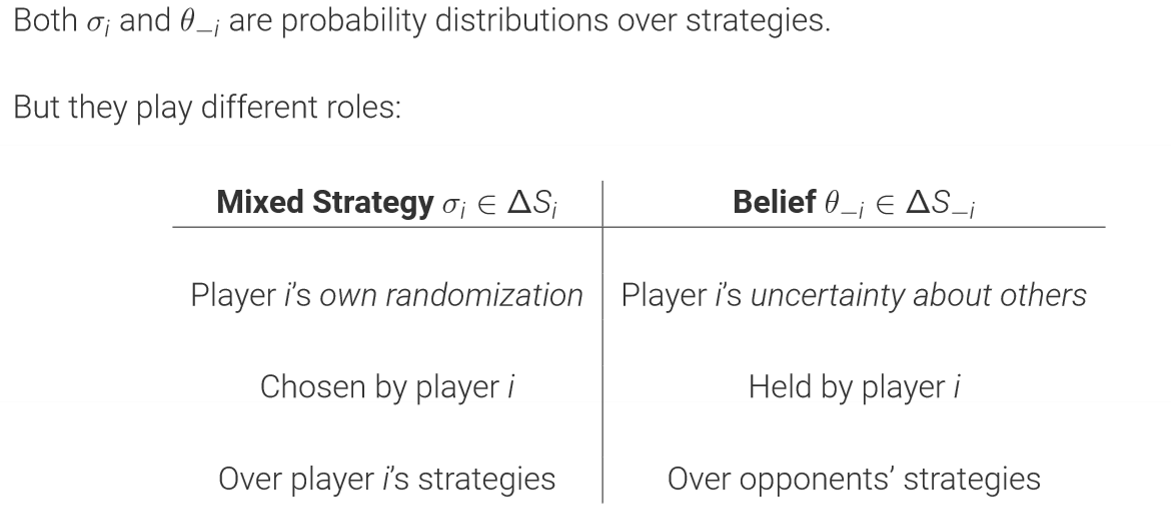
Mixed strategy

Pure strategy

Beliefs

Beliefs vs Mixed Strategies

Expected Payoff Given Beliefs

Best Response (Pure)

Mixed Strategy Best Responses

Dominated Strategies

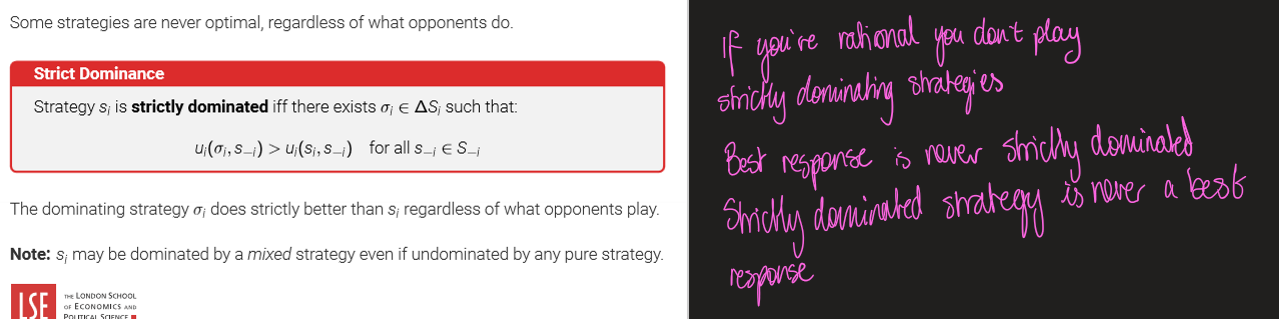
Equivalent characterisation

Dominant Strategy Equilibrium

Dominance by a Mixed Strategy

Weak dominance

Common knowledge of rationality

• A player who is rational does not play dominated strategies.

• If I know you are rational, I know you are best-responding to some belief. Thus I know you’ll never play a strategy which is never a best response.

• This restricts which beliefs I should hold, and therefore which strategies I should play.

• If you know that I know you are rational, you know I’ll never best-respond to a belief that puts weight on strategies which are never your best responses.

• This restricts the beliefs you should hold, and which strategies you should play.

• And so on...

If rationality is common knowledge, this procedure can proceed indefinitely.

The surviving strategies are called rationalizable

Iterated dominance

Dominance: Summary

Dominance is often considered a benchmark of rationality:

• Rational players never choose dominated strategies.

• Common knowledge of rationality means players only employ strategies that survive IDSDS. But dominance has important limitations:

• Often there is no dominant strategy, even after iteration.

• It often leads to inefficient outcomes (recall Prisoner’s Dilemma). A weaker notion of equilibrium is needed, especially for richer setups: Nash Equilibrium

Common Knowledge of Rationality

IDSDS relies on common knowledge of rationality:

• All players are rational.

• All players know all players are rational.

• All players know all players know all players are rational.

• And so on, ad infinitum.

The Beauty Contest illustrates that this is a strong assumption.

Even if you are rational, you may not want to play as if everyone else is.

Summary:

Normal form game

Mixed strategies

Beliefs

Best response

Strict dominance

IDSDS