A level further maths 6

Modulus argument form of imaginary numbers

z= r(cos¥+isin¥)

Matrix multiplication for 2×2

First row x first column= top left

First row x second column = top right

Second row x first column = bottom left

Second row x second column = bottom right

Matrix size

Rows x columns

For multiplying, a (2×3)(3×2) will leave 2×2 as the inner two numbers cancel out

Identity matrix

1 0

0 1

I2 x any 2×2 matrix leaves it to be itself

Inverse matrix

1/determinant (top left and bottom right switch places, top right and bottom left switch signs)

Roots of polynomial facts

ą+ß= -b/a

ąß=c/a

and keeps increasing with increasing orders of polynomials

Singular matrix

Determinant= 0

If a matrix is singular, the inverse doesn’t exist

Invariant lines

Lines of invariant points

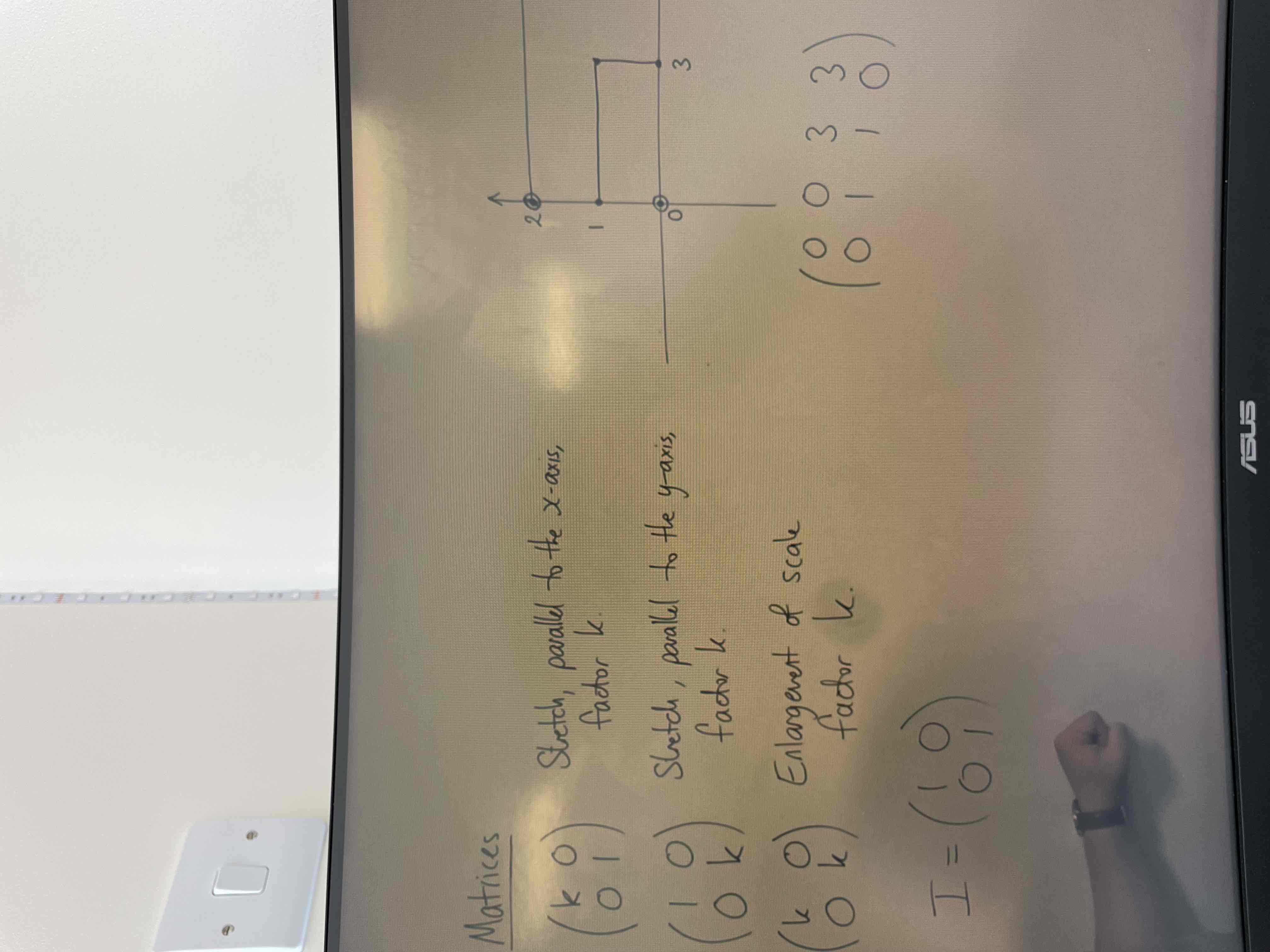
Matrix transformations

General formula for a reflection in the line y=(tan¥)x

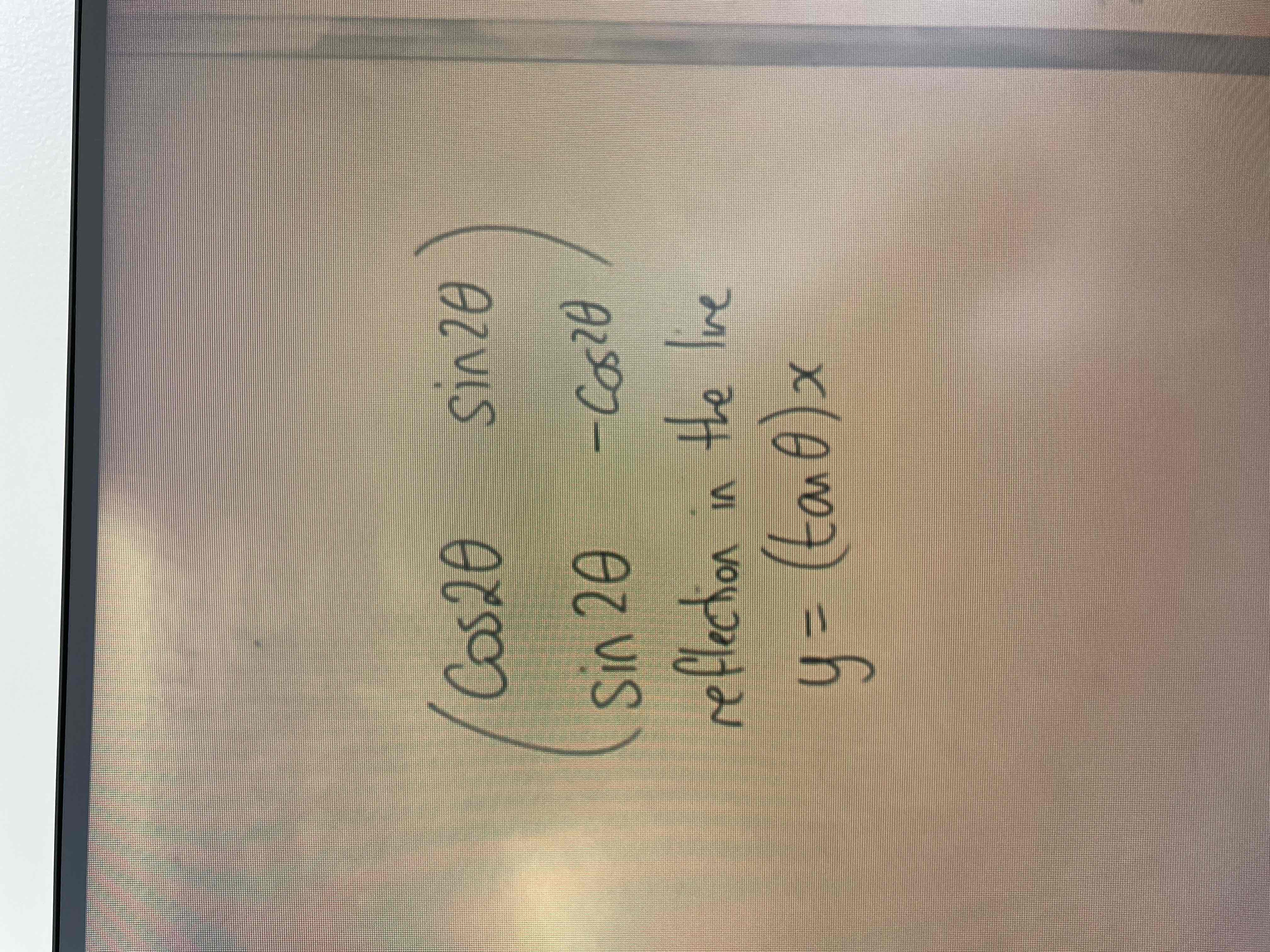
Reflective matrices

Rotational matrices

Rotation by certain angle

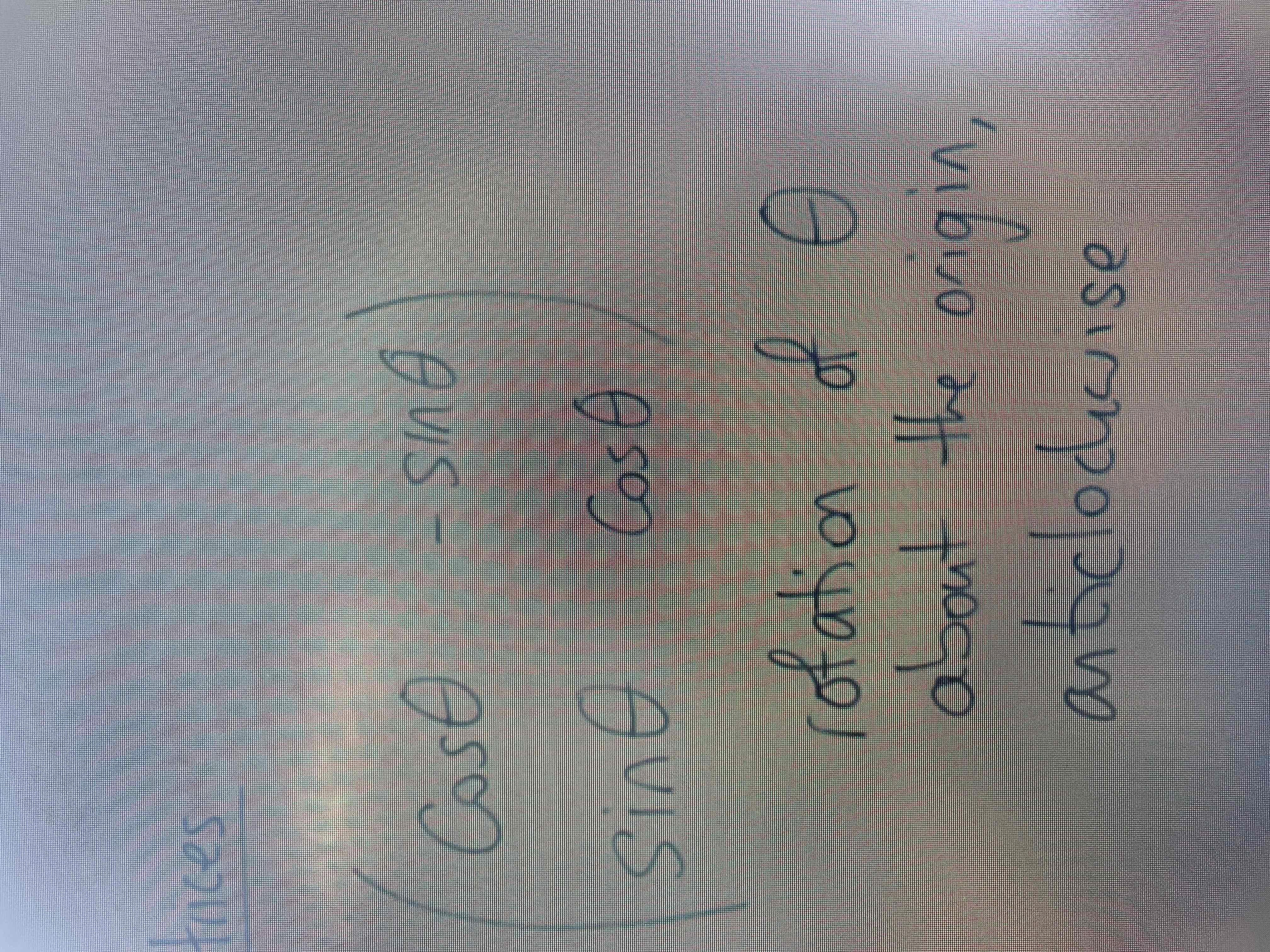
Shears

Points on the x axis remain fixed and all others move

Points below x axis move to the left, points above the x axis move to the right

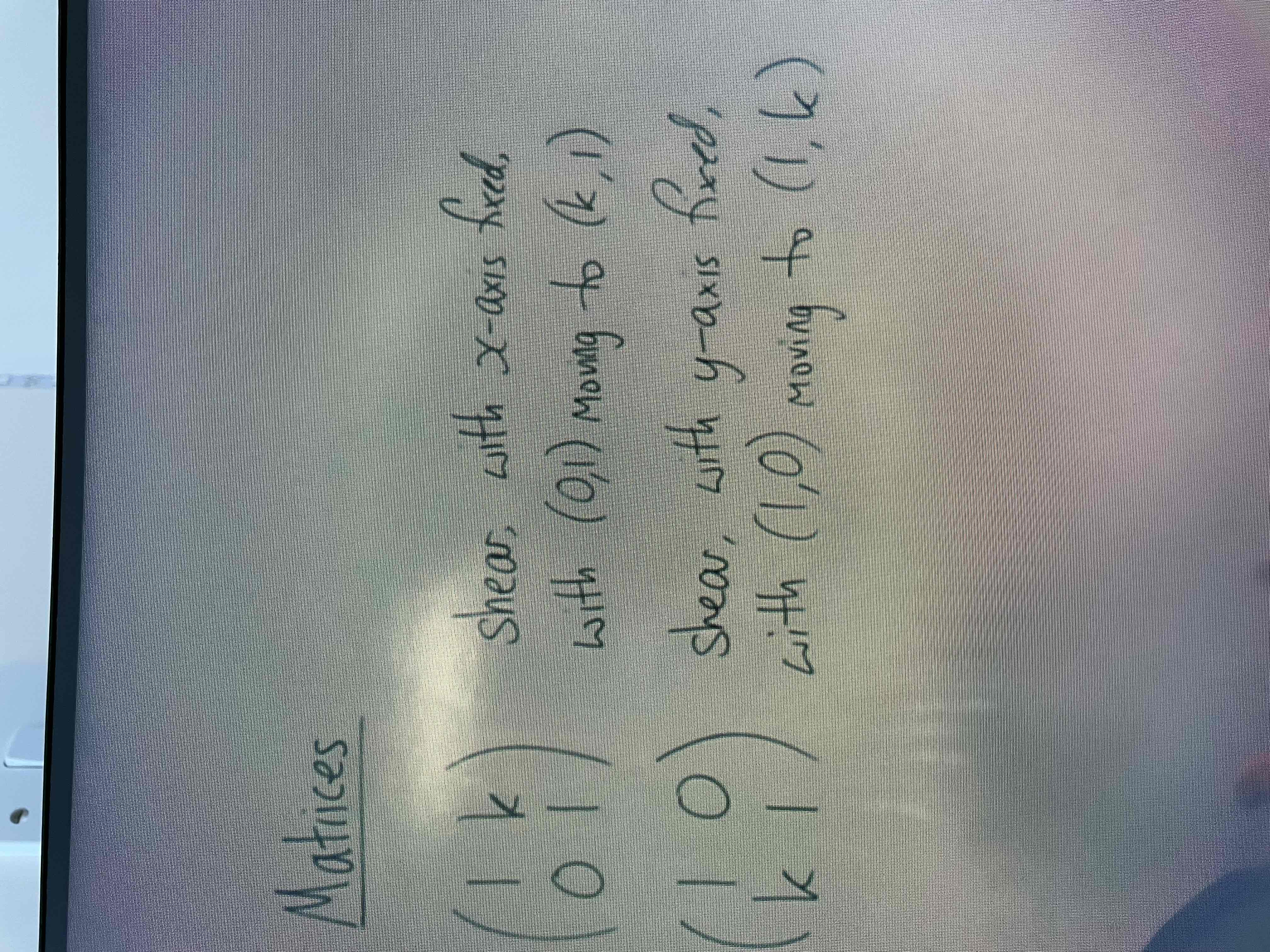
3D matrices for stretches and enlargement of certain axis

3D rotations about a given axis by an angle ¥

Solving simultaneous equations using matrices

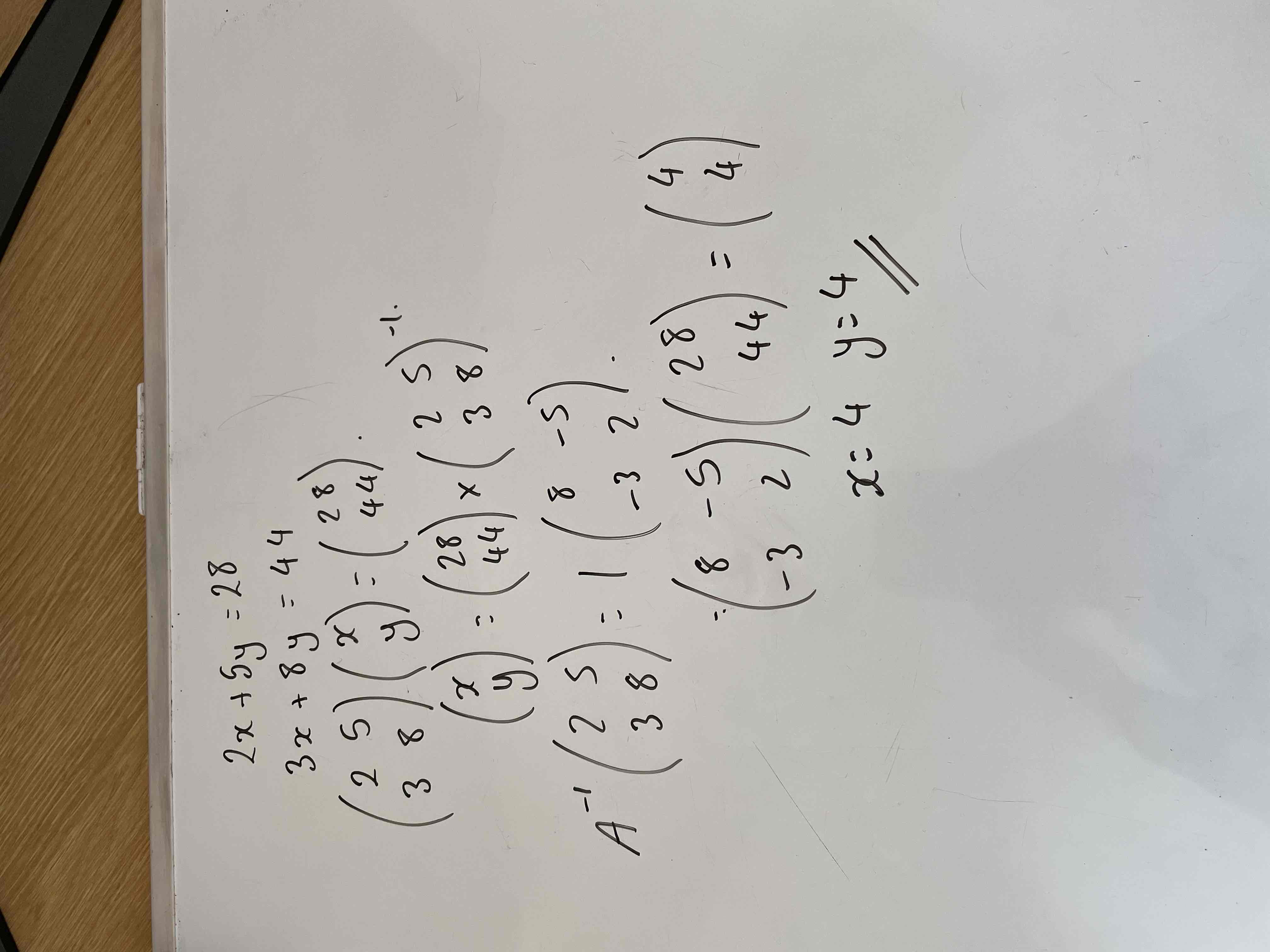
How to determine whether a simultaneous equation has a solution

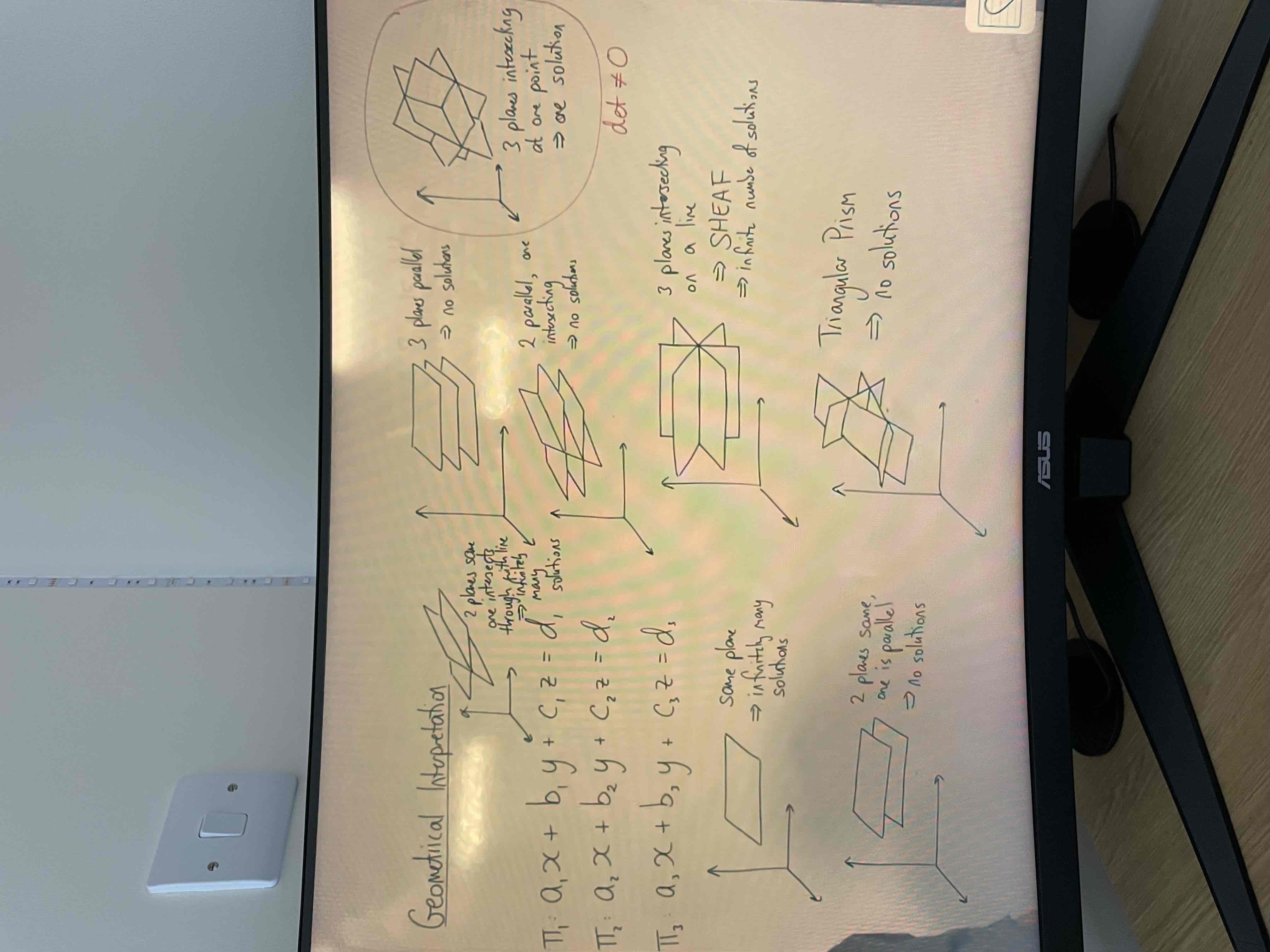
3D geometrical interpretations

General vector equation for 2D

OA + (lambda) AB

Vector: scalar product

Using cosine rule with the magnitude of the vectors

For 3D vectors, cos¥= a • b/ |a| • |b|

If perpendicular, dot product = 0

Inverse of 3×3 matrix 4 steps

DMFT

De moivres theorem

z=re^i¥

Finding the angle between a line and a plane

ALWAYS USE THE SCALAR PRODUCT

Intersecting vectors

Line and plane intersection

Split up into xyz and then sub in

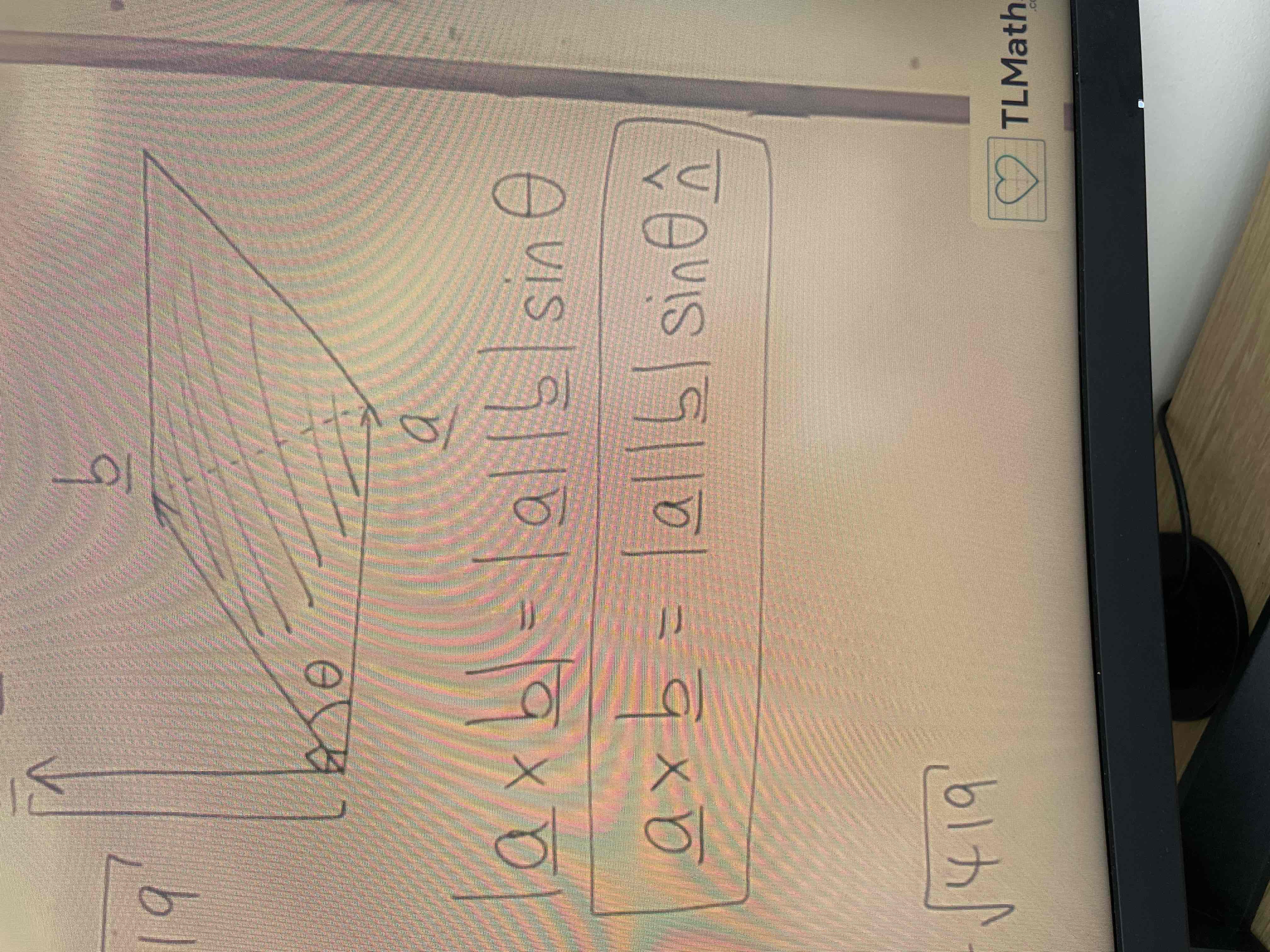
Vector product

Produces a vector that is perpendicular to the vectors that create it

Given formula in booklet

Vector cross product link to scalar product

Can be used to find the area of a parallelogram that connects vectors a and b

Shortest distance from a point to a line in 3d

Where P is the position vector and the line is of form r= a+¥d

Shortest distance from a line in 2D

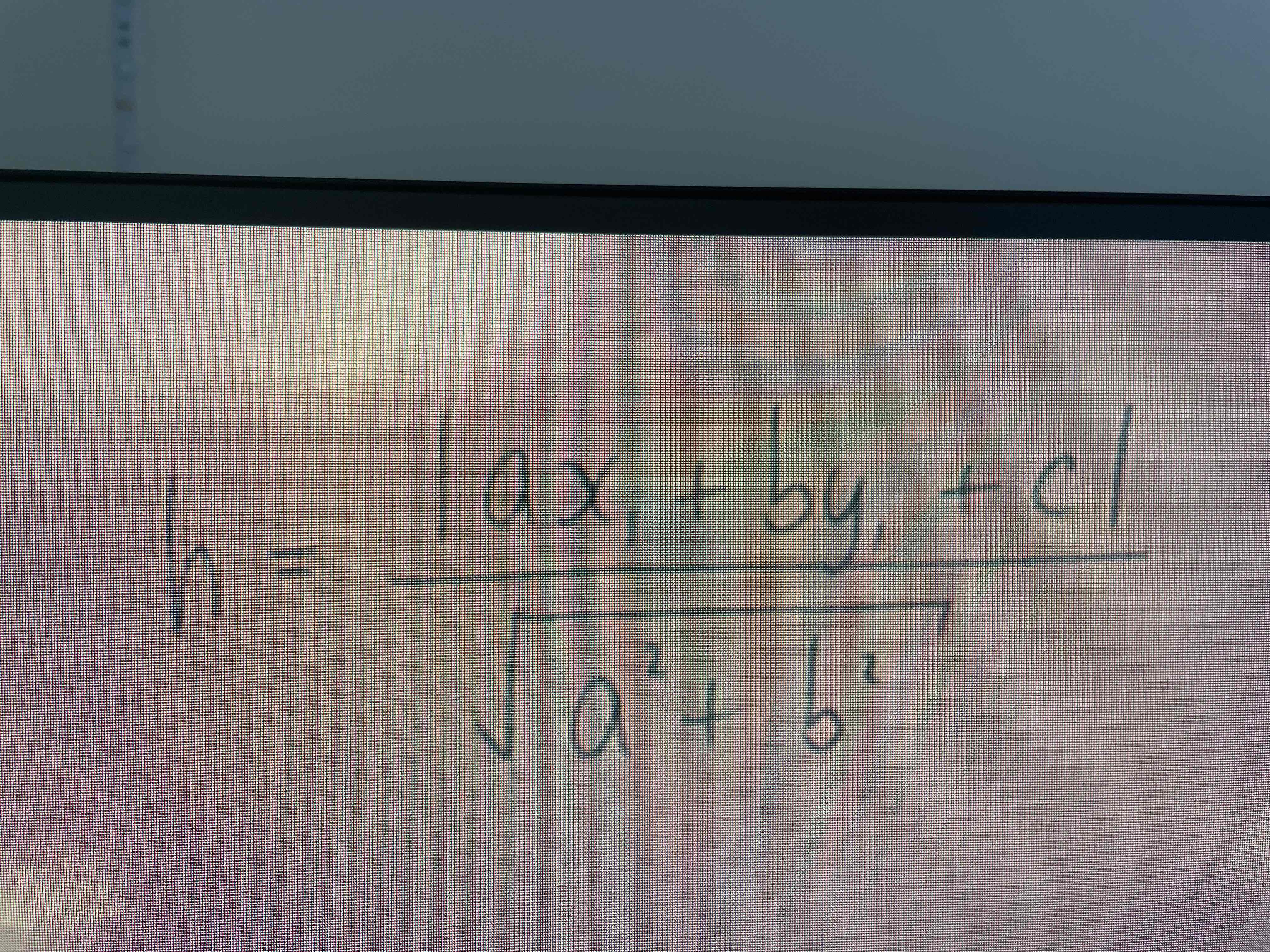
General vector equation of a 3D line

r = OA + ¥AB + (mew) AC

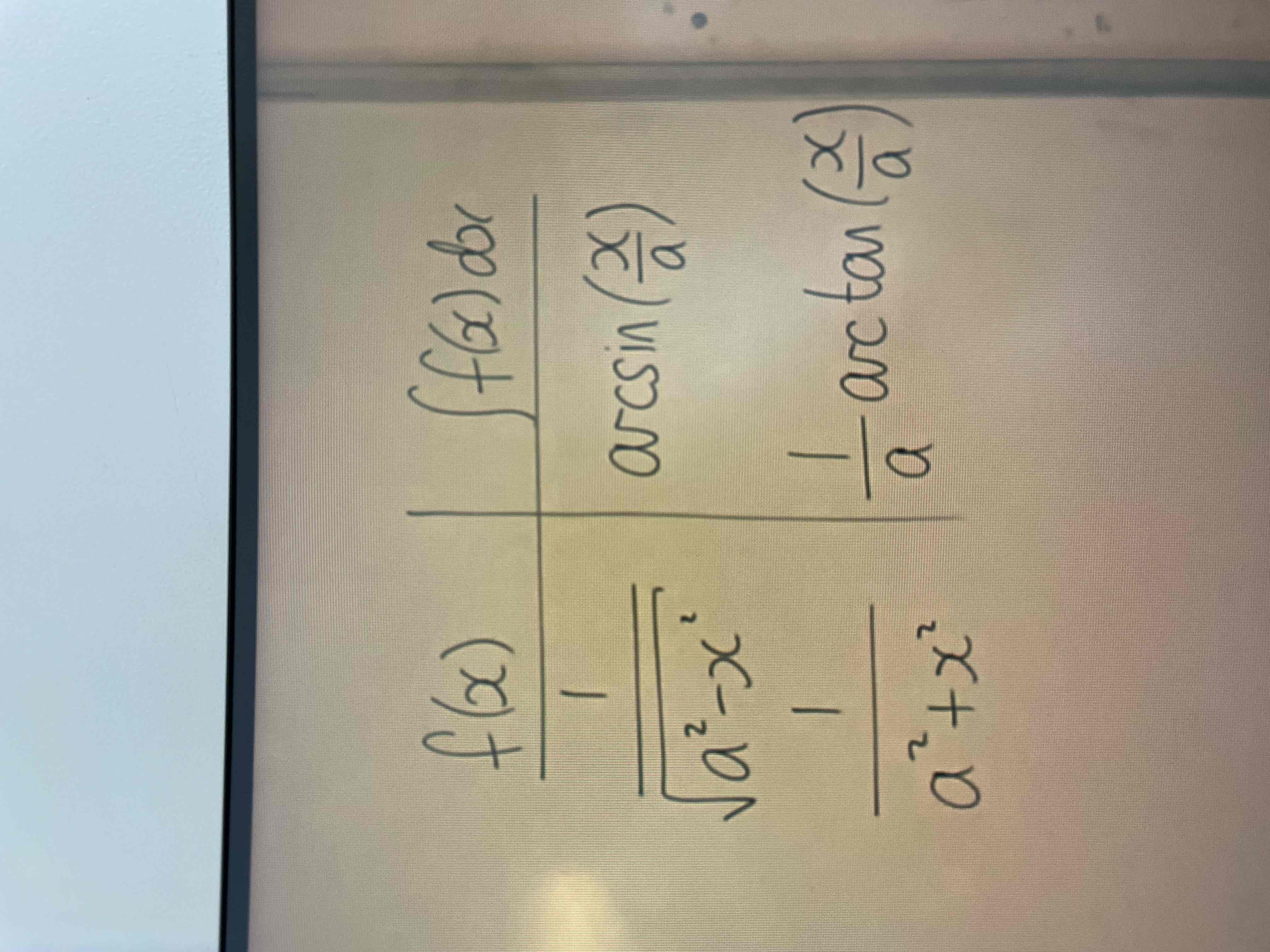
Differentiating arcsinx

Integrating to arcsinx

If a root is involved in the bottom of the fraction use substitution of x=sinu

Integrating arctanx

If there is not a root on denominator then use x=tanu

Integrating from 1/a²-x² to arctrig

Mean value formula

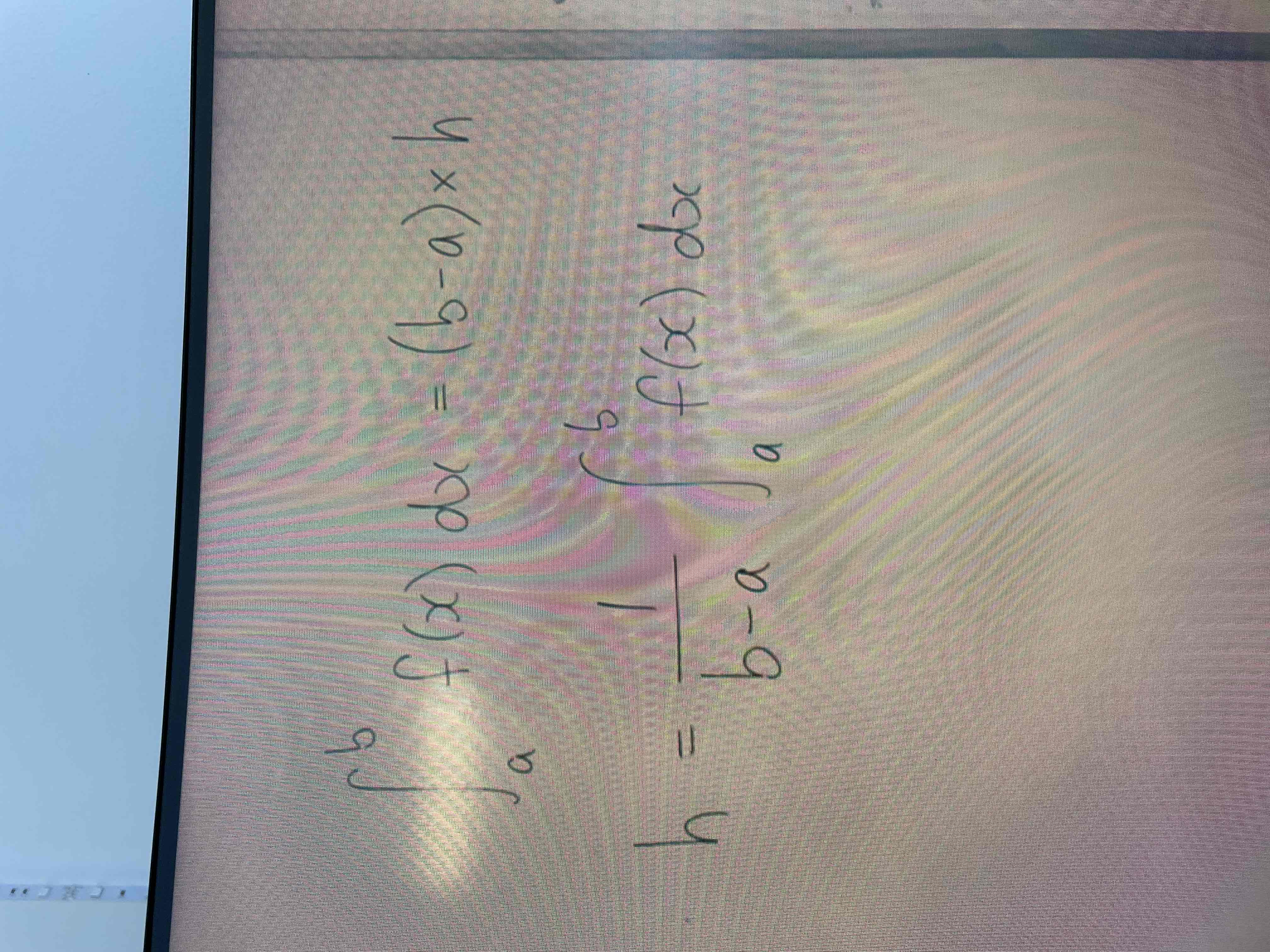
Partial fraction with quadratic factor

Hyperbolic functions in terms of e

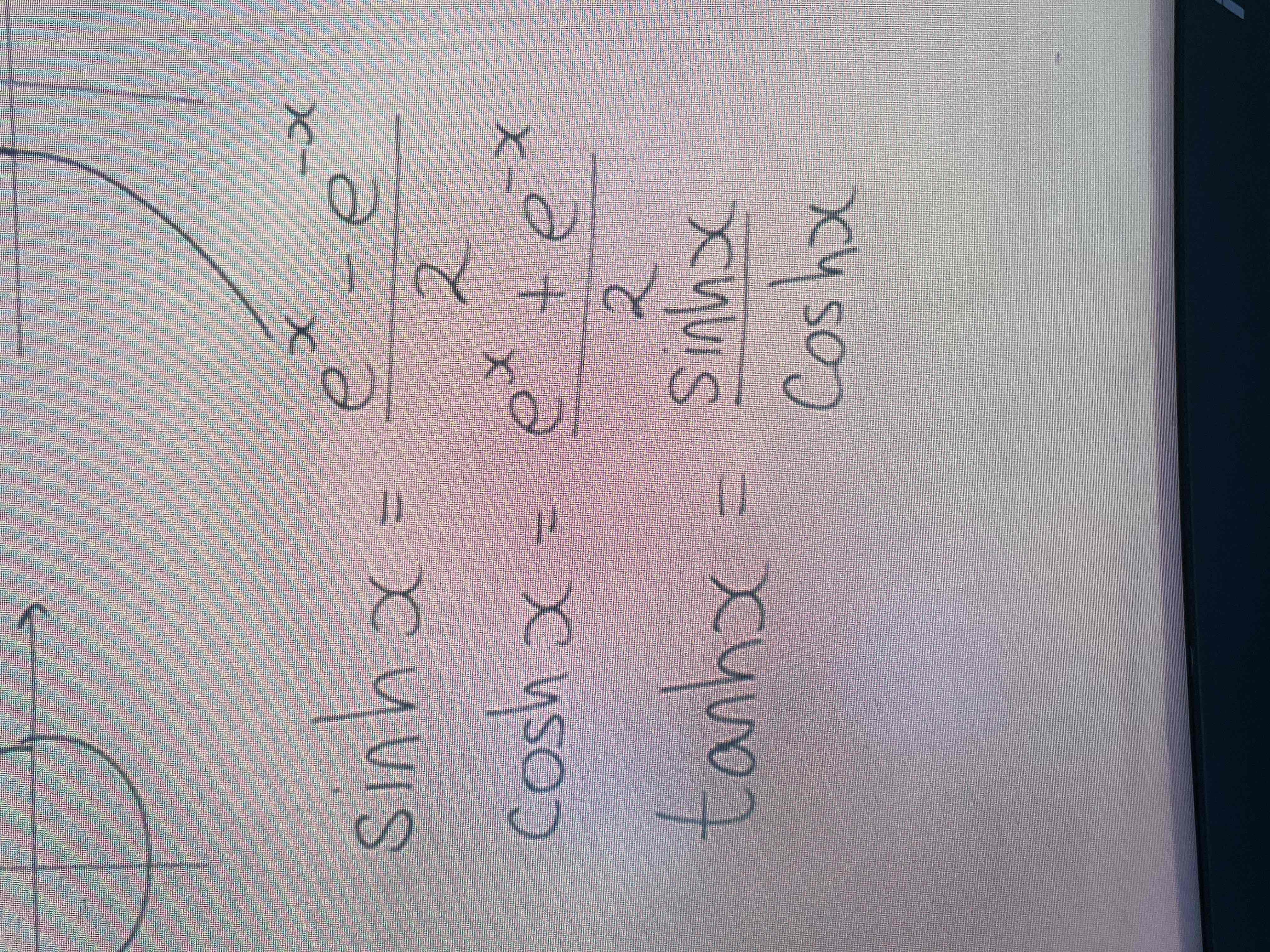
Sinhx domain range and graph

Derivatives of hyperbolic functions

sinh = cosh

cosh = sinh

tanh = sech²

coth = -csch²

Identities with hyperbolic functions

cosh² - sinh² = 1

1 - tanh² = sech²

coth² - 1 = csch²

Osbournes rule says they are identical to normal trig functions just put a negative in front every time sin²x appears

Inverse hyperbolic functions

To derive, use y= sinh^-1 then rearrange for y using quadratic formula

Differential equations forms for real and complex

Ae^(alpha)x+Be^(beta)x

Ae^(alpha)x+Bxe^(beta)x

Acos(alpha)x+Bsin(alpha)x

e^(alpha)x (Acos(beta)x + Bsin(beta)x) where complex numbers are of the form alpha+ or - beta i

System of differential equations

Solve for one variable in either x or y then sub into the other formula