Sequences and Series

sequence

list of nums written in a specific order (increasing, decreasing, exponential increase, etc), indexed with pos, natural nums

• a1, a2, a3, … an (the nums are subscripts)

notations for sequence

{a_n}, {a_n} → (infinite as superscript, “n=1” as subscript)

• unless otherwise stated, assume that n starts at 1 and goes up to infinity

finding a formula for the general term of a sequence

• observe how the numerator changes separate from how the denom changes

• use (-1)^n for alternating neg sign

graphing sequences

• input: pos natural nums (i)

• output: terms of the sequence (o)

• ex: (i, o) = (1,1/4), (2, 2/9)… given the general sequence term:

  • a_n = n/(n+1)²

if a limit of a sequence approaches a real num, the sequence is ____

convergent

if the limit of a sequence DNE (either approaches infinity or alternates between nums infinite times), the sequence _____

diverges

(limits of sequences rules)

the squeeze/sandwich theorem

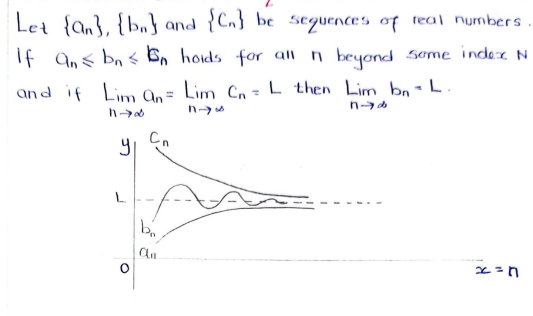
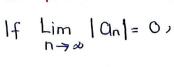
ONLY if it’s zero

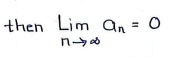
the sequence {r^n} =

monotonic sequence

a sequence that is always either increasing or decreasing

bounded sequence

a sequence where all the terms are withen a certain range (like a bounded area region)

deriv method to det if a sequence is monotone

• the deriv of the sequence fn is always pos

• the deriv of the sequence fn is ALWAYS neg (no matter what input value)

you can sometimes _________ the first few terms of a sequence and it would not change the limit of the sequence

discard

to det whether a sequence is strictly increasing or decreasing

• even if the fn fluctuates for the first few terms, it can EVENTUALLY strictly increase/decrease

• observe whether the deriv of the sequence fn f(x) is positive or negative for all x vals greater than or equal to 1

• BUT it could be x vals greater than or equal to any num greater than 1 (hence, the sequence EVENTUALLY strictly decreases/increases)

• sub in nums greater than 1 into the deriv and observe how the fn changes

if a sequence is eventually increasing, then either:

1. it has an UPPER bound that is a constant (lim exists)

2. it diverges to POSITIVE INFINITY

if a sequence is eventually decreasing, then either:

1. it has a lower bound that is a constant (lim exists)

2. it diverges to NEGATIVE INFINITY

bounded sequence cont’d

• would have an upper bound (upper lim)

• or a lower bound (lower lim)

• (basically find the lim of the sequence)

for sequences w alternating sign (-1)^n, take the lim of the __________

absolute val

series

SUM of the TERMS in a seqeunce

finite vs infinite series

• finite: first and last term is defined

• infinite: continues indefinitely → we must look at the sequence of PARTIAL SUMS (S1, S2, S3… (the nums are subcripts)) where S2 for example represents the partial sum of the first two terms in the sequence

sum of an infinite series simple example

we make an infinite sequence made up of the partial sums (see image)

• the sum is the limit of the sequence of partial sums (expression of Sn) as n approaches infinity

sequence of partial sums

• Sn = general expression for the sequence of partial sums

• up until n (on top of the sigma symbol) -. add up until the nth term

if the limit of the sequence of partial sums (Sn, diff from An) as n approaches infinity exists (meaning convergence), then

the series of the infinite sequence converges and comes up with a real sum.

• because the SUM of the series equals to the limit of the general expression of the sequence of partial sums (Sn)

if the limit of the sequence of partial sums as n approaches infinity DNE or is infinity (meaning divergence), then

the series of the infinite sequence itself diverges

geometric series

• “a” and “r” are both constant values

• the series can start with a num other than “a”

geometric series: if r = 1 (the common ratio raised to the power of n)

the series simplifies to:

a + a + a + a… = na → + or - infinity, therefore divergent

Sn = na

for geometric series: if r ≠ 1

memorize the last line

for geometric series: if -1 < r < 1, then r^n → 0 as n → infinity, therefore

a geometric series is convergent if:

|r| < 1

if |r| < 1 for a geometric series, the sum =

a/(1 - r)

a geometric series is divergent if:

|r| >= 1