4.3 Linearly Independent Sets/Bases

recap: if a set of vectors set to 0 has a nontrivial solution it is linearly ?

dependent

the set of vectors is not linearly independent if it contains the ?

zero vector

let H be a subspace of a vector space V . a set of vectors B in V is a basis for H if:

• B is a linearly independent set

• the subspace spanned by B coincides with H; that is H=SpanB

the set S = {1, t, t², … tⁿ} is called the __ __ for P_n

standard basis

• S spans P_ⁿ  because p(t) is a linear combination of the basis vectors

• S is linearly independent 

the spanning set theorem

• if one of the vectors in S (={v1,…vp}), say v1, is a linear combination of the remanining vectors in S, then the set formed from removing v1, still spans H (=Span{v1,…vp}

• If S is linearly independent, then S is a basis of H

basis for nullA

the vectors from the general solution

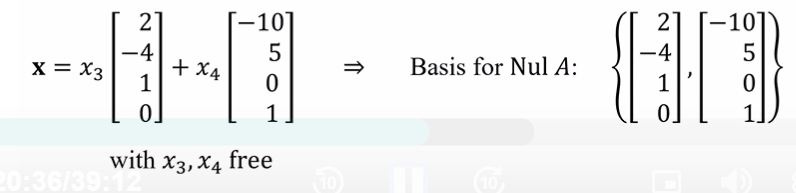
basis for colA

ONLY the pivot columns of a matrix A form a basis

• make sure it is the columns of the matrix themselves, not the reduced matrix

thm: if two matrices A and B are row equivalent then their__ __ are the same. if b is in echelon form, the nonzero rows of B form a basis for the row space of A as well as for that of B

row spaces

basis for the row space of A

the nonzero rows of the reduced matrix

if {v1, v2, v3} is a basis for R³:

• a basis is a spanning set that is as small as possible

  • if you remove a vector it is not a basis for R³

    • it is linearly independent but not span R³

• a linearly independent set is as large as possible

  • if you add a vector then it is not a basis for R³

    • it might span R³ but that is not linearly independent

(T/F) A single vector by itself is linearly dependent.

False

(T/F) If a finite set S of nonzero vectors spans a vector space V, then some subset of S is a basis for V.

True

(T/F) A basis is a linearly independent set that is as large as possible.

True

(T/F) A basis is a spanning set that is as large as possible

false

(T/F) In some cases, the linear dependence relations among the columns of a matrix can be affected by certain elementary row operations on the matrix.

False

(T/F) In some cases, the linear dependence relations among the columns of a matrix can be affected by certain elementary row operations on the matrix.

False

(T/F) In some cases, the linear dependence relations among the columns of a matrix can be affected by certain elementary row operations on the matrix.

True

A is a mxn matrix;

T/F: the column space of A = R^m so T is onto

TRUE

col(A) = range(T)

T/F: null(A) = 0 so T is one to one

true

ker(T) =0

in general, to show if vector space check if it ? the vectors

spans

range(T) is the set of all b in R^m(the odomain) such that Ax =b is ? 

consistent