Chemistry and Materials Science Final Exam

FCC

a) structure

b) number of atoms (n)

c) coordination number

d) relationship between atomic radius and lattice parameter (a)

e) along what do atoms touch?

a) 1/8 of an atom in each of 8 corners, ½ atom on each of 6 faces, ABCABCABC…

b) n=4

c) CN=12

d) a=(2√2)r

e) along the face diagonals

BCC

a) structure

b) number of atoms (n)

c) coordination number

d) relationship between atomic radius and lattice parameter (a)

e) along what do atoms touch?

a) 1 atom in centre, 1/8 atom on each vertex

b) n=2

c) CN=8

d) a=(4/√3)r

e) along the cube diagonals

Rock Salt

a) structure

b) number of atoms (n)

c) coordination number

d) relationship between atomic radius and lattice parameter (a)

e) along what do atoms touch?

a) position anions in FCC

cations: ¼ atom on each edge, one atom in the centre

b) 4 anions 4 cations

c) CN=6 (each anion is surrounded by 6 cations and vice versa)

d) a=2R(anion)+2R(cation)

e) along cube edges

NOTE: for simple cubic, they also touch along cube edges. a=2r for simple cubic

HCP

a) structure

b) number of atoms (n)

c) coordination number

a) ½ atom on the top and ½ on the bottom, 3 atoms inside, 1/6 atom on each of 12 vertices, ABABAB…

b) n=6

c) CN=12

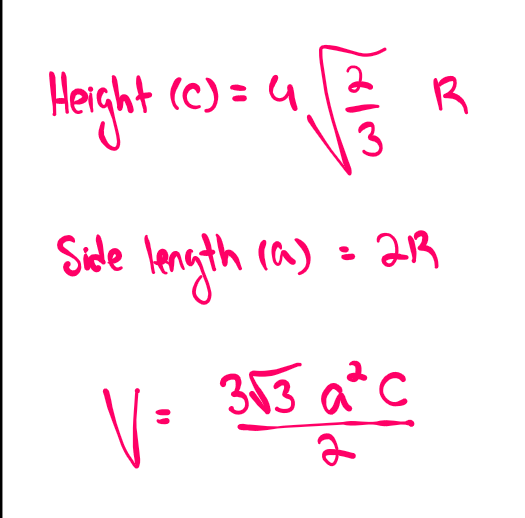
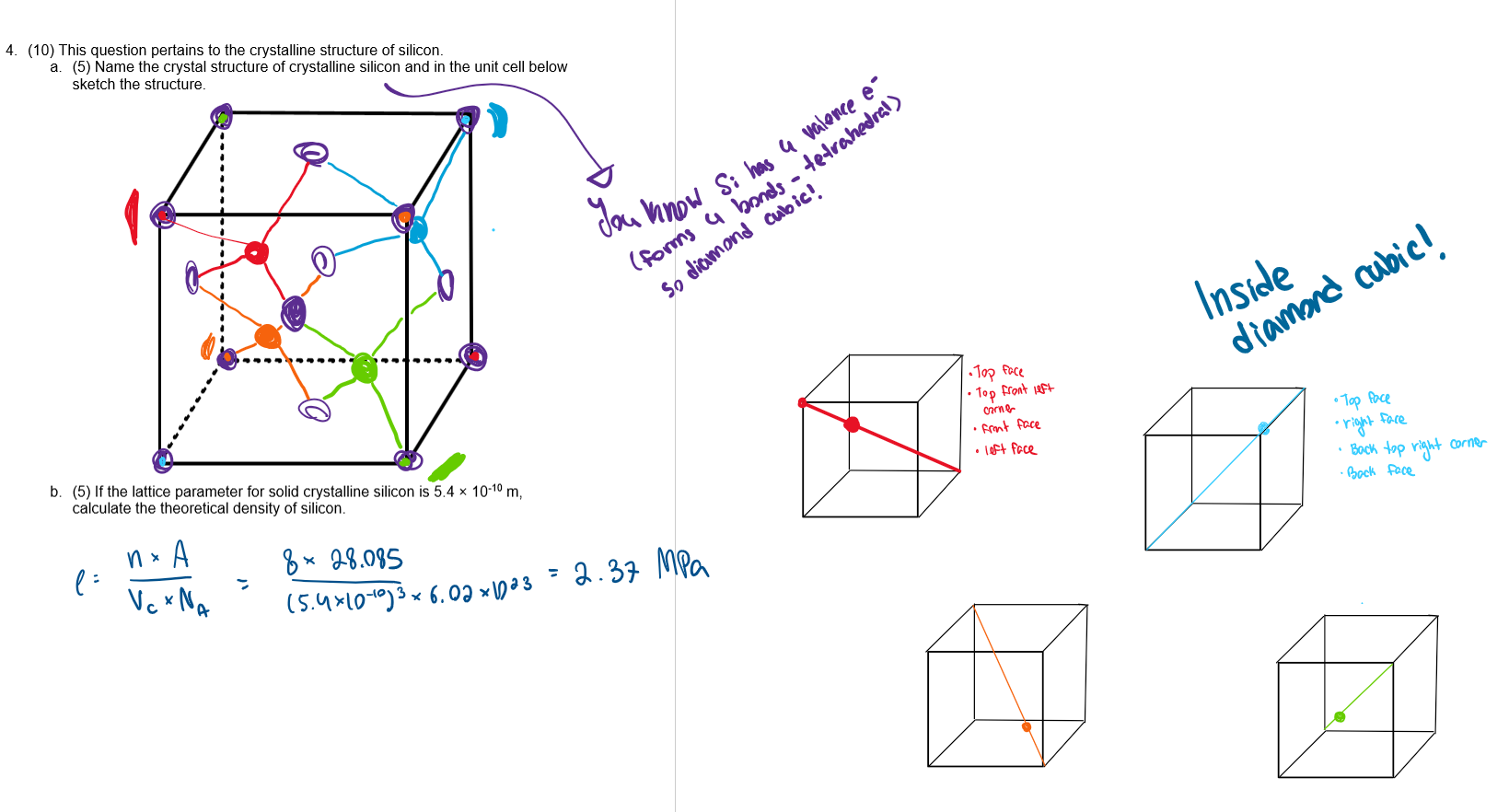
Diamond cubic

a) structure

b) number of atoms (n)

c) coordination number

d) relationship between atomic radius and lattice parameter (a)

a) first draw FCC. Then, add 4 atoms inside, each ¼ of the way along the cube diagonal, so that each atom is bonded tetrahedraly at 109.5 degrees to 4 neighbouring atoms

b) n=8

c) CN=4

d) a=(8/√3)r

nano (ten to the power of…)

-9

micro

-6

milli

-3

mega (M)

6

Giga

9

Tera

12

APF (atomic packing factor)

• fraction of volume occupied by spheres

• (n*volume of one atom)/(volume of unit cube)

• 0.74 for FCC and HCP, can’t be higher than that ever

Plastic deformation mechanism (what’s going on)

• rows of bonds breaking step by step

• step by step movement of linear imperfections

• bonds break only a few at a time due to imperfections slowing deformation

what are the 3pt bend test and tensile test used to determine

E (young’s modulus)

Tempered glass

1. glass heated, then rapidly cooled

2. surfaces cool faster, compressing as they do. centre is still molten

3. when core cools, it is in tension since surfaces are in compression

4. ceramics are stronger in COMPRESSION. The surfaces can resist force, the core balances them out

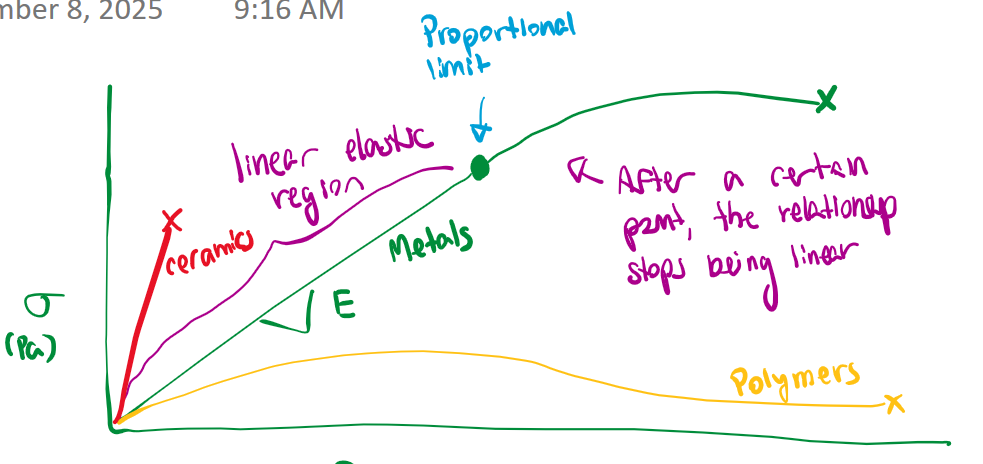
Metal stress strain curve features

1. Starts at 0. First follows linear relationship with E as slope (linear elastic region)

2. 0.2% yield strength: good estimate for the end of elastic deformation/onset of plastic deformation.

• Find strain=0.002

• From there, draw a line parallel to linear elastic region

• stress at the point where this line intersects the curve is yield stress

3. after yield strength: uniform plastic deformation

4. peak of curve: ultimate tensile strength (onset of necking)

5. necking: non-uniform plastic deformation, curve falls until fracture (cross sectional area decreases rapidly)

necking

1. starts at UTS. Ends at fracture

2. Strain hardening of metal does not increase fast enough to keep up with stress increase due to decreased x-sectional area

pico

-12

octahedral interstitial site

When CN=6

imagine cartoon diamond shape

• present in FCC, HCP, rock salt

• Can fit an atom with radius of 0.414 times the radius of the atoms that make up the lattice

Engineering stress (relate to necking)

F/INITIAL area, so as actual area decreases engineering stress decreases (on the graph)

proportional limit

yield strength

Why don’t ceramics plastically deform?

Metals: layers sliding over one another

Ceramics: cations and anions normally in chess-board pattern, but if you slide them they end up adjacent to like charges and repel

MPI

Material Property Index

On a log(E) vs log(density) graph, we want to maximize MPI (High MPI means high E low density)

Young’s modulus: definition and 3 things that CAN change it

Definition: Measure of how stiff an atom’s bonds are when you ELASTICALLY deform them (not plastic deformation!)

To change it:

1. Change the bond type/strength

2. Change atomic spacing

3. Change polymer crystallinity

Does plastic deformation affect atomic spacing/bond length?

No

Stress relaxation

Occurs in polymers, elastomers, composites:

When stress decreases overtime while held at the same pressure, occurs faster at higher temperatures

Lever rule (phase diagrams) - what does it tell us?

Ex. we are looking at 5 wt% C at 1000K, and at that point 2 phases are present: A and B

Using tie lines: we can see what percent composition C A is, and what composition C B is. (ex. maybe A is 10 wt% C and B is 40 wt% C)

Using the lever rule, we can find out the actual weight fraction of each phase (ex. 2/10 of the total mass is made up of the A phase)

Lever rule formula

(Weight of your phase / Total weight) = Composition (wt%, using tie line) of the phase you don’t want minus the overall wt% at the point you’re looking at, all over the composition of the phase you don’t want minus composition of the one you do want

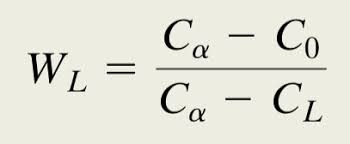
How do you find standard combustion enthalpy of a reaction?

Standard formation enthalpy of PRODUCTS minus REACTANTS (P minus R)

Conductor band structure

Conduction band on top, valence band on the bottom

Insulator band structure

Conduction band on top, valence band on bottom, large band gap (for electrons to be conducted an electron would need enough energy to be promoted across the huge band gap)

Note: electrical conductivity CAN occur in an insulator if an electron gets enough energy to cross the band gap. In the conduction band, it is free to move

Intrinsic semiconductors and formula for their conductivity

Intrinsic:

• one hole created per promoted electron

• all charge carriers come from the semiconductor itself

• for attached formula: n=p for instrinsic, and q/e (the elementary charge) is always equal, so you can write it as sigma=nq(mn+mp)

  • sigma: conductivity

  • n: number of holes=number of electrons

  • q: fundamental charge

  • mn/mp: electron and hole mobilities

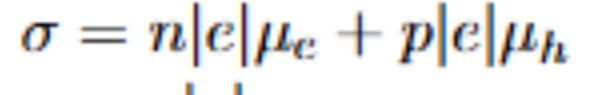
Extrinsic semiconductors

Added impurities (dopants) to control conductivity

2 ways to dope:

• n-type (adding electrons)

  • add anything with MORE valence electrons than your semiconductor (RIGHT on periodic table)

• p-type (adding holes)

  • add anything with FEWER valence electrons (left on periodic table)

n-type semiconductor band structure

valence band at the bottom, then smaller band gap, then conduction band.

small line BELOW conduction band (right at the top of the band gap) is the DONOR level

• adding a dopant with extra electrons: the new electron is weakly bonded, easily promoted, very little energy to promote

• “donor energy level”: contains the added electrons that are easy to promote

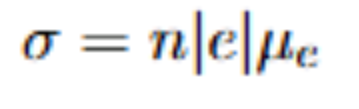
What type of defect are the dopant atoms in extrinsic semiconductors

point defects

p-type semiconductors band structure

Same as n-type, except small “acceptor level” at the bottom of the band gap, just above the valence band

• Doping elements with fewer valence electrons adds a hole for each dopand atom

• electrons can be promoted to holes with much less energy. The holes create the acceptor energy level

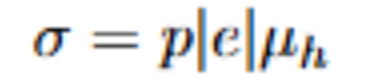
Point defects (and 3 examples)

If the defect concerns one specific atom’s position, composition, or site occupancy, it’s a point defect.

ex:

• vacancy (missing atom)

• interstitial occupancy (extra atom squeezed in)

• substitutional impurity (like replacing an Si atom with a dopant atom

Linear imperfections

Defects with length, but very small width

• plastic deformation

• dislocation movement

• edge dislocation

Interfacial defects

2-D: boundaries between two regions with different phases, orientations, or structures (any FLAT region separating two parts of a material)

ex.

• grain boundaries

• phase boundaries

Volume defects

3-D:

ex.

• voids (holes)

• cracks

• pores

• inclusions (like oxide particles in steel)

• cluster of vacancies

anything that has a width, height, and length of more than one atom, that would be visible under a regular microscope

How do polymers continue load bearing after necking?

Molecules become oriented along the loading axis

• oriented polymers are MUCH stronger

• “deformation by drawing” strengthening mechanism: drawing out polymers to orient them

For polymers, what does molecular weight describe

How long they are

2 ways to describe average molecular weight (length) for polymers

1. number average

• sum of all the weights over the number of molecules (easy)

2. weight average

• Sum of weighted fractions of each “bin” over the total

Weight average: how do you calculate it?

ex. imagine we have a bunch of polymers of different lengths, grouped by their lengths into different “types”

In the attached formula, Mw is weight average, Ni is the number of chains of type i, and Mi is the mass of the chains in that group.

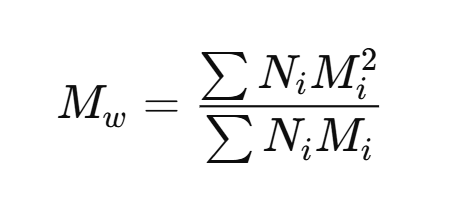
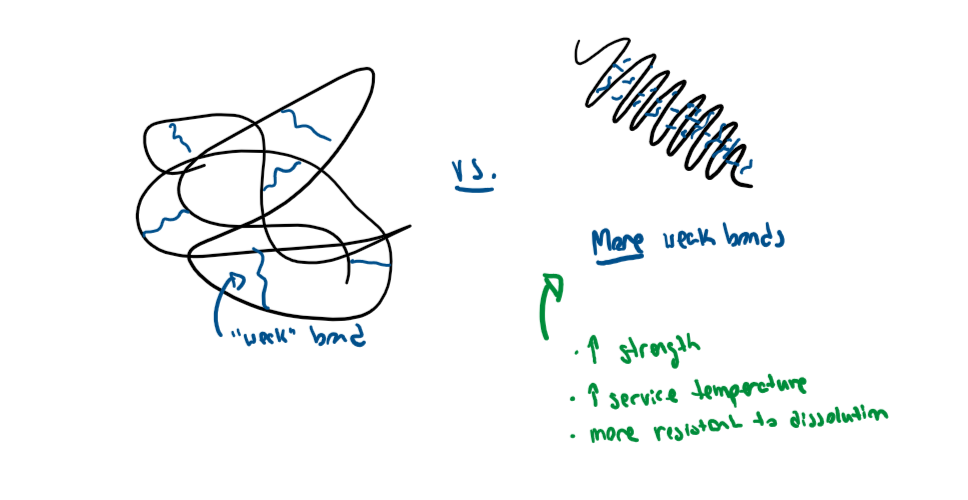
What is the max percent crystalline that a polymer can be? the max percent amorphous?

Can’t be more than 80% crystalline

Can be 100% amorphous

Crystalline vs amorphous polymers strength

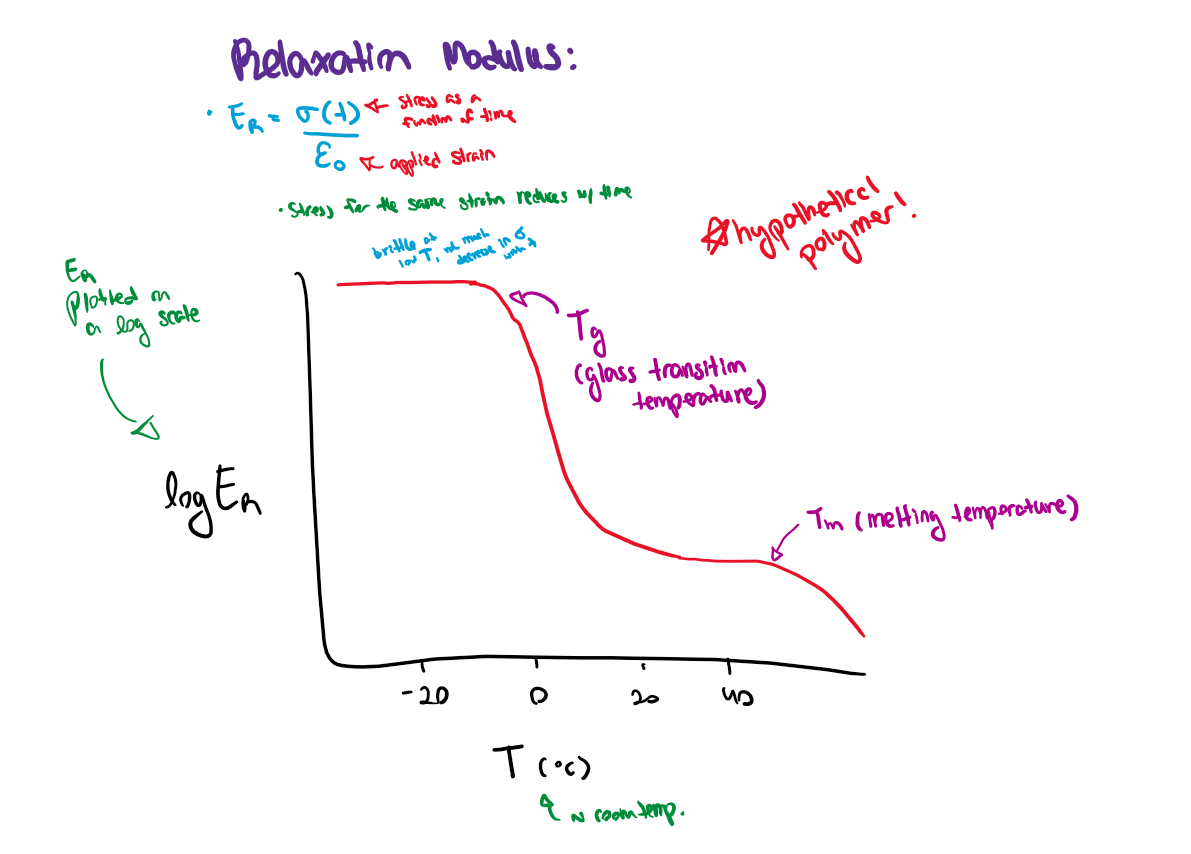
Relaxation modulus

E=(stress as a function of time, sigma of t) / strain

Stress for the same strain reduces with time

Relaxation modulus vs time features

As temperature increases:

1. Tg - thermal energy overcomes weak secondary interactions in amorphous regions (glass transition temp)

2. Tm - thermal energy overcomes weak secondary interactions in crystalline regions (melting temp)

Requirements for optical transparency

1. no internal scattering events

2. HIGH band gap (why fully amorphous metal’s aren’t transparent - no band gap)

What is an electron volt

1 eV = 1.602 × 10^-19 J = q (the fundamental charge)

What is the faraday constant

The charge of one mole of electrons:

equal to q, or 1 eV (the charge of one electron) times Avagadro’s number (the number of electrons in a mole, or the number of anything in a mole)

what quantum number describes size of orbit? what can it be?

n

n can be 1,2,3,4, etc

what quantum number describes shape? what can it be?

l (always l=n-1)

l=0: s shaped (sphere)

l=1: p shaped (dumbell)

l=2: d

l=3: f

(only s and p orbitals are involved in bonding)

what quantum number controls orientation

m_l (must be between -l and l)

ex. for p-subshell, (l=1) this one can be -1, 0, or 1. There are three possible ways to orient a p orbital. For s (a sphere) there is only one

what quantum number controls spin

m_s (can only be -1/2 or 1/2)

Slightly different energy level for 2 electrons in the same orbital, so they are distinguished based on their spin. In any given orbital, there can be at most 2 electrons

Cr and Cu electron configurations

Cr: [Ar]3d54s1

Cu: [Ar]3d104s1

Non-directional bonding (def and examples)

All electrons are equally attracted to all neighbours (ex. ionic, metalllic)

Directional bonds

Covalent - only occur between specific atoms

Explain band theory

electron configurations - very distinct energy levels, describing just one atom

But what if we have a solid with a lot of atoms very close to one another?

• atoms can’t share energy levels, so as they get very close, their energy levels slightly spread out so for each energy level that you would have in an isolated atom there are 2 when 2 atoms are close by, 3 for 3 atoms, up until you get a huge band that is basically a continuous spectrum

Entropy definition

q(rev)/T (heat transferred reversibly over temperature in K)

delta U (change in internal energy)

(energy change required to make more products) - (energy required to make more reactants)

State function vs path function, one example of each

State - doesn’t matter how we got there (temp, U)

Path - work

Isolated vs closed system

Isolated: No heat exchanged with surroundings, delta U is 0

Closed: heat can pass (no matter exchanged for both)

delta U = q + w

(change in internal energy is equal to heat transferring IN to the system plus work done ON the system)

When is Δ U = q+w

closed system

Positive Δ H?

Endothermic

Equilibrium definition

forward and reverse reactions proceed at the same rate

K vs Q equilibrium

Q - reaction quotient

K - what Q becomes AT EQUILIBRIUM (equilibrium constant)

If the reaction favours the products (forward reaction is spontaneous) what do we know about ΔG plimsol and K

ΔG plimsol is less than zero

K is greater than 1

(vice versa for favouring reactants)

Standard reduction potential: who is more likely to get reduced?

The one with the more positive standard reduction potential

Nernst equation what does it tell us

• first equation under electrochem in the data booklet (with the two Es)

• lets us find cell potential at concentrations and temperatures that aren’t equilibrium (E plimsol is the equilibrium one)

Range of radius ratios for different interstitial sites and their CN

less than 0.414: tetrahedral (CN 4)

0.414-0.732: octahedral (CN 6)

more than 0.732: cubic (CN 8)

4 polymer strengthening mechanisms

1. strain hardening - drawing them out along the loading axis, creating friction that resists sliding

2. cross linking - creating permanent ionic or covalent bonds between chains, resisting sliding and greatly increasing strength (and young’s modulus!)

3. increasing crystallinity - increased stiffness, density, strength

4. increasing chain length - more entanglement

Reaction quotient

Q

a of each species is its activity

• concentration

OR

• Partial pressure (if it’s a gas)

Usually okay to leave it in terms of partial pressure if not given!

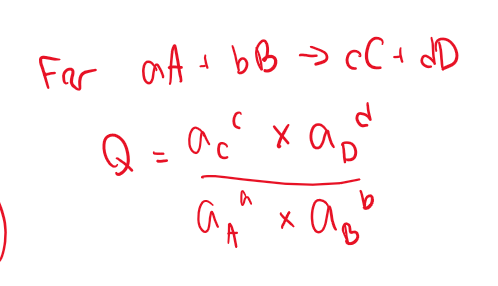
How do you do weight average like for real

multiply how many are in that group by the weight of each thing in that group squared, over the sum of ALL the groups number times weight (a bit confusing but ill attach an example)

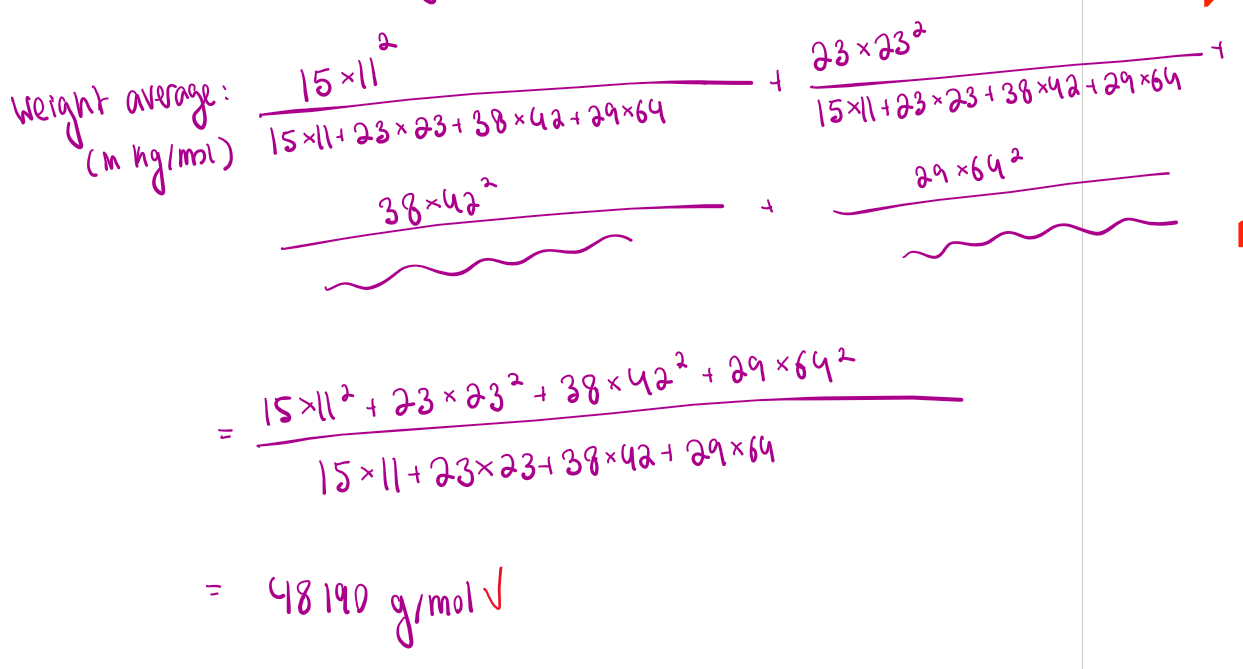
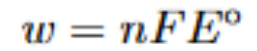
What is this formula

should be w=-nFE

work done by the cell is equal to (negative) number of electrons transfered, times faraday constant, times E of the cell (which is the cell potential, equal to E of the one being reduced minus E of the one being oxidized). This is the same as the gibbs free energy of the cell, delta G equals -nFE

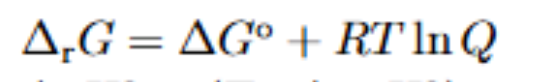
What is this at equilibrium

Reaction gibbs energy is zero at equilibrium and Q is K, so it becomes

Standard G = -RTlnK

What is solid solution strengthening and does it affect Young’s modulus

dissolving atoms of another element into the crystal lattice of a metal, yes it can increase it

what is cold working and can it impact young’s modulus

shaping (rolling, bending, etc) a metal at around room temp to cause work hardening, increasing strength and stiffness but reducing ductility (can affect young’s modulus but not a lot and probably say no for this exam)

How does plastically deforming a metal change its mechanical properties

• Plastically deforming it greatly increases the number of dislocations

• increased dislocation density makes it harder for dislocations to move

• plastic deformation IS the movement of dislocations, so it makes plastic deformation harder

• this is what STRAIN HARDENING is

• increases yield strength and hardness, NOT stiffness (no change to E)

Describe how you would answer this question

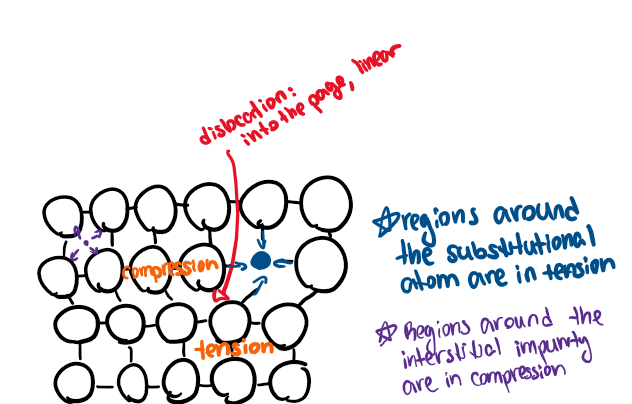
what do you keep forgetting for

a) APF

and

b) entropy

a) you have to multiply by the number of spheres

b) it is given in J, you need to convert

What type of polymers can melt? What type decompose and don’t melt?

Thermoplastics melt

• NOT cross linked/network

• long, linear chains with weak forces between them

Thermosets don’t met, they char/burn

• chain linked/network polymers

• strong, permanent

describe how to draw diamond cubic and what’s going on

1. FCC

2. the cube has 4 diagonals. following these 4 diagonals, pick 4 vertices (one on each diagonal) so that 2 are on top 2 on the bottom, and 2 are at the front 2 at the back

3. ¼ of the way along the diagonals, there is an atom. It is bonded to 4 other atoms: the one in the corner it is closest to, and the 3 atoms on the 3 faces that that corner is touching

Something doesn’t conduct electricity. Relate that to band theory

insulators have a large band gap