1.5. Vorticity equations

General integral form of conservation of mass (formula) (Navier Stokes equation)

formula

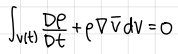
General integral form of conservation of momentum (formula) (Navier Stokes equation)

formula

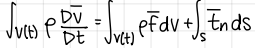
General integral form of conservation of total energy (formula) (Navier Stokes equation)

formula

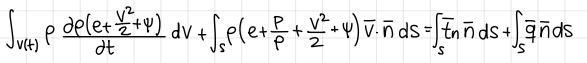
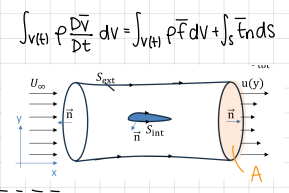
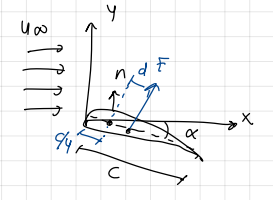
developing of aerodynamic force of an airfoil

developing

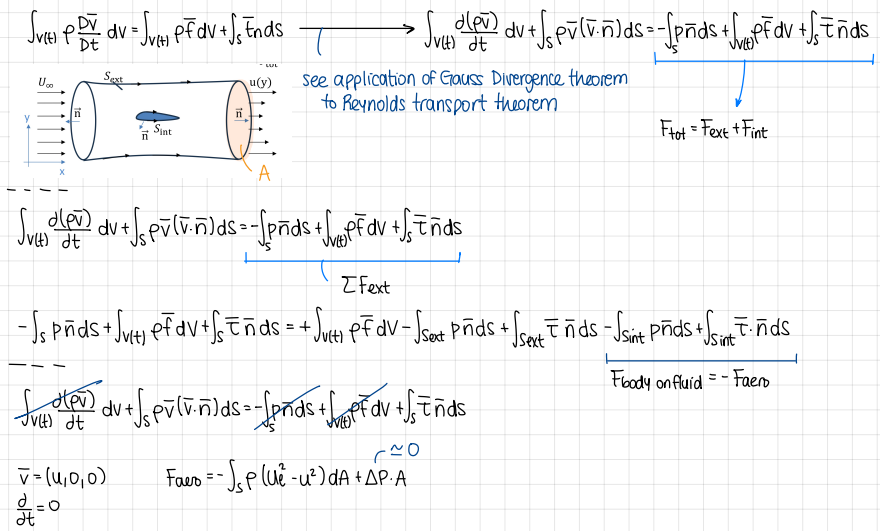
origin of aerodynamic forces (formula)

formula

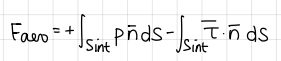
differential form of conservation of mass (formula) (Navier Stokes equation)

formula

1eq, 4ukn

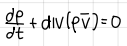
differential form of conservation of momentum (formula) (Navier Stokes equation)

formula

3eqs, 7ukn

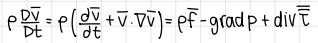
differential form of conservation of energy (formula) (Navier Stokes equation)

formula

1eq, 2ukn

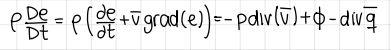
Constitutive equations (4 formulas) (Navier Stokes equation)

formulas

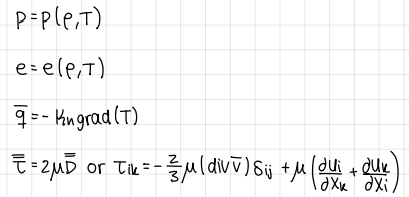
Initial conditions (3 IC) (Navier Stokes equation)

IC

Boundary conditions (2 BC) (Navier Stokes equation)

BC

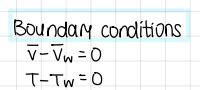
differential form of conservation of mass (formula) (INCOMPRESSIBLE Navier Stokes equation)

formula

1eq, ukn

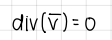
differential form of conservation of momentum (formula) (INCOMPRESSIBLE Navier Stokes equation)

formula

3eqs, ukn

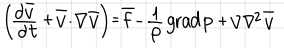
differential form of conservation of energy (formula) (INCOMPRESSIBLE Navier Stokes equation)

formula

in general only needed for non-adiabatic flows

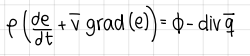
Constitutive equations (4 formulas) (INCOMPRESSIBLE Navier Stokes equation)

formulas

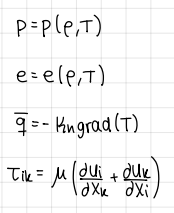
Initial conditions (3 IC) (INCOMPRESSIBLE Navier Stokes equation)

IC

Boundary conditions (2 BC) (INCOMPRESSIBLE Navier Stokes equation)

BC

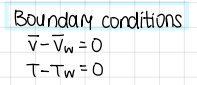
Consequences of incompressible flow model

• Density is constant everywhere

• Compressibility is zero → infinite speed of sound

• Any change of flow is felt instantly in every point of the field (not possible to model sound transmission)

• Energy equation is decoupled from momentum and mass conservation (often not necessary)

• M=0 → strictly valid only for low speed flows (but physical mechanisms are valid up to higher Mach numbers (with corrections))

Development and equation of vorticity and viscous term

development and equation

what is ψ?

body force (conservative)

development and equation of Bernoulli’s theorem.

development and equation

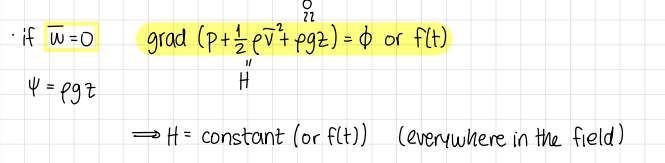
what is H in Bernoulli’s theorem?

constant everywhere in the field

what does it mean when a field is conservative?

the work done to move between two points doesn't depend on the path taken

The generalized Bernoulli’s theorem is also called…

weak form of Bernoulli’s theorem

generalized version (weak form) of Bernoulli’s theorem: development

development

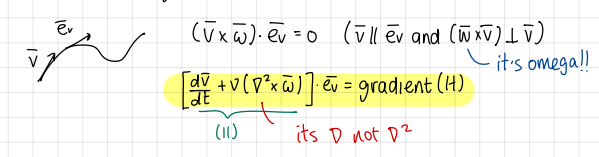
Streamline definition

line tangent to the velocity of the flow at every point

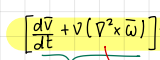
if this term of the generalized Bernoulli’s theorem is zero, …

H is constant along streamlines

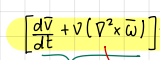
this term of the generalized Bernoulli’s theorem is constant if…

• assume steady flow (d/dt=0)

• omega=0

• upsilon«1

• omega is constant

Flow types with constant or zero vorticity

• Solid body rotation

• Uniform flow

• Ideal vortex

• Rankine vortex

Solid body rotation: drawing and equations

drawing and equations

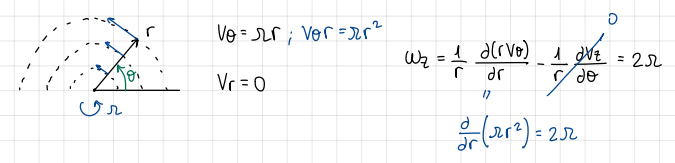
Uniform flow: drawing and equations

drawing and equations

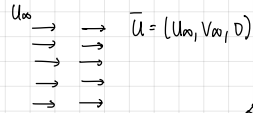
Ideal vortex: drawing and equations

drawing and equations

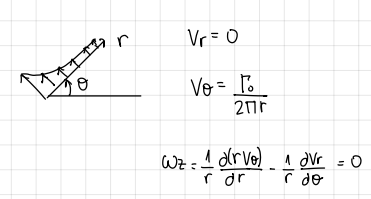
Rankine vortex: drawing

drawing

In order to have velocity potentials, the flow must be…

invsicid/irrotational

Development of velocity potential (inviscid/irrotational flows)

development

write the 3 equations + condition of the potential flow model

equations

General results for incompressible flow model

• Aerodynamic force

• Kutta-Jukovsky theorem

• Circulation

• D’Alembert paradox

• Amount of solutions

• Kutta condition

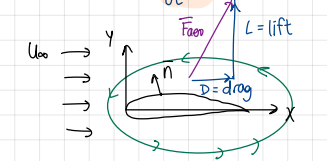
Aerodynamic force formula (general results for incompressible flow model)

formula

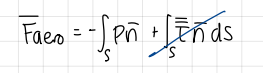
Kutta-Jukovsky theorem formula (general results for incompressible flow model)

formula

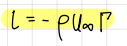
Circulation formula (general results for incompressible flow model)

formula

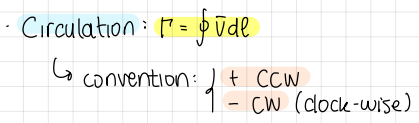
D’Alembert paradox formula (general results for incompressible flow model)

formula

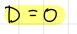
Amount of solutions (general results for incompressible flow model)

infinite solutions for a given geometry (one for each circulation (Gamma) value)

Kutta condition (general results for incompressible flow model)

velocity at the trailing edge is zero (it’s a stagnation point)

Computational methods to solve potential flow equations

• Fundamental solution of Laplace equations (cylinder with and without circulation)

• Conformal mapping (map cylinder into airfoil-shape body)

• Thin airfoil theory (neglect thickness distribution)

• Panel methods (discretized solution on realistic shapes)

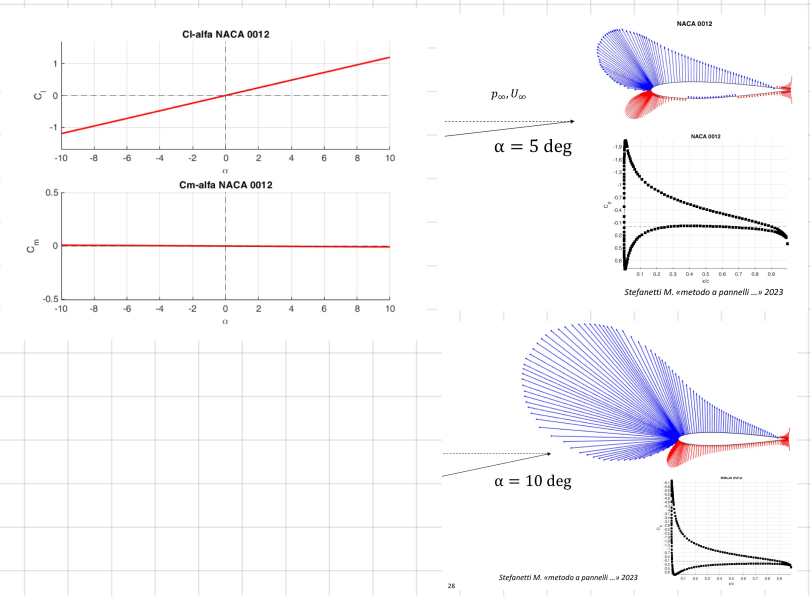
Main results for thin airfoils (formulas)

formulas

quite realistic results for streamlined bodies (airfoils) of finite thickness

Main results for thin airfoils: pressure distributions (graphs)

graphs

Formula of pressure coefficent Cp

formula

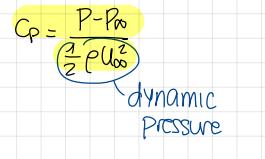
What happens to the pressure coefficent at a stagnation point?

Cp=1

(U=0)

Issues and limits of potential flow models

solution of potential flow model for streamlined bodies turn out to provide a good approximation of real flows, and reasonably good estimates for Lift and Aerodynamic moments at limited angles of attack, but :

• what is the physical rationale for using the slip-velocity boundary condition?

• can the flow really be considered irrotational?

• what is the physical origin of Circulation (Lift)?

• how can we compute maximum CL values (stall)?

• what is the physical origin of drag?

• how can we model/estimate drag?

• what about less streamlined body shapes?

Aerodynamic loads on a solid body arise from…

We need to solve equations to…

the integral of normal and tangential stresses acting on the body surface

determine the distribution of normal and tangential stresses

Viscous effects are strictly related to…

the vorticity field (kinematic effects) → if vorticity is zero the flow is inviscid

If a flow is inviscid, we can…

derive a linear system of equations that can describe the slipping motion of a fluid around a solid body

For a 2D body lift (related to normal stresses) can be calculated from…

Drag is always equal to…

the circulation of the velocity (Kutta-Jukowsky theorem)

zero for an inviscid 2D body

We need to evaluate origin and dynamic of vorticity to…

• to give a physical interpretation of the potential flow model

• to evaluate viscous phenomena (stall , separation, drag...)