Statistics in Psychology: Belief Bias, Simpson’s Paradox, and Data Analysis Tools, Elementary Statistics: Scales, Central Tendency, and Variability for Data Analysis, Elementary Statistics: Normal Distribution, Z-Scores, and Probability, Elementary S…

Why is statistics important in psychology?

Statistics help us trust our data and analyze it critically, addressing biases in our instincts.

What is belief bias?

Belief bias is the tendency to accept ideas or arguments that align with one's values, beliefs, and prior knowledge.

What is a common issue with common sense in psychology?

There is no common standard for common sense, leading to varied interpretations and beliefs.

What is Simpson's Paradox?

Simpson's Paradox is a phenomenon where a trend appears in several groups of data but disappears or reverses when the groups are combined.

What is the take-home message regarding biases and statistics?

We can't trust our instincts due to biases, so we need to think critically about statistical analyses.

What are the two main types of statistics used in psychology?

Descriptive statistics, which summarize data, and inferential statistics, which extend conclusions beyond the immediate data.

What do descriptive statistics provide?

Descriptive statistics provide simple summaries about the sample and the measures, such as mean and standard deviation.

What do inferential statistics do?

Inferential statistics infer properties of a population using statistical analysis of a sample.

What are some examples of inferential statistical methods?

Regression analysis and ANOVA (Analysis of Variance) are examples of inferential statistical methods.

Name some user-friendly statistical applications.

SPSS, Jamovi, JASP, and business tools like Excel, Power BI, and Tableau are user-friendly statistical applications.

What is required to use some statistical applications like R or Python?

Writing code is required to use statistical applications like R and Python.

What was the study by Evans, Barston, and Pollard (1983) about?

The study explored the conflict between logic and belief in syllogistic reasoning.

What is the significance of thinking critically about statistics?

Thinking critically about statistics ensures that we do not blindly trust any statistical analysis and helps us understand our data better.

Nominal Scale

A scale of measurement where categories are mutually exclusive, such as sex (female vs. male) or political party (Republican vs. Democrat).

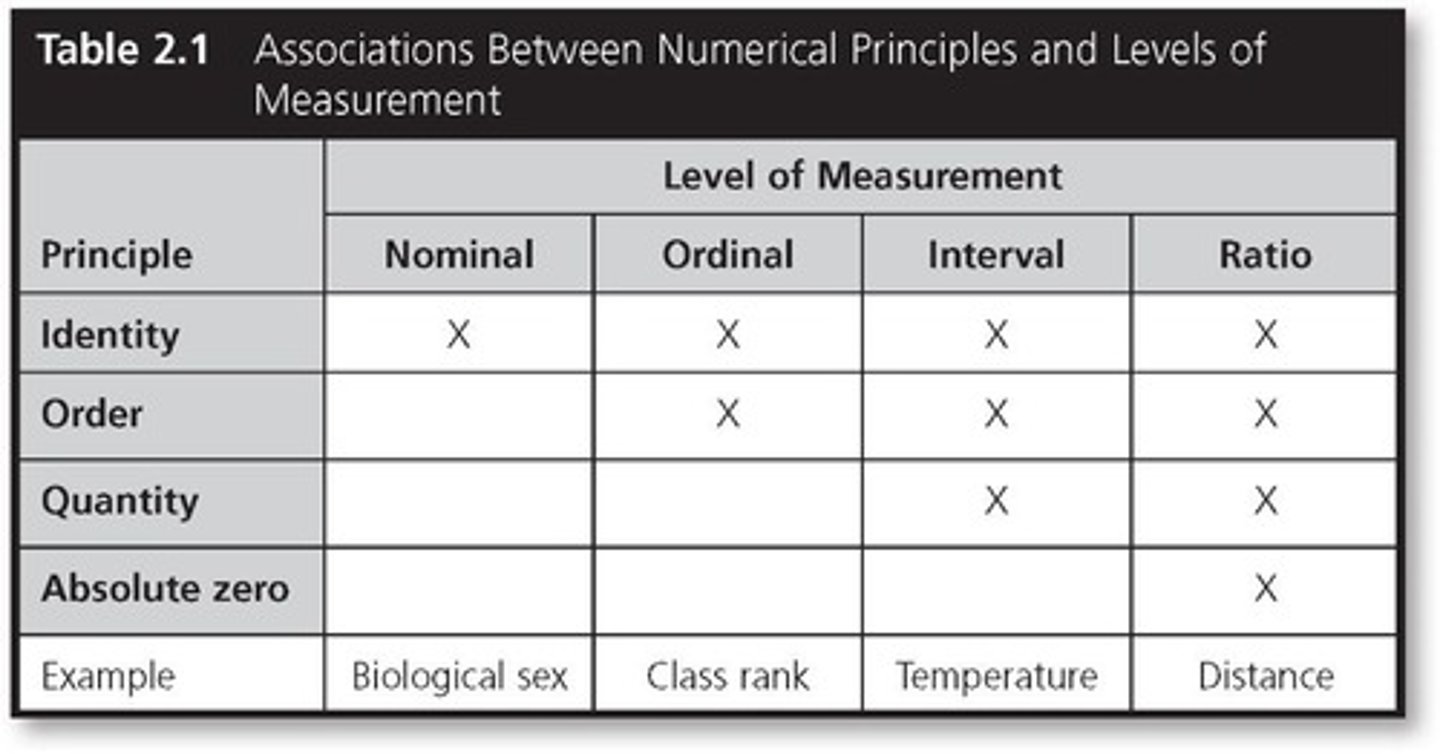
Ordinal Scale

A scale of measurement that ranks items in order, starting with 1, but does not provide information about the distance between ranks.

Interval Scale

A scale of measurement where the distance between any two adjacent points is the same, but zero does not indicate the absence of the quantity.

Ratio Scale

A scale of measurement that has equal intervals and a true zero, allowing for meaningful ratios, such as weight or time.

Categories

Groups into which data can be classified, such as sex, political party, or documentation status.

Levels

The values that a particular categorical variable can take, such as male or female for the variable sex.

Mutually Exclusive Categories

Categories that do not overlap, where an item belongs to one category only.

Practical Distinction

A workable classification where categories are not strictly mutually exclusive, such as university employee type.

Unclear Categories

Categories that are problematic due to overlap, such as types of musicians.

Top-ten List

An example of an ordinal scale where the lowest rank is always the total number of items, such as 10.

Likert Scale

An interval scale used in psychology to measure attitudes, with responses ranging from strongly disagree to strongly agree.

Temperature

An example of an interval scale where the difference between temperatures is consistent, but zero is arbitrary.

True Zero

A mathematically relevant value of zero that indicates the absence of the quantity being measured.

Equal Intervals

A characteristic of ratio scales where the difference between points is always the same.

Meaningful Ratios

A feature of ratio scales where ratios such as 'twice as much' are valid.

Angle in Degrees

An example of a ratio scale where 90 degrees is twice as wide as 45 degrees.

Time in Milliseconds

An example of a ratio scale where 100 ms is twice as long as 50 ms.

Weight

An example of a ratio scale where 300 lbs. is twice as heavy as 150 lbs.

Data Analysis Methods

The choice of methods depends on the type of scale being used for measurement.

Race Groups Analysis

An example question regarding the analysis method to examine if race groups affect hiring decisions.

Caucasian

A racial classification typically used to describe people of European descent.

Hispanic

A term used to refer to people of Spanish-speaking origin or descent.

Hired

Individuals who have been employed or selected for a job.

Not Hired

Individuals who have not been employed or selected for a job.

ANOVA

Analysis of Variance, a statistical method used to compare means among three or more groups.

Chi-square test of independence/association

A statistical test to determine if there is a significant association between two categorical variables.

Operationalization

Transforming a meaningful yet somewhat ambiguous concept into a precise measurement.

Continuous variables

Variables characterized by the logical possibility of having another value between any two values you can think of.

Discrete variables

Variables that do not have values in between certain points.

Dependent variable (DV)

The outcome variable that is measured in an experiment, which is affected by the independent variable.

Independent variable (IV)

The variable that is manipulated or controlled in an experiment to test its effects on the dependent variable.

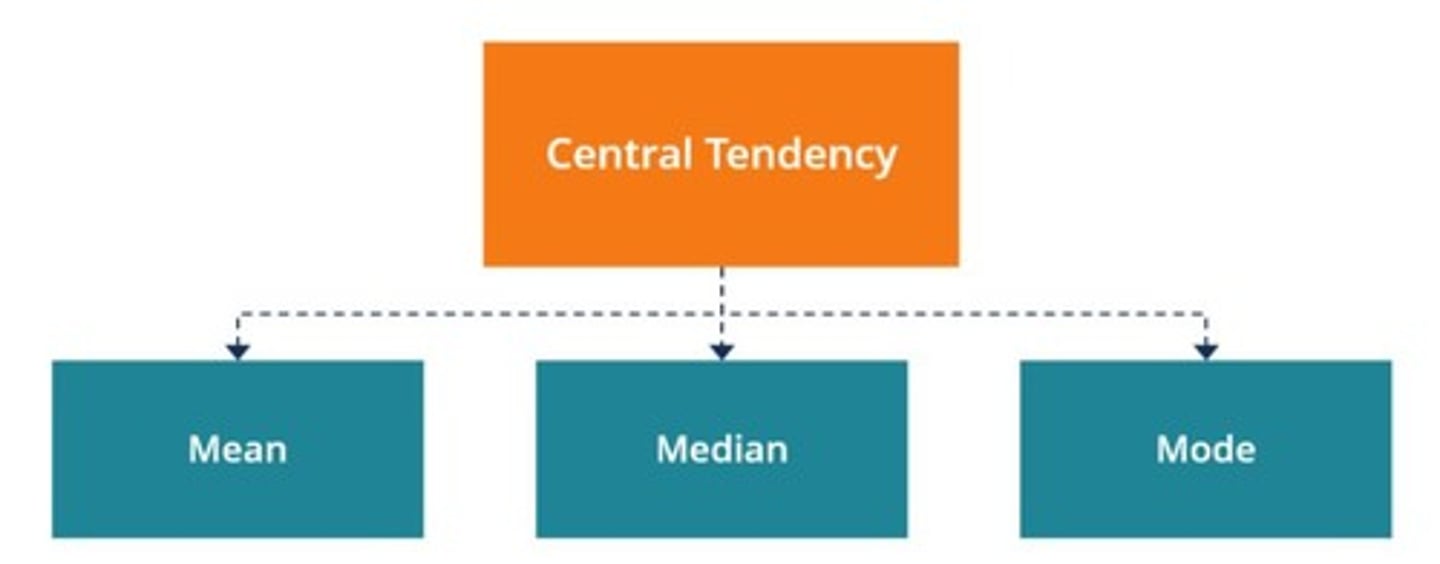
Central Tendency

A descriptive summary of a dataset through a single numerical value that reflects the 'center' of the data distribution.

Descriptive Statistics

Statistics used to describe the basic features of the data, providing simple summaries about the sample and the measures.

Inferential Statistics

Statistics that try to reach conclusions that extend beyond the immediate data alone, inferring properties of a population using a statistical analysis of the sample.

Mean

The most familiar measure of central tendency, computed by summing all values and dividing by the number of values.

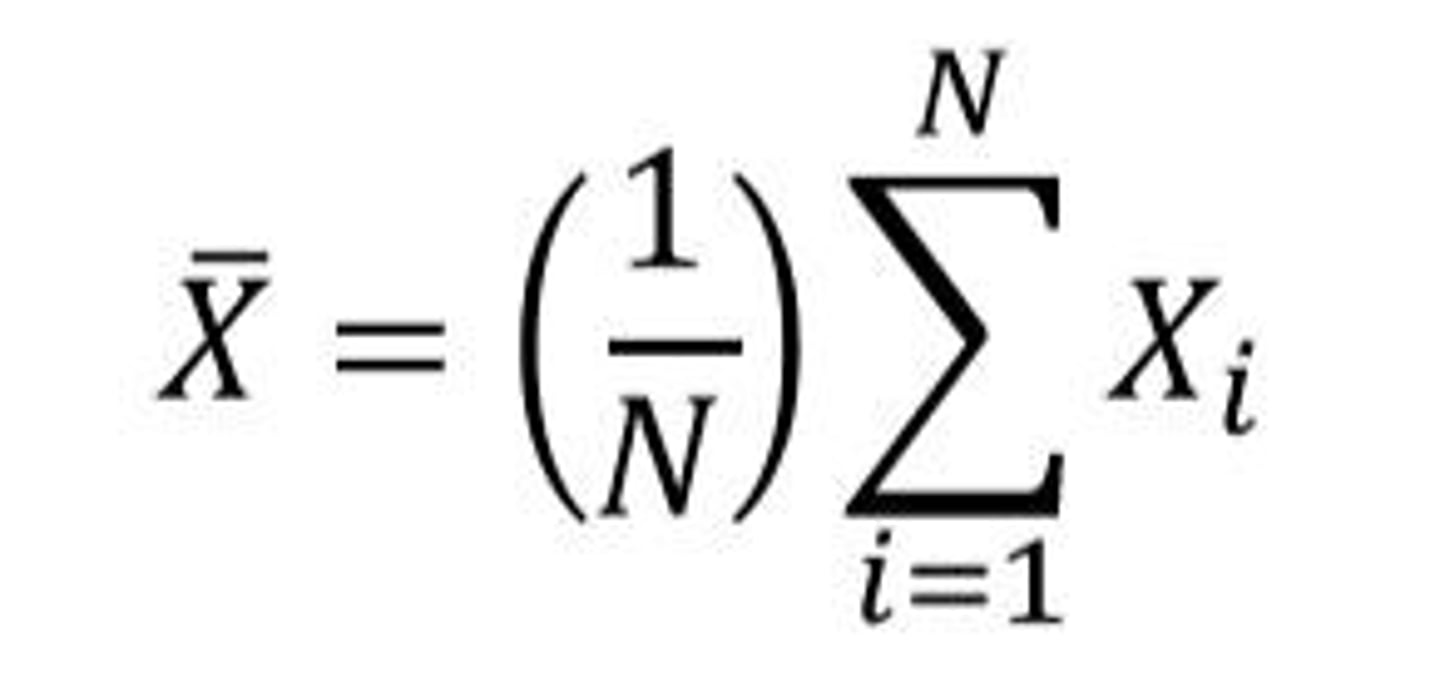
Statistical Notation

A system of symbols used to represent mathematical concepts and operations in statistics.

Skew

A measure of the asymmetry of the probability distribution of a real-valued random variable.

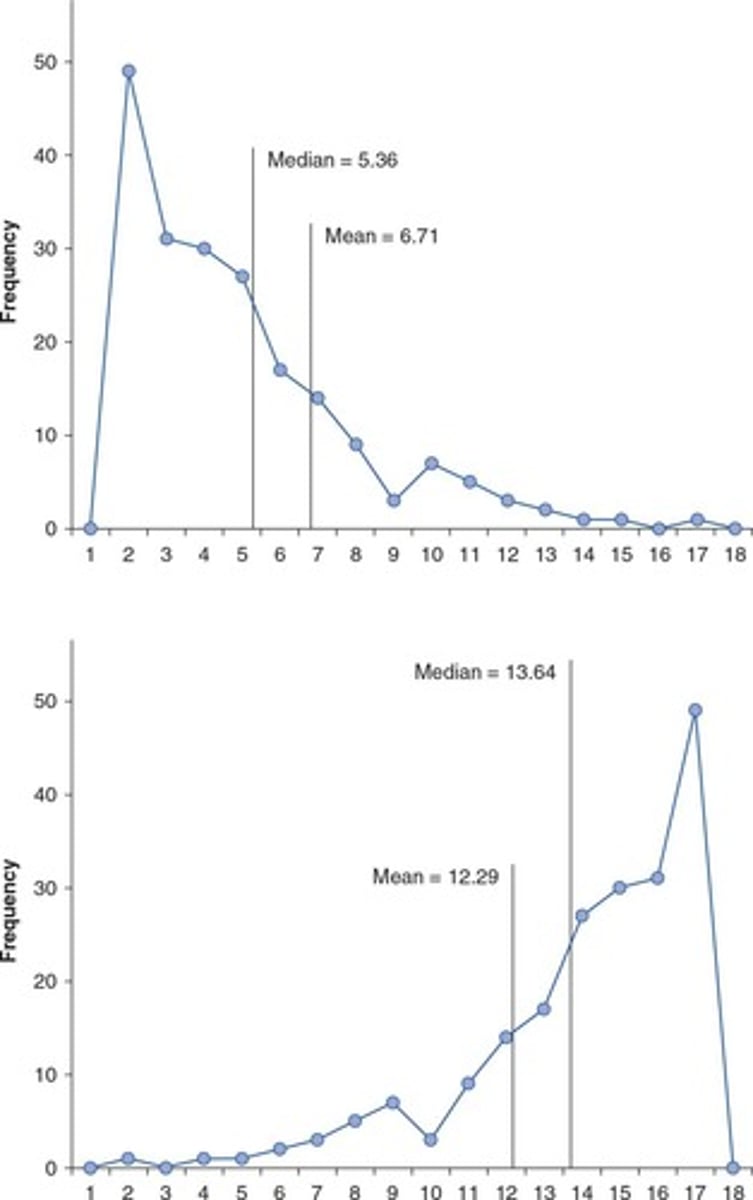
Kurtosis

A measure of the 'tailedness' of the probability distribution of a real-valued random variable.

Variability

A measure of how spread out the values in a data set are.

Sample Mean Formula

The formula for computing the sample mean is (X1 + X2 + X3 + X4 + X5) / n, where n is the sample size.

Order of Operations

Please Excuse My Dear Aunt Sally: Parentheses, Exponents, Multiplication, Division, Addition, Subtraction

Median

The middle value in a set of scores, where half of the scores are larger and half are smaller.

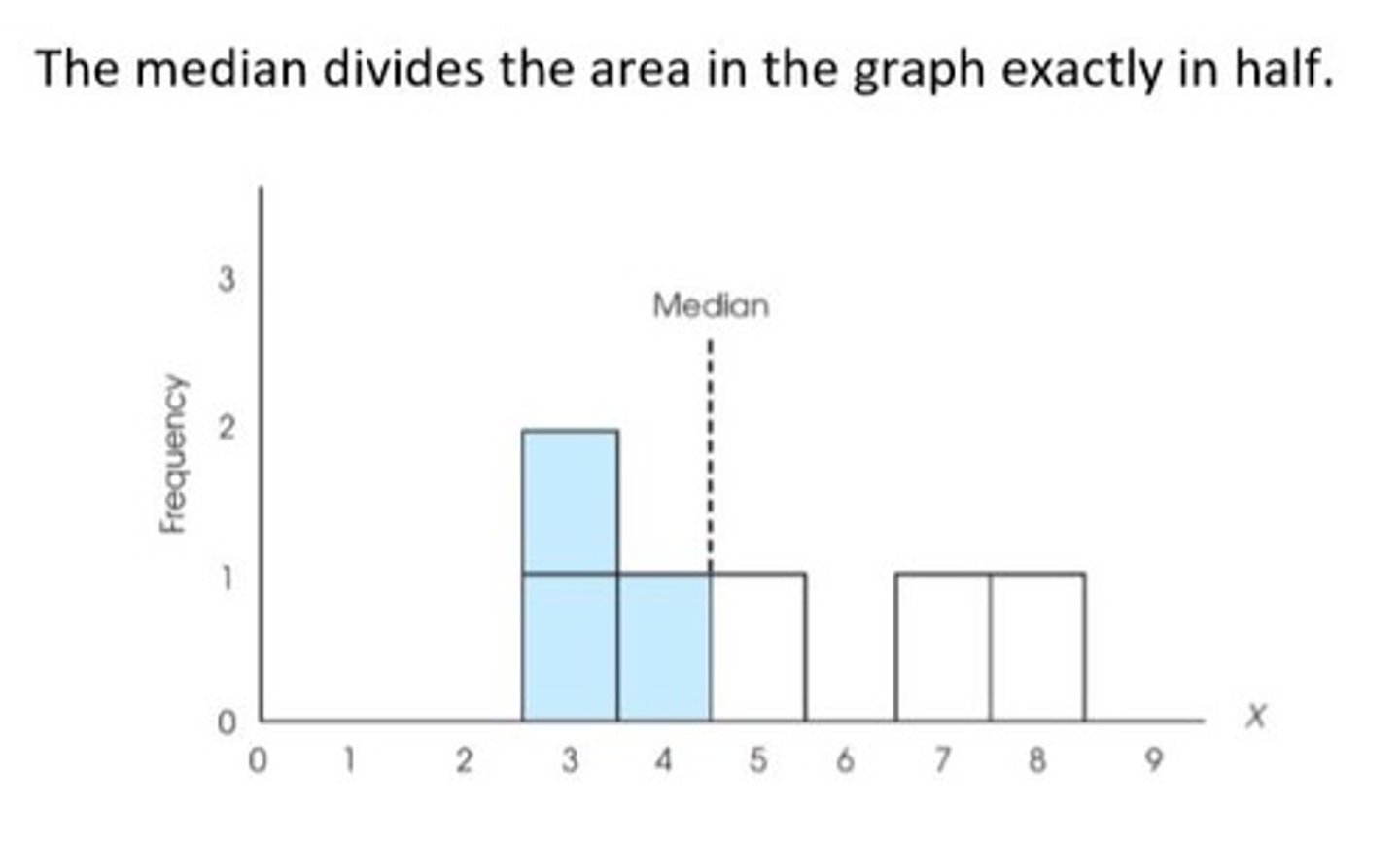
How To Find the Median

1. List values in order (either highest to lowest or lowest to highest). 2. Find the 'middle-most' score.

Median (for Even Number)

If the total sample number is even, average the middle two scores.

Comparing the Mean to the Median

The median is the 'middle value' while the mean is the 'center of gravity' of the data set.

Sensitivity of the Mean

The mean is very sensitive to extreme scores.

Mode

The value that occurs most frequently in the data set.

When to Use Mode

Typically used with nominal (categorical) data.

Bimodal Data Set

A data set that has more than one mode.

Scales and Central Tendency - Nominal

Cannot use either mean or median; best to use mode.

Scales and Central Tendency - Ordinal

Can use median if you use the order information; mean is not appropriate.

Scales and Central Tendency - Interval

Can use mean and median; mean is very sensitive to extreme, outlying values.

Scales and Central Tendency - Ratio

Can use mean and median; mean is very sensitive to extreme, outlying values.

Example of Mean Calculation

Mean: $58,333; Median: $60,000.

Example of Extreme Scores

Mean: $25,043,750; Median: $62,500.

Real Life Example - MLB Salaries

Mean salary of MLB players in 2016 was more than $4 million, median was $1.2 million.

Finding the Mean

Sum all values and divide by the count of values.

Finding the Median with Example

For amounts $11.75, $12.75, $13.00, $10.75, $11.50, $10.50, $10.75, the median is $11.50.

Finding the Median with Even Sample

For scores 20, 21, the median is (20+21)/2 = 20.5.

Formula for Sample Mean

If the sample size is 5, then the mean is computed as (X1+X2+X3+X4+X5)/5.

Median for Even Number

If the total sample number is even, average the middle two scores.

Comparing Mean to Median

The median is the 'middle value', while the mean is sensitive to extreme scores and represents the 'center of gravity' of the data set.

Skew and Kurtosis

Shapes of distributions that describe the asymmetry and peakedness of the data distribution.

Measures of Variability

Describes the spread or dispersion of data.

Practice Mean Calculation

To find the mean of scores 10, 35, 40, 60, 55, 25, 50, sum them and divide by 7 to get approximately 39.29.

Practice Median Calculation

To find the median of amounts $11.75, $12.75, $13.00, $10.75, $11.50, $10.50, $10.75, list them in order and find the middle value.

ΣX

The sum of all X values in a dataset.

ΣY

The sum of all Y values in a dataset.

Data Example

Fall, 2018 A&M Football Scores used for practice calculations.

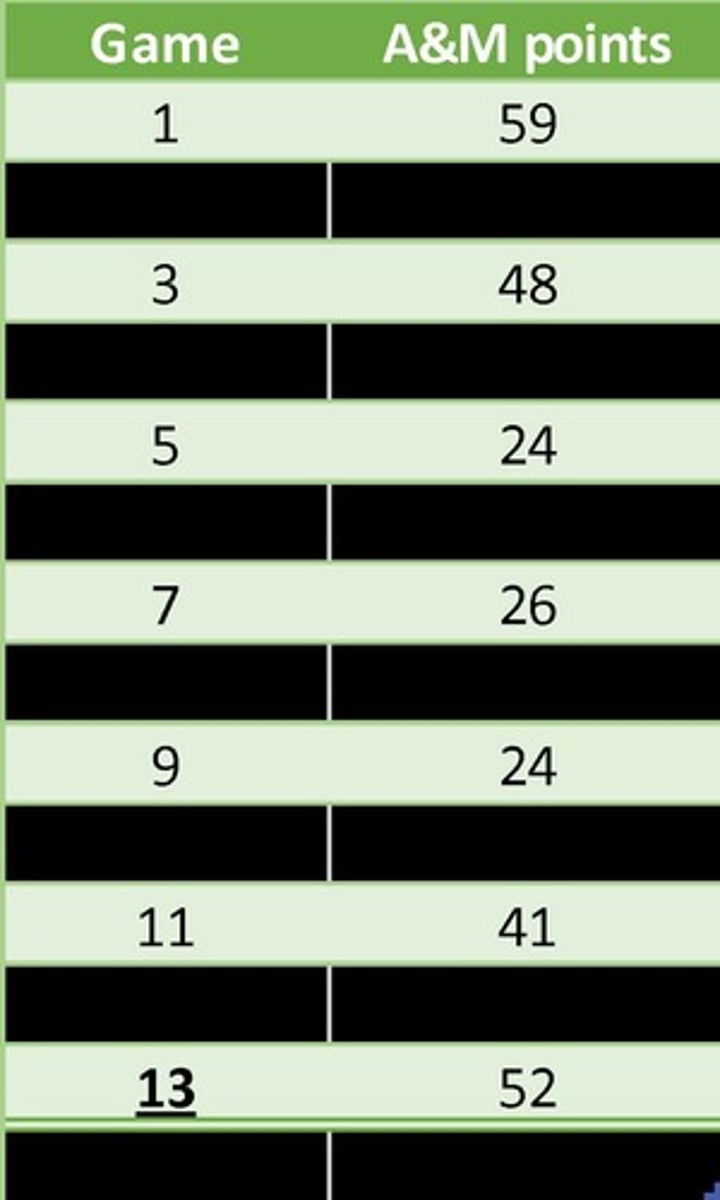
Mean Sensitivity

The mean is sensitive to extreme scores, which can skew the representation of the data.

Typical Value

A value that best represents an entire set of scores.

Exam Average Interpretation

If the average score on an exam is 90 out of 100, it reflects the typical performance of the test-takers.

Sample Size

The number of observations in a dataset, which can affect statistical calculations.

Data Distribution

The way in which data values are spread or arranged.

Income

$50,000

Distribution

The distribution is skewed to the left (negative skew).

MLB player's annual salary in 2016

Mean of more than 4 million, median of 1.2 million

Top 5 players

Clayton Kershaw $34,571,428, Zack Greinke $34,000,000, David Price $30,000,000, Miguel Cabrera $28,000,000, Justin Verlander $28,000,000

Finding the mode

No formula or trick to finding the mode; just count up how many times each value appears.

Mode Usage

Typically used with nominal (categorical) data.

Favorite Baseball Team

Astros 150, Rangers 200, Royals 72, Yankees 4

Range

The most general measure of variability; computed by subtracting the lowest score from the highest score.

Range Formula

r = h - l, where r = range, h = highest score in data set, l = lowest score in data set.

Interquartile Range (IQR)

The distance between the 75th and the 25th percentile scores.

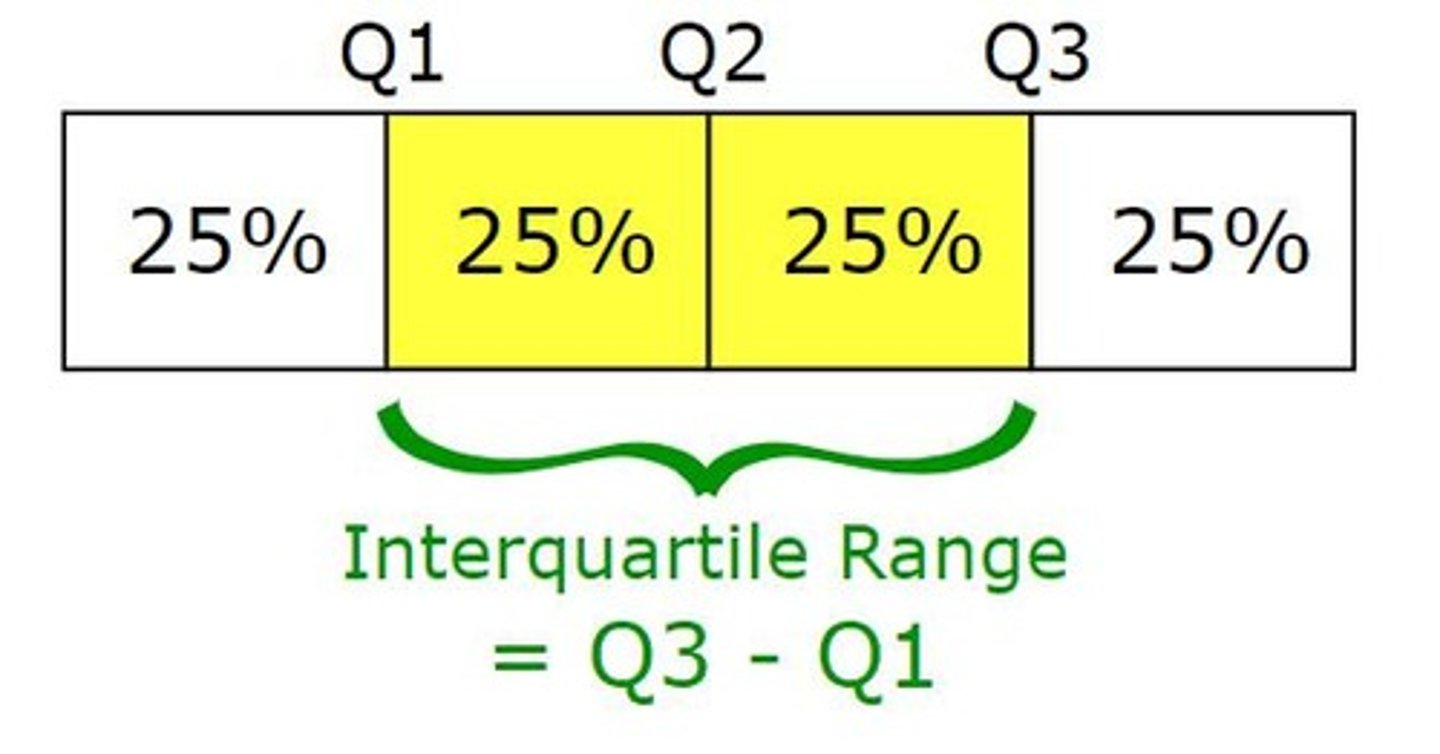
Percentile

A percentile score is a score at which X% of the scores recorded are below that score.

Standard Deviation

The most frequently reported measure of variability; represents the average amount of variability in a set of scores.

Sum of squares

This is known as the sum of squares.