Natural Deduction process + rules

Parts of a Proof

• Horizontal line

  • written below the premieses

  • put conclusion and assumptions, other rules below

• Scope line / vertical line

  • Tells you which assumptions are alive and which you got rid of

  • some premises will be alive for entire proof (line spanning all the way down)

  • some you just have to make assumption for proof (get rid of before end)

Introduction rules

• allows is to prove a sentence that has that connective as the main logical operator

• prove from nothing

Elimination rule

• allows us to derive parts of a sentence that have that MLO

• you are given a sentence with that MLO, prove other sentence

Citing lines

• on every line you have to justify why you got it

• cite relevant lines above using line numbers

  • if you have a subproof it will be a ‘-’, sometimes there are multiple numbers or sets of numbers, separate by comma as well

  • If subproof it will be ex: 1-4, or 1, 1-4 

  • Cite relevant lines that are above

How to cite an individual line when applying a rule

1. the line must come before the line where the rule is applied

but

2. the line must not occur within a subproof that has been closed before the line where the rule is applied

• You have to do the whole entire subproof before you can cite it, also do not close a subproof before you can cite where the line is

You cannot refer back to anything that was obtained using discharged assumptions

To make a subproof

• draw a scope line under previous lines

• draw a horizontal line to make your assumption

• do it

• to close it just end line, end lines will be longer and longer until the last one

To cite a subproof when applying a rule

1. The cited subproof must come entirely before the application of the rule where it is cited

2. The cited subproof must not lie within some other closed subproof which is closed at the last line it is cited

3. The last line of the cited subproof must not occur inside a nested subproof

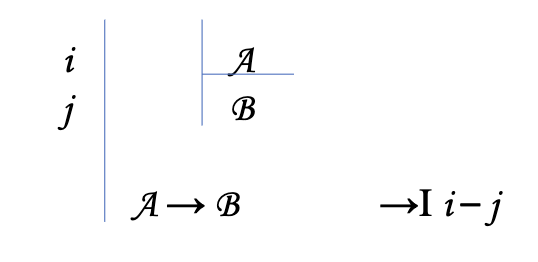
Biconditional Introduction  (↔ I)

• you need two subproofs

• the antecedent proving the consequent and the consequent proving the antecedent

• doesnt matter what line you derive from what first

Ex: A ↔ B 

Need to prove A→ B 

And B → A 

To cite: cite subproof 1 with dash between 1st and last line of subproof, comma, cite subproof 2

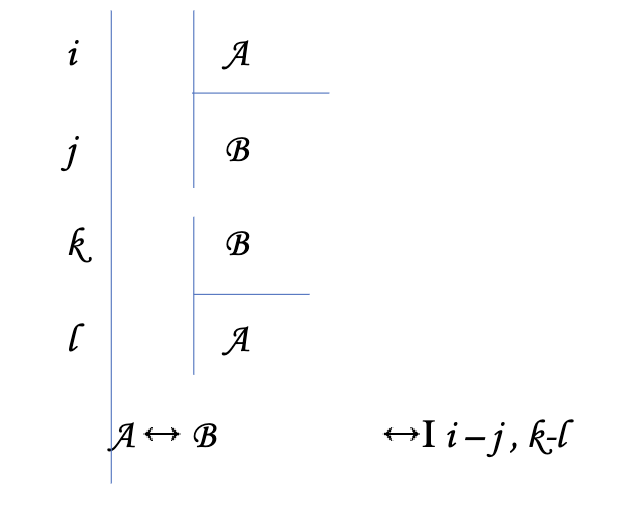
Biconditional Elimination  (↔ E)

• If you have one letter in the biconditional you can get the other

Ex: if you have A ↔ B

• you can get A if you already have B

• you can get B if you already have A

To cite : Cite the line of the full/original biconditional, then the line of whatever letter you got first (think of as antecedent, although it can go both ways)

Disjunction Introduction (V I)

• If you have one disjunct/letter, and you want to create a disjunction, you can assume anything you want as another disjunct

• Can OR on anything you want (A, B, whole other sentence, etc.)

Ex: A 

A V (B, X, i.e) 

To cite: Only have to cite the number of the base/original disjunct, the letter you are adding something to

• inclusive or, assume base is true, anything you put on is true as a result

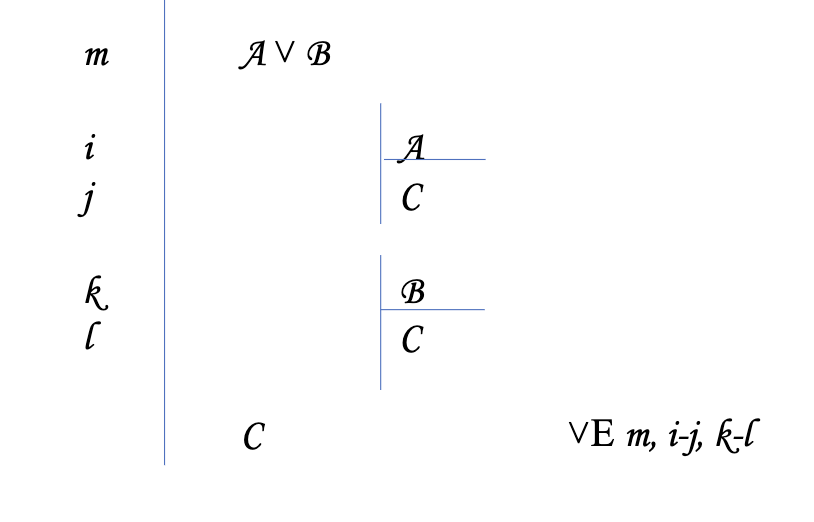
Disjunction Elimination (V E)

• Two subproofs

• each disjunct has to prove the conclusion for conclusion to be true

Ex: A V B ⊢ C

• A has to prove C

• B has to prove C 

Subproofs

• If A then C

• If B then C

  • kind of like mini conditionals

To cite: original/full disjunct, subpoof 1 with dash to first and last line, comma, subproof 2 citation

Negation Elimination (¬ E)

• If you prove a sentence and the negation of that sentence

• you can cite/justify the line with a contradiction by negation elimination

Ex:

¬ A

——

A

⊥

Cite: E original line, contradiction of line

could be negation first or regular first, it depends which one comes first, which one is the contradiction of og

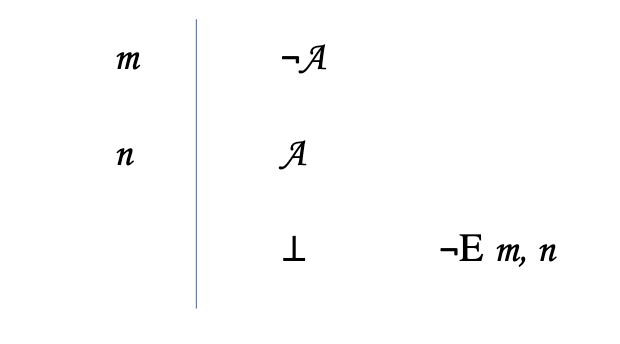
How to get contradiction ⊥

• Prove any sentence and the negation of that sentence

“ ⊥ ” is the symbol that means something like “contradiction!”.

• It is an atomic sentence that can only take the value F. 

Negation is truth preserving

Negation Introduction ( ¬ I )

• show assumption leads to a contradiction, after getting ⊥ you can prove the negation of the assumption

Ex:  you assumed B in subproof and got a contradiction, you can then get conclusion ¬ B using negation intro

• Introduce opposite of sentence after you have proved contradiction

To cite: I the first line of subproof to the last line/contradiction. - proves that it's the opposite so you can introduce the opposite of the og/first line which is its 

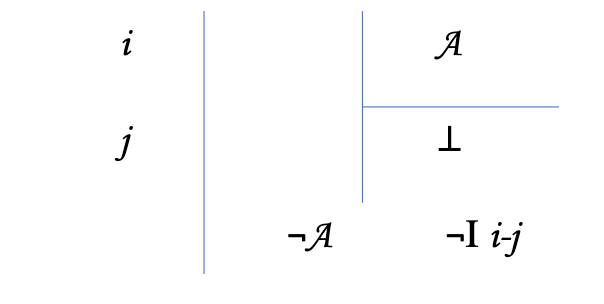
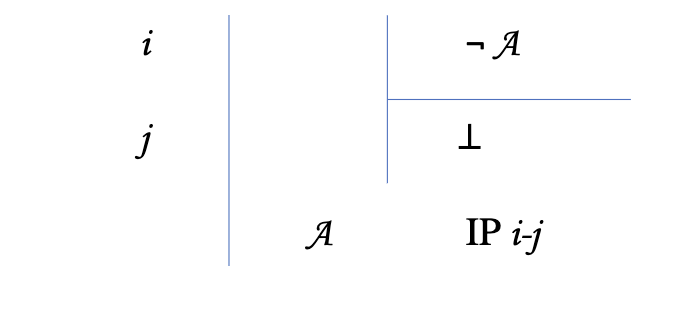
Indirect Proof (IP)

• Assume the opposite of what you have , and try to prove a contradiction so you can get original thing

• If you want to get A, assume ¬ A in subproof and then get contradiction

¬ A

—-

⊥

A

To cite: IP first line of subproof - last line of subproof

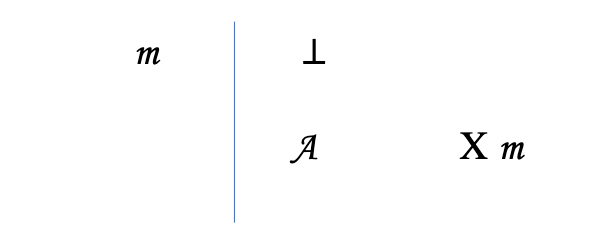
Explosion (X)

• If you get a ⊥ you can assume/derive anything from it

• Elimination rule for contradiction

• truth preserving in a vacuous way (If your premises are contradictory you should be able to derive any conclusion you want and the argument will be valid logically )

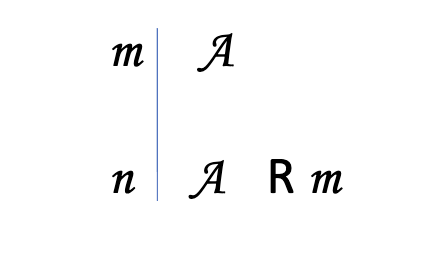
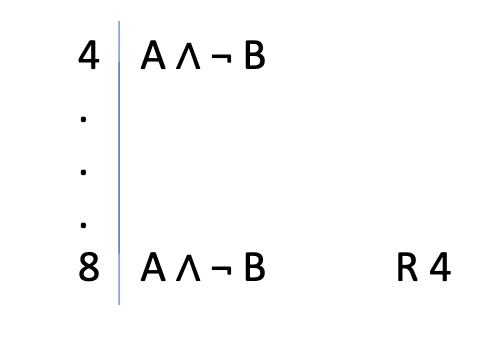
Reiteration Rule (R)

• Allows us to repeat a line already shown in the proof

Ex:

A

A

Cite: line where it was shown before

Strategy for acing proofs

1. Required - start by listing any premises, if any

2. Identify the main connective of each of the starting assumptions/premises

   • purpose- the MLO tells you what elimination rule you can apply first to each assumption

3. Apply any non-subproof elimination rules to your assumptions

   • Purpose- Make the sentences you can infer from the starting assumptions available for the rest of your proof

4. Identify the main connectives in the conclusion

   • purpose - the MLOs tell you what rule you will most likely apply first in order to prove the conclusion

5. Use rules that allow you to introduce connective in the conclusion

   • purpose - allows you to build the conclusion up from the lines of the proof

   • aim to add smaller subsentences of the conclusion to the proof before more complex ones

   • if introducing a connective requires a subproof, start subproofs for introducing wider scope connectives before ones introducing narrower scope connectives

Conjunction Introduction (∧ I)

• If you have the two conjuncts by themselves you can and them together to get a conjunction using introduction

Ex:

A

B

A ∧ B

To cite: line numbers where both of the original conjuncts are, seperate with comma

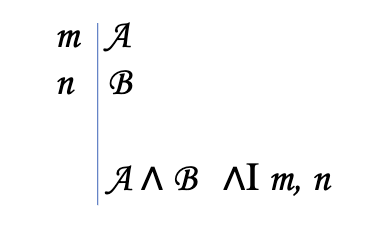
Conjunction Elimination (∧ E)

• You can get each of the conjuncts on its own from a conjunction using ∧ elimination

Ex:

A ∧ B

A

B

Cite: the line where the original/base conjunction sentence is (where you are getting each of the conjuncts from)

Conditional Elimination (→ E)

• when you have a conditional and its antecedent, you can get its consequent

  • if the antecedent is true, the consequent/conditional has to be true

Ex:

A→ B

A

B

Cite: line where you find original conditional, line where you find antecedent

Conditional Introduction (→ I)

• introduces conditional showing that A follows from B in its own proof (subproof)

• create a subproof

  • where you assume the antecedent and derive the consequent

  • then conditional statement has to be true

Subroof

A

—-

B

A → B

Cite it : number of first line of subproof (antecedent) to (dash), number of last line of subproof (consequent)