Physics-topic 8 Waves and particle nature of light

Amplitude

A wave’s maximum displacement from the equilibrium position

Frequency (f)

the number of complete oscillations passing through a point per second

Period (T)

the time taken for one full oscillations

Speed (v)

The distance travelled by the wave per unit time

Wavelength

The length of one whole oscillation (e.g. the distance between successive peaks/troughs).

Wave speed equation

v=flambda

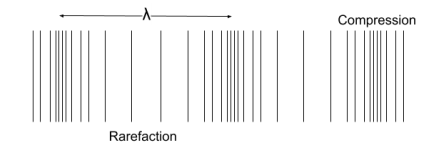
Longitudinal wave

• the oscillation of particles is parallel to the direction of energy transfer

• These are made up of compressions and rarefactions and can’t travel in a vacuum

• Sound is a example of a longitudinal wave, and they can be demonstrated by pushing a slinky horizontally

Longitudinal wave picture

Transverse wave

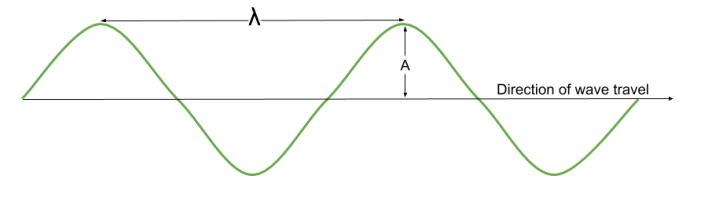
• the oscillations of particles (or fields) is at right angles to the direction of energy transfer

• All electromagnetic waves are transverse and travel at 3 c 10^8 m/s in a vacuum.

• Transverse waves can be demonstrated by shaking a slinky vertically or through the waves seen on a string, when it’s attached to a signal generator

Transverse waves picture

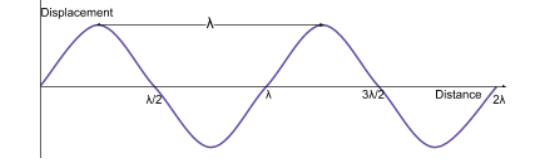
Displacement-distance graphs

these show how the displacement of a particle varies with the distance of wave travel and can be used to measure wavelength

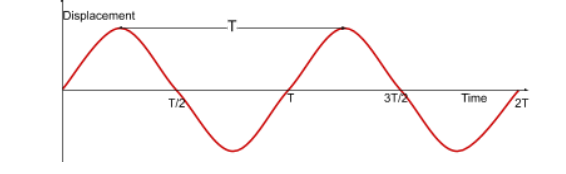
Displacement-time graphs

these show how the displacement of a particle varies with time and can be used to measure the period of a wave

Phase

The position of a certain point on a wave cycle. This can be measured in radians, degrees of fractions of a cycle

Phase difference

How much a particle/wave lags behind another particle/wave. This can be measured in radians , degrees or fractions of a cycle

Path difference

The difference in the distance travelled by two waves

Superposition

Where the displacements of two waves are combined as they pass each other, the resultant displacement is the vector sum of each wave’s displacement

Coherance

A coherant light source has the same frequency and wavelength and a fixed phase difference

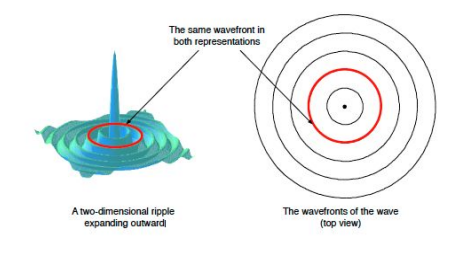
Wavefront

a surface which is used to represent the points of a wave which have the same phase

Wavefront example

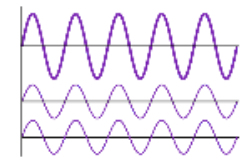
Constructive interference

this occurs when two waves are in phase and so their displacements are added (occurs during superposition)

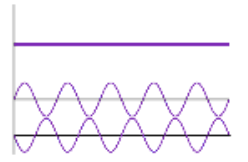
Destructive interference

this occurs when the waves are completely our of phase and so their displacements are subtracted (occurs during superpositions)

Constructive interference picture

Destructive interference picture

In phase

Two waves are in phase if they are both at the same point of the wave cycle, meaning they have the same frequency and wavelength and their phase difference is an integer multiple of 360 degrees.

completely out of phase

Two waves are completely out of phase when they have the same frequency and wavelength and their phase difference is an odd integer multiple of 180 degrees

phase difference equation

change in x /(lambda/2pie)change in phase difference where x is path difference

Stationary wave

formed from the superposition of 2 progressive waves, travelling in opposite directoins in the same plane, with the same frequency, wavelength and amplitude

Is energy transferred by a stationary wave?

No

Where waves meet: in phase

constructive interference occurs so antinodes are formed, which are regions of maximum displacement

Where waves meet: completely out of phase

destructive interference occurs and nodes are formed, which are regions of no displacement

Example of how a stationary wave is formed?

A string fixed at one end; and fixed to a drving oscillator at the other gives a good example of the formation of a stationary wave:

• A wave travelling down the string from the oscillator will be reflected at the fixed end of the string, and travel back along the string causing superposition of the two waves. Because the waves have the same wavelength, frequency and amplitude, a stationary wave is formed

Speed of a transverse wave on a string

v=root T/u where T is tension and u is the mass per unit length of string

Intensity

the power per unit area

Intensity equation

I=P/A

Refractive index

a property of a material which measures how much it slows down light passing through it. A material with a higher refractive index can also be known as being more optically dense

Refractive index equation

n=c/v where c is speed of light in a vacuum and v is speed of light in that substance

Refraction

occurs when a wave enters a different medium, causing it to change direction, either towards or away from the normal depending on the material’s refractive index

Snell’s law

n1sinx1=n2sinx2

Snell’s law picture

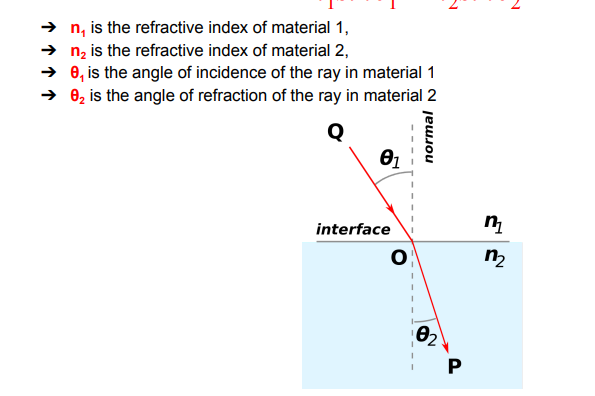
Critical angle equation

sin C= 1/n where n>1

When does total internal reflection (TIR) occur

when the angle of incidence is greater than the critical angle and the incident refractive index (n1) is greater than the refractive index of the material at the boundary (n2)

Converging lens

these are curved outwards on both sides and cause parallel light rays to move closer together/ converge at a point

Diverging

these are curved inwards on both sides and cause parallel light rays to move apart/diverge

Principle focus (F) in a converging lens

the point at which the light rays which are parallel to the principle axis are focused

Principle focus (F) in a diverging lens

the point from which the light rays appear to come from

Focal length (f)

the distance from the centre of the lens to the principle focus

Power

the measure of a lens’ ability to bend light. In converging lenses this value is positive and in diverging lenses this value is negative

Power equation

Power = 1/f

What is a thin lens

a lens with a thickness which allows rays to light to refract but not experience dispersion or aberrations

Real image

one which can be projected onto screen as light rays reach the image location

Virtual image

one that cannot be projected onto a screen