Skewness & kurtosis

Skewness & kurtosis

Skewness

• measures the asymmetry of the data distribution and helps us to understand how values are spread around the mean.

• describes the shape & direction of the skew (right or left)

• sensitive to the changes of the tails in the distribution.

Three types of skewness

• normal distribution - no skew (median=mode=mean)

• left skewed - long left tail (mean in the left peak, followed by the median in middle, mode at the right peak)

• right skewed - long right tail (mean in the right peak, followed by the median in middle, mode at the left peak)

• left skewed

• longer than the right side

• mean is less than the median

• mode is greater than both median and mean

• negative distribution

• right skewed

• longer than the left side

• positive distribution

• mean is greater than the median, which is greater than the mode.

if the majority of the extreme values will be higher than the mean

• the skewness is right, and will be positive

• (we increase the mean)

if the majority of the extreme values will be lower than the mean

• the skewness is left, and will be negative

• (we decrease the mean)

Kurtosis

• measures the peak or height of the data distribution & helps us understand the shape of frequency distribution.

• measures “tailedness” of the distribution

• describes the shape of the distribution´s peak & tails

• sensitive ti changes in the centre

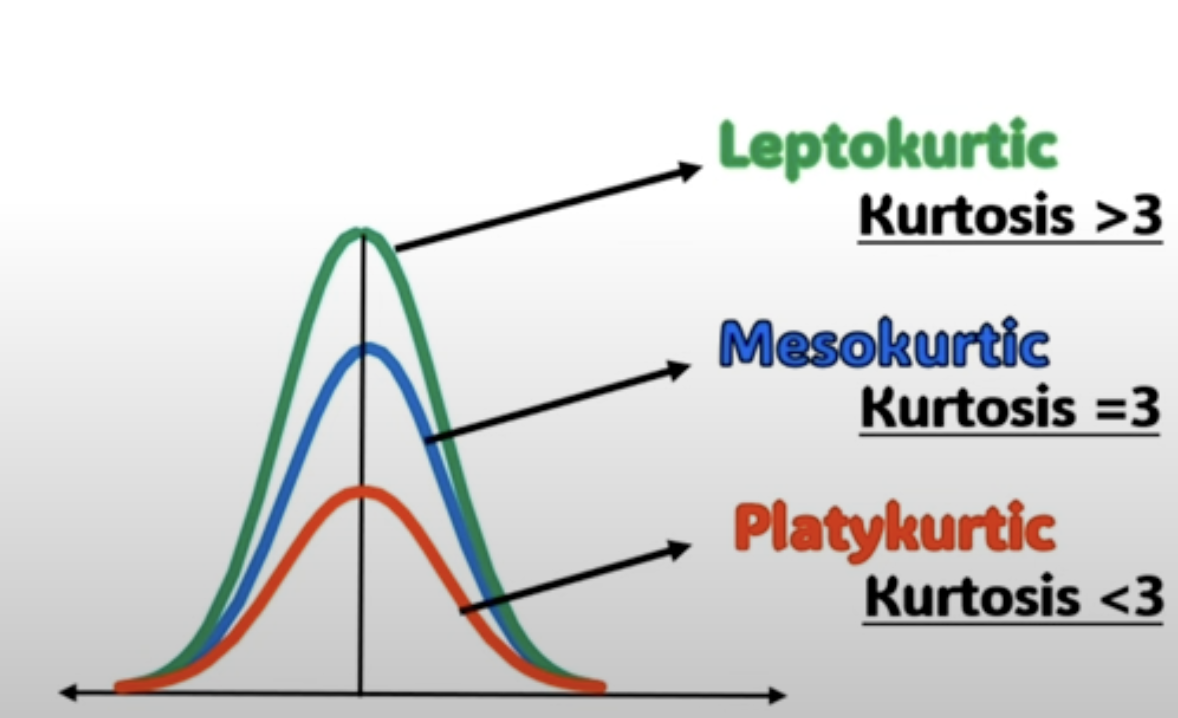
Three different types of kurtosis

• Mesokurtic

• Platykurtic

• Leptokurtic

Mesokurtic

• normal distribution

• Kurtosis equals 3

Platykurtic

• value less than 3

• the curve has a lower peak than the normal distribution/mesokurtic curve

• less distributions of items around the central value/ mean

Leptokurtic

• value is greater than 3

• the peak is higher than the normal distribution

photo of kurtosis distributions