Financial Markets

CML

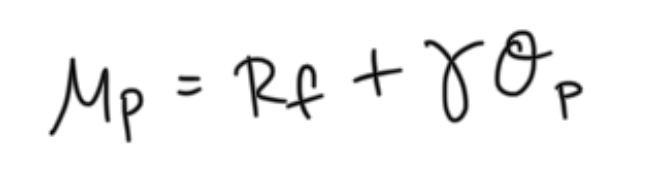
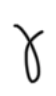
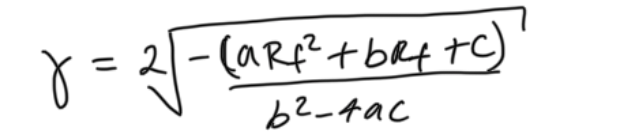
market expected return

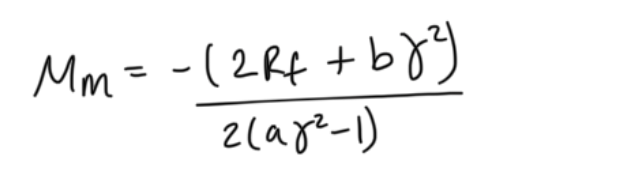
beta

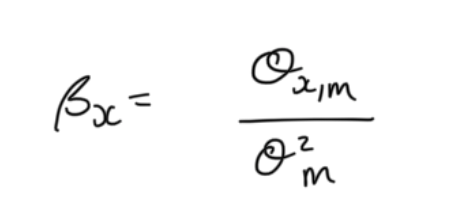
ARA

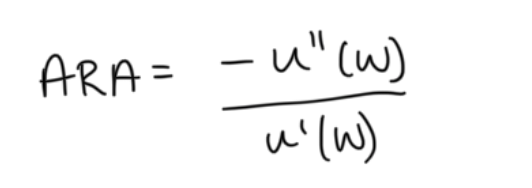
continuous return from discrete

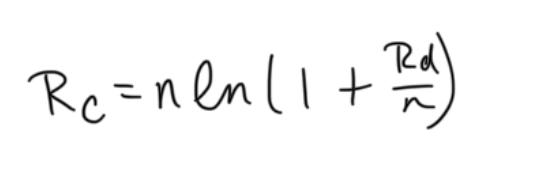
duration

change in price using duration

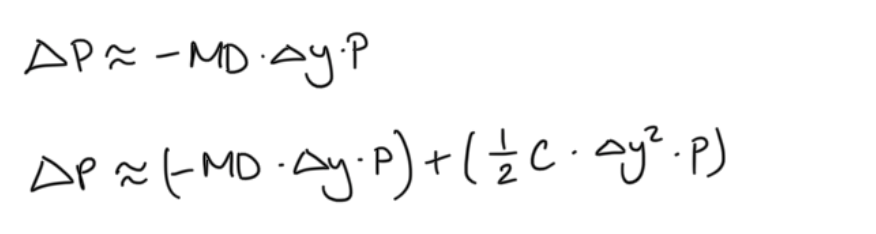
convexity using discrete compounding

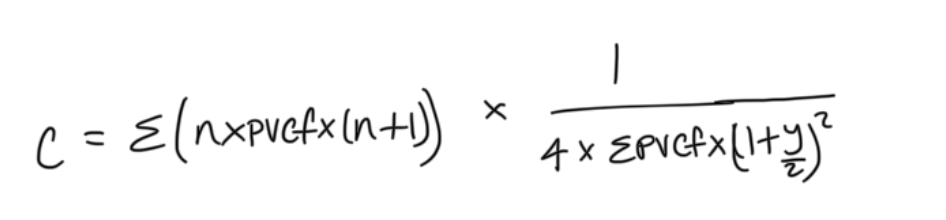
convexity using continuous compounding

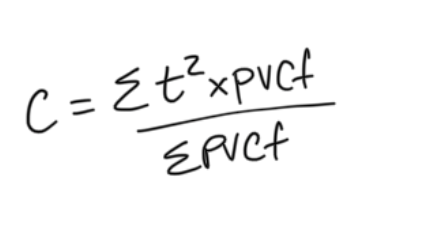
hedge ratio

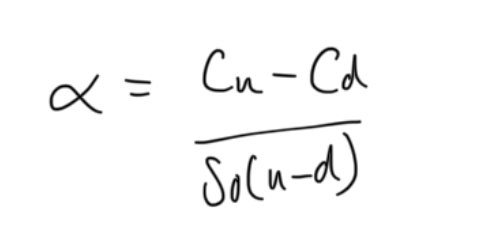
Pseudo probability, p

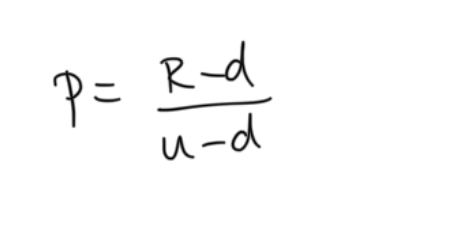
price of call option

min. number of ups to get positive payoff

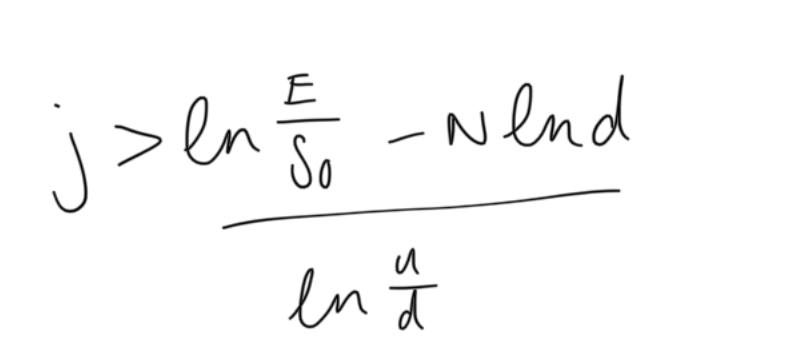
RRA

= ARA*w

amount you would be willing to give up in a fair bet

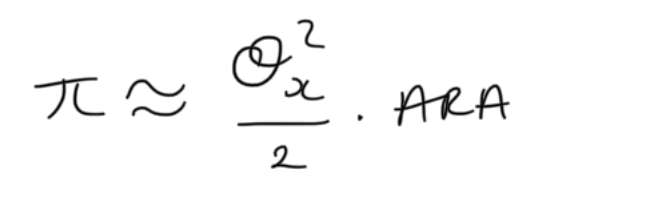
market variance

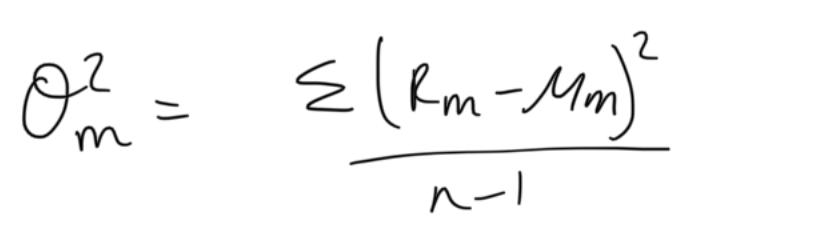
covariance

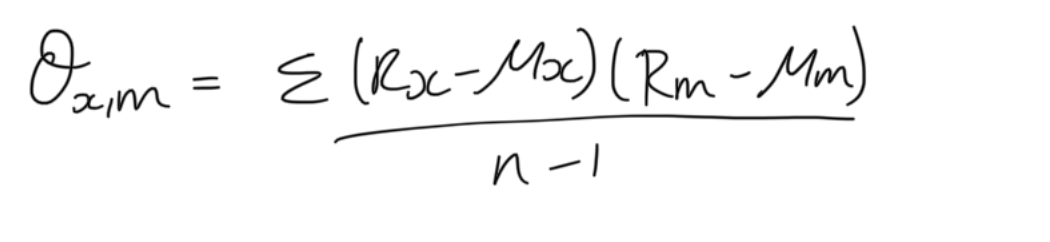
put-call parity

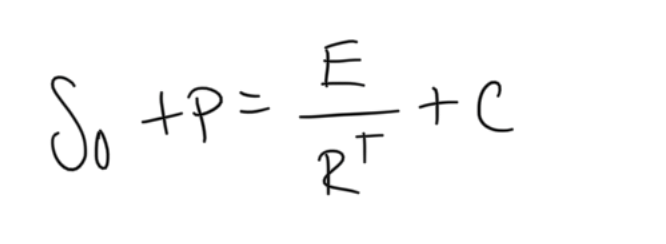
call pricing using binomial approximation

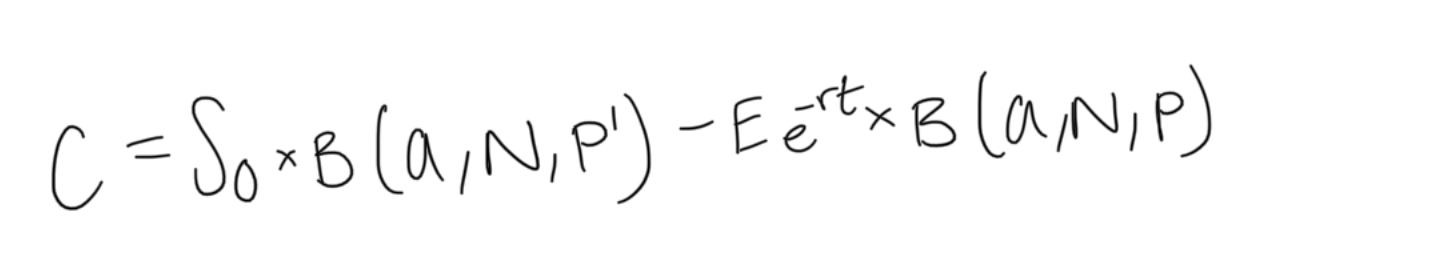
Z₁

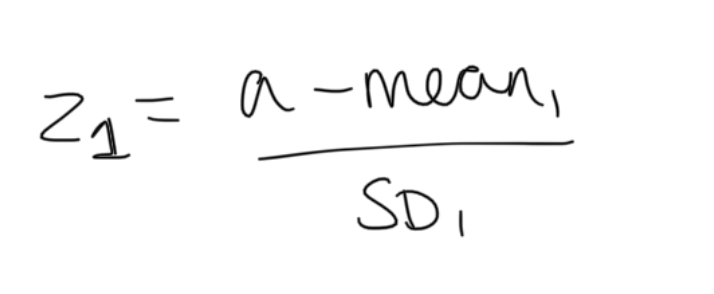
SD₁

P^I

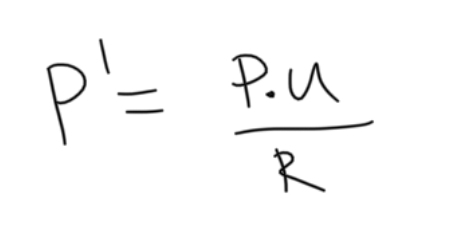
upper bound for call option

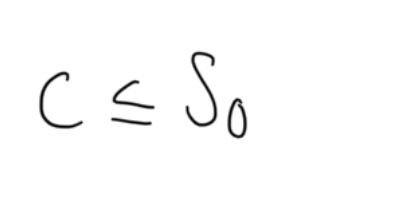
upper bound for put option

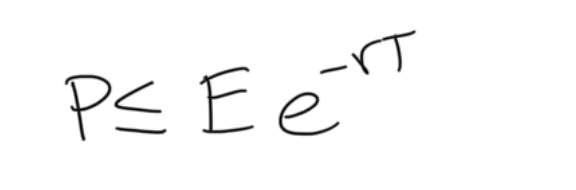
lower bounds of call option

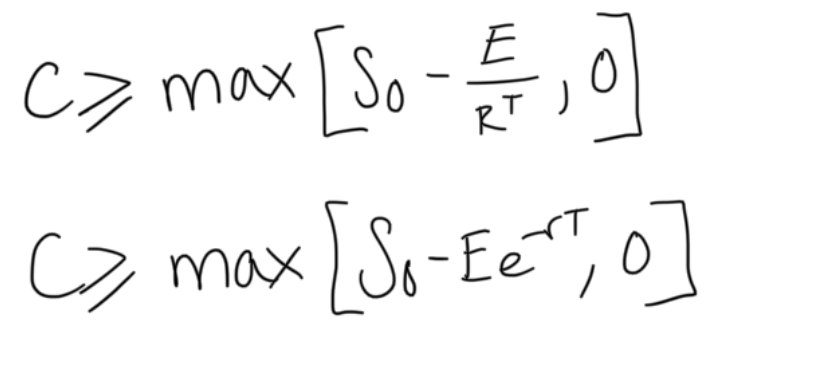
lower bounds for put options

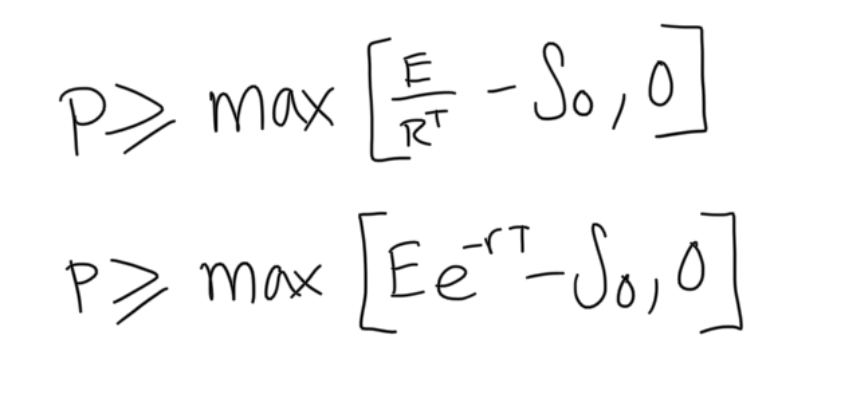
two period binomial option pricing

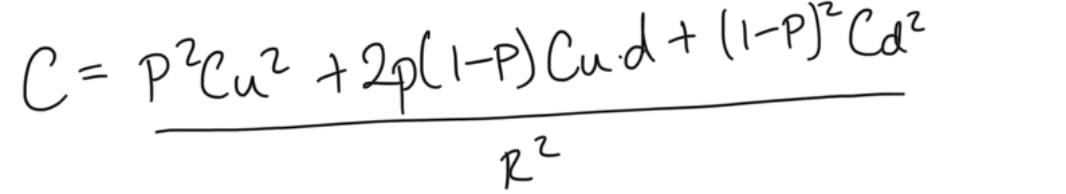
three period binomial option pricing

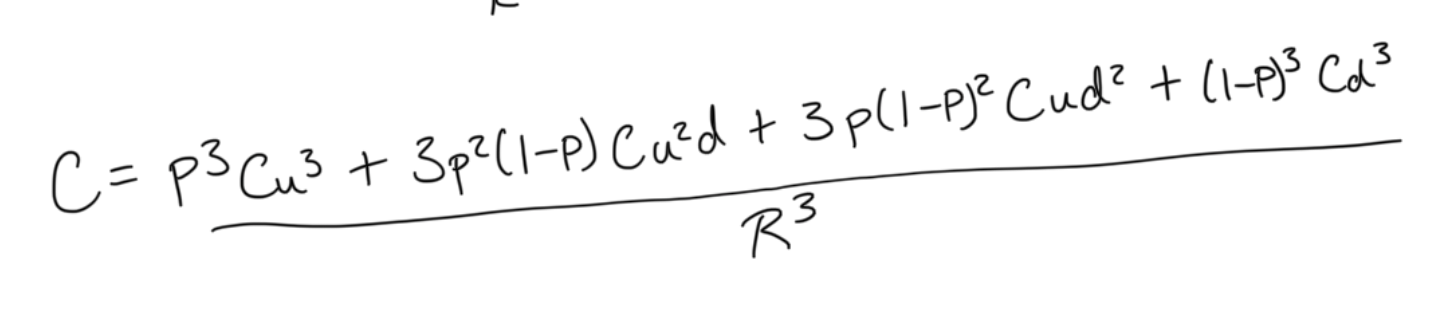
risk neutral probabilities, q

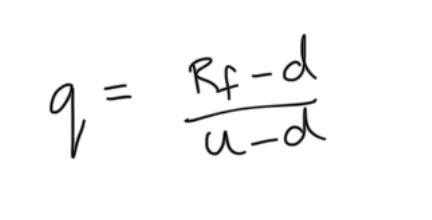
forward prices, no income

forward prices, predictable income

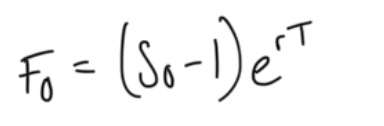
forward prices, predictable yield

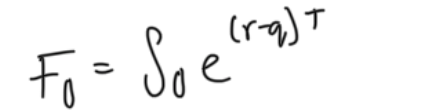
value of long forward

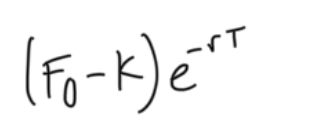
value of short forward

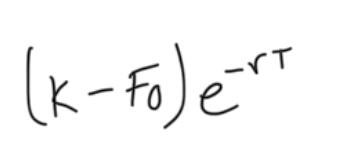
forward rate on currencies

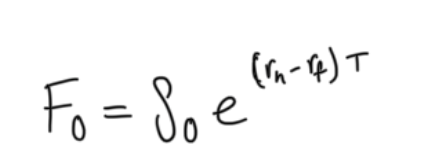
forward rate on investment commodities

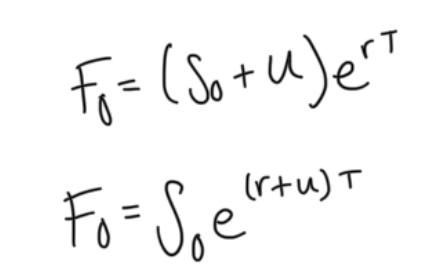
forward rate on consumption commodities

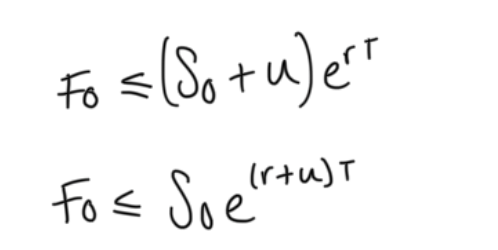
d₁

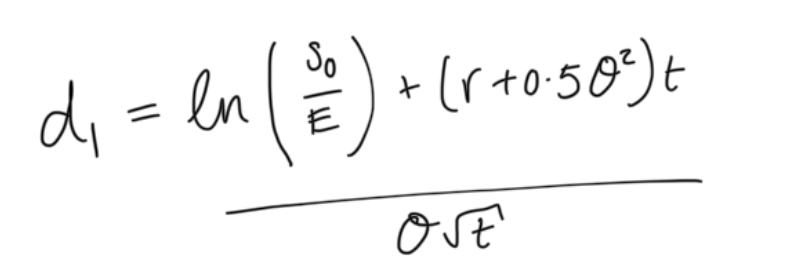
d₂

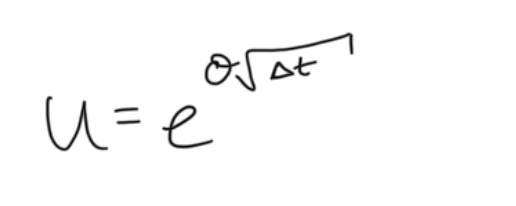
u =

d =

1/u

CAPM Assumptions

• no transaction costs

• all assets are infinitely divisible

• no personal taxes

• markets are purely competitive

• investors choose portfolios purely on expected return and standard deviation

• short sales permitted

• unlimited borrowing and lending at the risk free rate

• investors have homogenous expectations

arithmetic returns

• discrete compounding

• multiplicative cumulation

• non-symmetric reversal in return

• not normally distributed

logarithmic returns

• continuous compounding

• additive cumulation

• reversal in return is symmetric

• more normally distributed

fama French model

• extends CAPM to include two additional factors that capture systemic risk that is not explained by the market alone

• factors: market, size, value

• largely empirical

• explains more of the variation in average returns than CAPM

• empirically supported across many markets and long time periods

• lacks strong theoretical foundations

• interpretations of size and value factors still debated

carhart four factor model

• extends on mama French by adding momentum factor

• strong empirical support: captures size, value and momentum effects

• widely used in performance evaluation

• lacks deep theoretical foundation

• momentum may arise from behavioural biases rather than risk premia

CAPM vs APT

• CAPM is one factor only, APT has multiple factors

• CAPM has market risk only, several system risks priced in APT

• CAPM has weak empirical performance but APT has stronger

• core idea of CAPM = excess returns depend on exposure to market portfolio

• core idea of APT = expected returns are determined by multiple sources of systemic risk. condition of no arbitrage prevents mispricing.

effect of a decrease in market interest rate on utility of borrowers and lenders

• market interest rate = -(1+r)

• a fall in r makes the budget line flatter

• can now access a higher utility curve

• consumers consume more this period and next

effect of a decrease in market interest rate on the present wealth of borrowers and lenders

• pv of future income = income*1/1+r

• as r falls, pv of future income rises

• borrower has negative future net income, lower r reduces the pv of loan repayments, increasing the present wealth of borrowers

• lender has positive future income, lower r reduces pv of returns from lending - present wealth of lenders decreases

strategy for arbitrage

• buy the undervalued option

• short the stock if the option is a call

• buy the stock if the option is a put

• do this without borrowing - borrow cash if necessary

credit default swaps

• derivative contract that transfers credit risk of a borrower from one party to another

• protection buyer pays premium

• protection seller compensates buyer if credit event occurs

• settlement may be physical or cash

• mainly used to hedge credit risk, speculate on changes in credit quality, and improve pricing efficiency between bond and credit markets

• CDS involves counterparty risk, may encourage excessive speculation and can contribute to systemic risk if poorly regulated

Explain the nature and properties of Brownian motion(BM); and explain the relevance of the standard form of scaled BM with drift to the pricing of options

stochastic process with following properties:

• W0 = 0

• independent increments: movements over non-overlapping time intervals are independent

• normally distributed increments

• continuous paths

• stationary increments: distribution depends only on the length of the time interval

• in finance it is used calculate stock prices

  

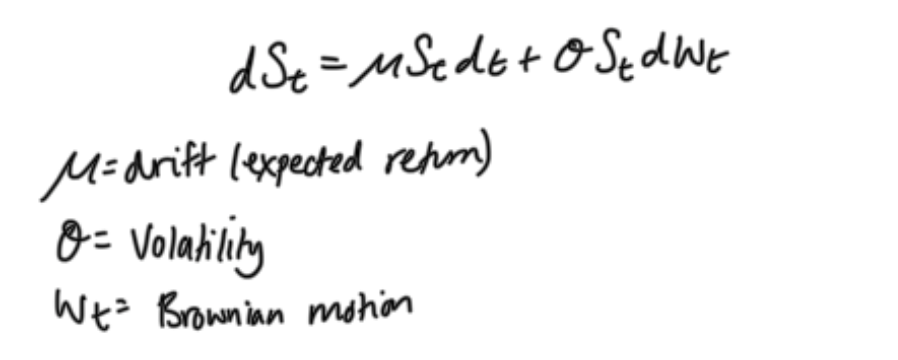
Itos lemma

• applying Ito’s lemma gives the stochastic differential equation for option price

• decomposition separates random part from deterministic part

• by forming a hedged portfolio that eliminates dwt, creating a riskless portfolio

• no arbitrage arguments lead directly to the Black-Scholes partial differential equation

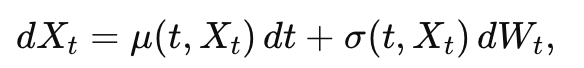
complete vs incomplete market

• complete = every possible payoff across all states of the world can be replicated exactly using traded assets

• incomplete = some contingent payoffs cannot be replicated

redundant assets

• if its payoff can be exactly replicated by a portfolio of other traded assets

• its presence does not expand the set of attainable payoffs

  • removing it does not affect market completeness

Type 1 vs Type 2 arbitrage

type 1 = zero initial cost, non-negative payoff in every state, strictly positive payoff in at least one state

type 2 = negative or zero initial cost, non-negative payoff in every state, weak arbitrage

Arrow-Debreu security

• hypothetical asset that pays 1 unit of consumption in one state of the world, and 0 in all other states

state price vector

• is the vector of prices of all arrow debreu securities

• each element gives the todays price of receiving 1 unit of payoff in a specific state tomorrow