REGENTS GEO

U2Straight angle and supplementary angle

Straight angle = 180 degrees

Supplementary angle = two or more angles that ADD to 18-

U2Reflex angle

More than 180 and less then 360

U2 Perpendicular, right angles

Lines that form right angles

Right angles = 90 degrees

• in proofs, must have “right angle” and “definition of right angle” as separate rows

U2 Negative Angles v positive

clockwise rotation, positive = counterclockwise

• by default = angles rotate counter clockwise

U2 Bisect

Cut into two congruent parts

U2 Skewlines

lines that are non coplanar

U2: Partition Postulate

The whole is the sum of its parts.

• may be used for angle measurments AND lengths

U2 What are the properties of congruence and what do each mean?

Reflexive: figure a is conguent to figure A

Symmetric: Figure A is congruent to fiure B then figure B is congruent to figure A

Transitive: if A is congruent to fig B and fig B is congruent to fig c then fig a is congruent to fig c

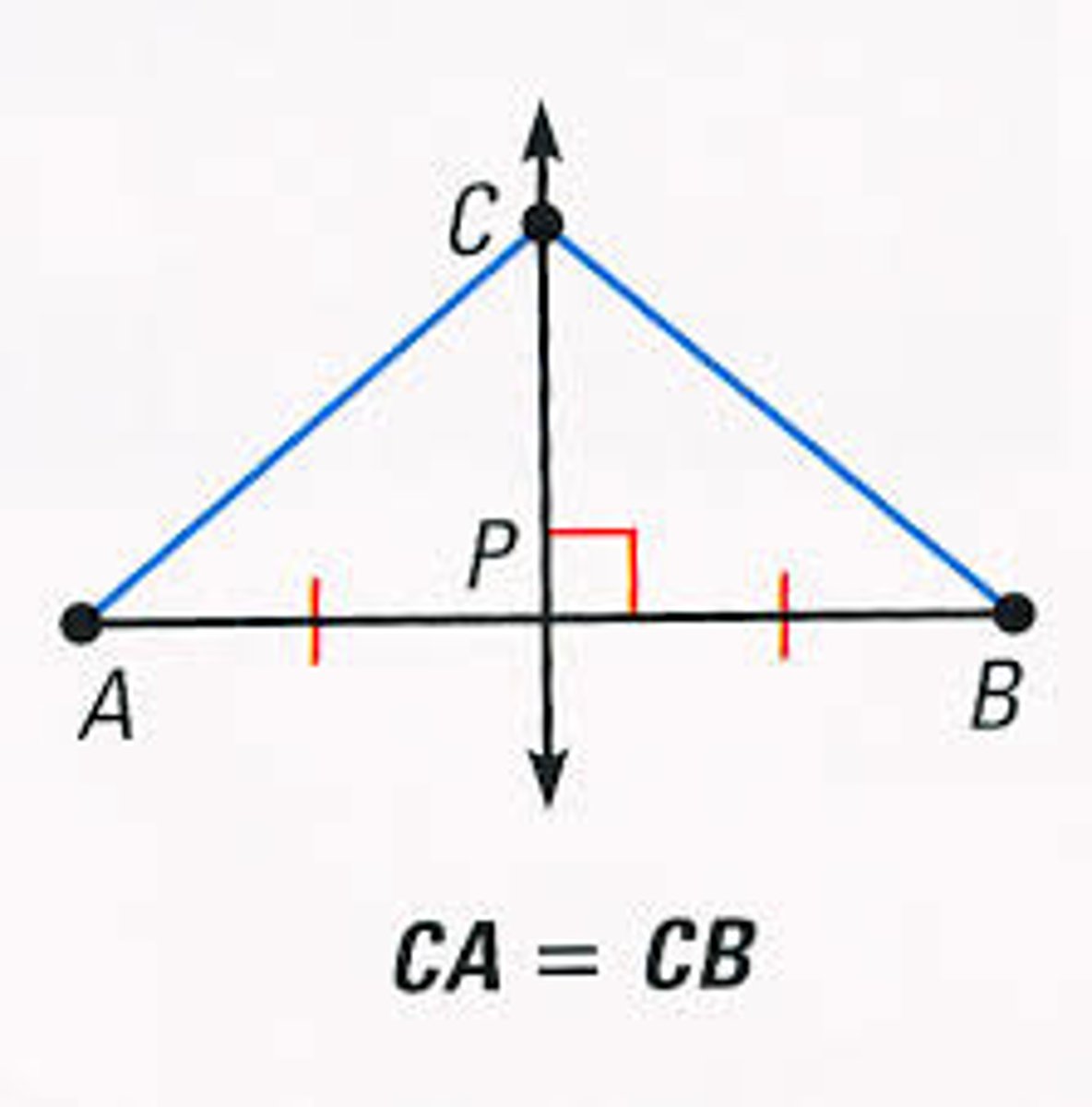
U2 When a way of light is reflected off of a flat surface, the angle of ——- is congruent to the angle of ——-.

Incidence and reflection

U2 Sphere

Collection of points that all have the same distance from a point in the center

U2 Symbols for geometry

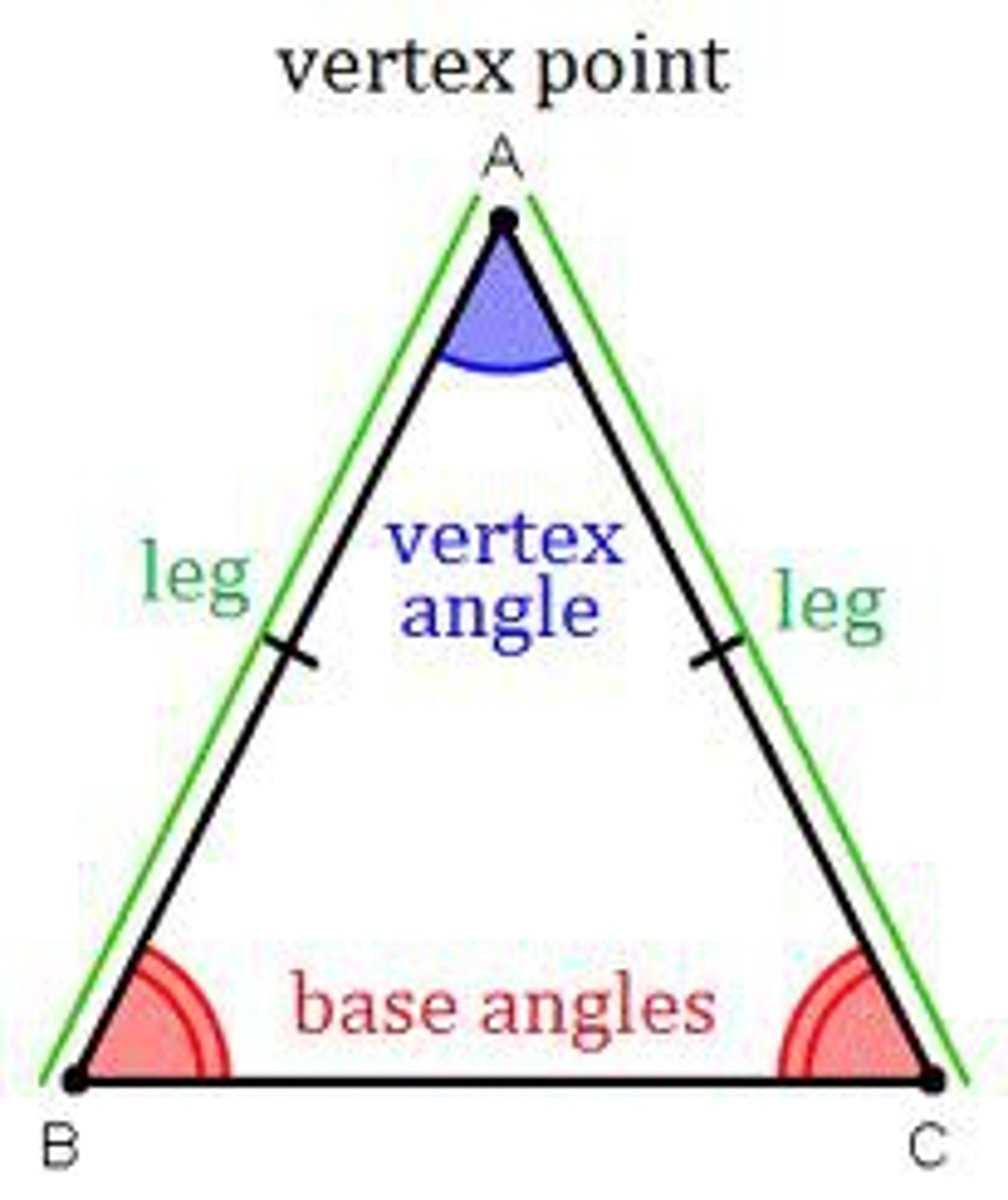
U3: Isosceles Triangle

At least 2 sides are congruent

-2 congruent base sides called legs

-the third side is called the base (between 2 congruent base angles)

• An equilateral triangle can also be calcified as an isoceles triangle because it has “at least” two congruent angles/sides

U3: Two conjectures you can make about isosceles triangles?

Isoceles Triangle Theorem

If two sides of a triangle are congruent then the angles across from those sides are congruent

If two angles of a triangle are congruent then the sides across from those angles are congruent

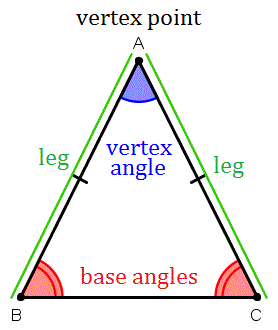
U3: vertex angle of an isosceles triangle and base angle of isoceles triangle

Vertex angle: the angle formed by two congruent sides (angle that doesn't have another angle congruent, the top bit)

Base angle: the angles that are congruent to eachother (not always on the bottom of the triangle)

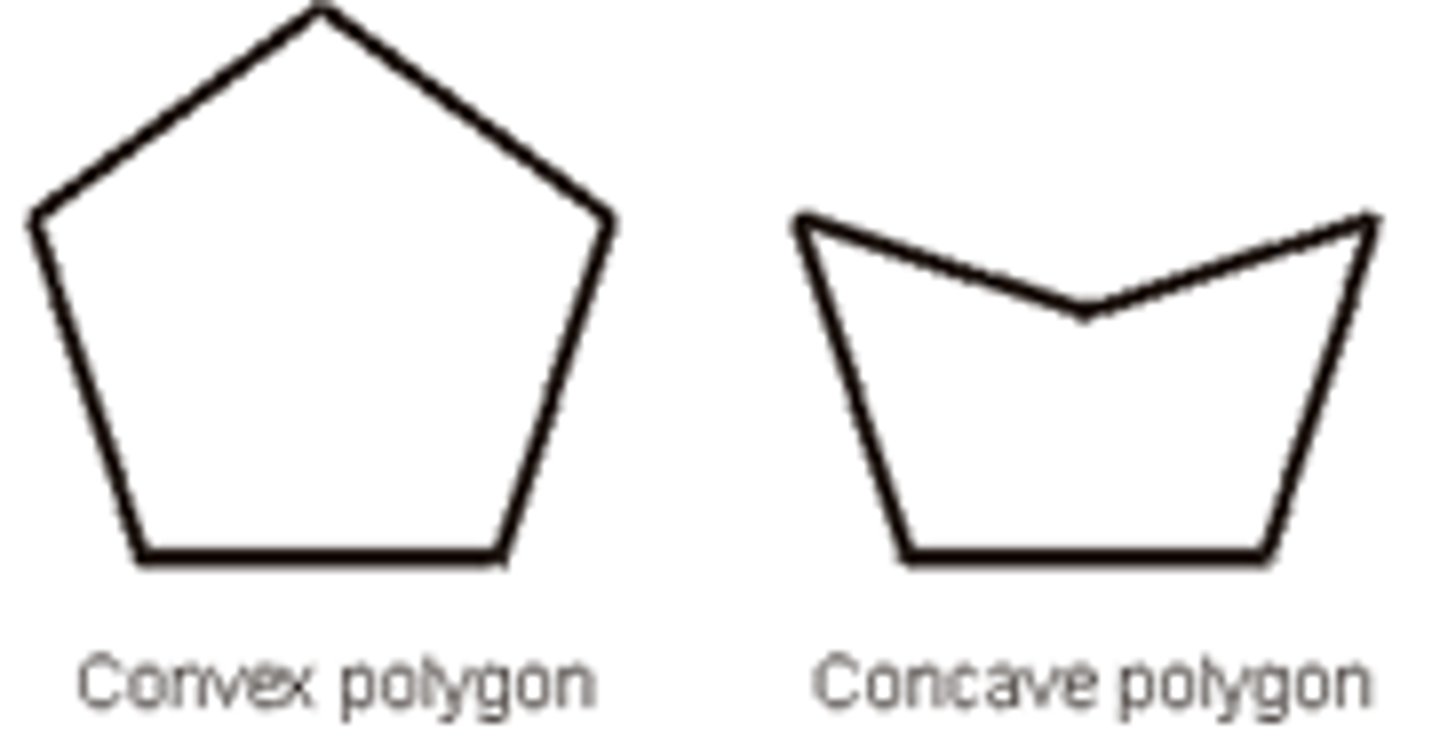
U3: Convex Polygon

A polygon is a convex if and only if...

-it contains all the line segments connecting any pair of points

-each interior angle is less then 180 (no reflexive interior)

-otherwise it is concave

-turn in way

U3: Exterior angle

-the supplement of an interior angle of a polygon

-must form a line (straight) with the interior angle

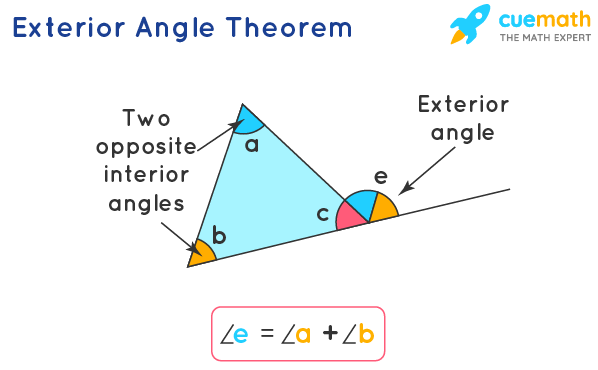
U3: Exterior angle theorem (and how to prove)

The exterior angle theorem states that when a triangle's side is extended, the resultant exterior angle formed is equal to the sum of the measures of the two opposite interior angles of the triangle. The theorem can be used to find the measure of an unknown angle in a triangle.

In this image: Angle e = angle b + angle a

How to prove:

A+b+c=180 interior angles sum of triangles

C+d=180 a straight angle is 180

A+b+c=c+d transitive prop equality

A+b= d subtraction prop of equality

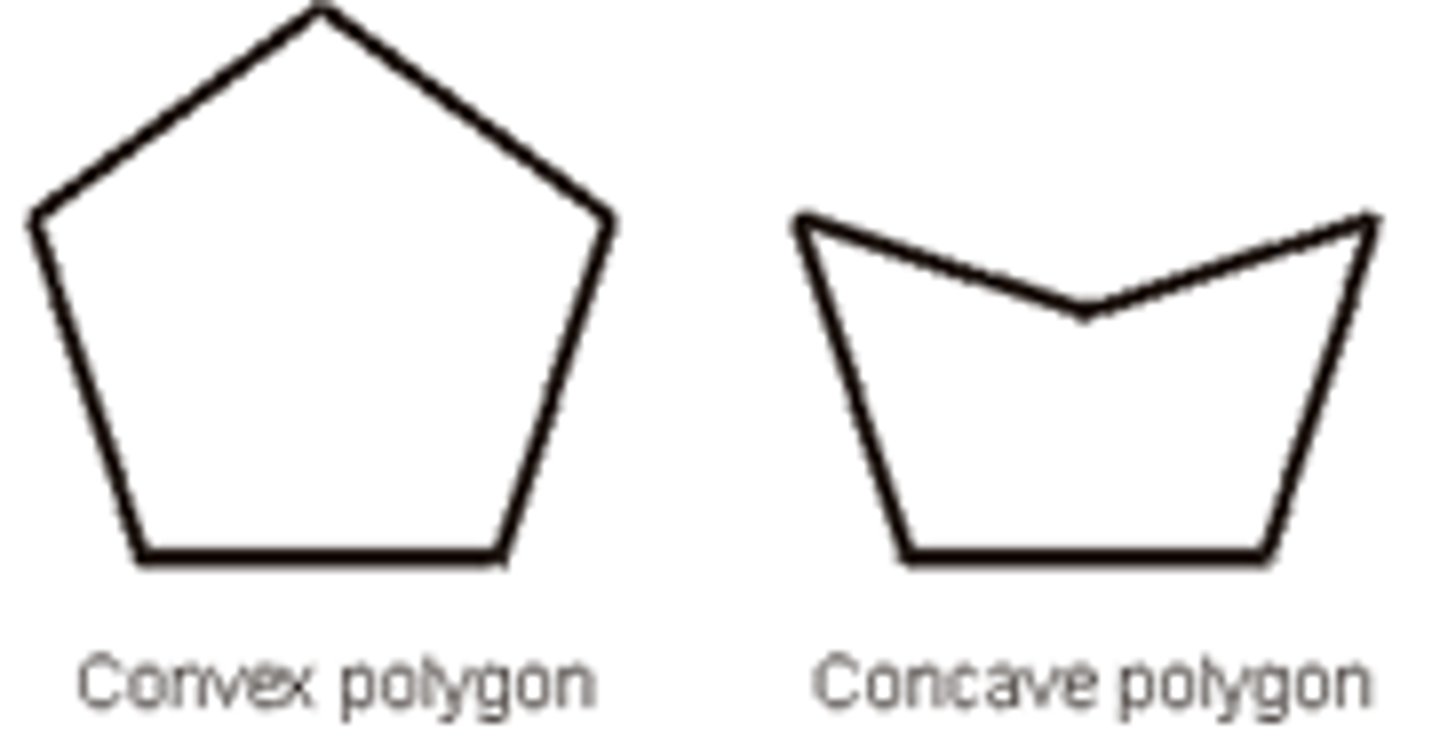
U3: Concave Polygon

-we can draw a segment between any two points OUTSIDE a polygon

-can contain interior reflex angles

-turn more then one way

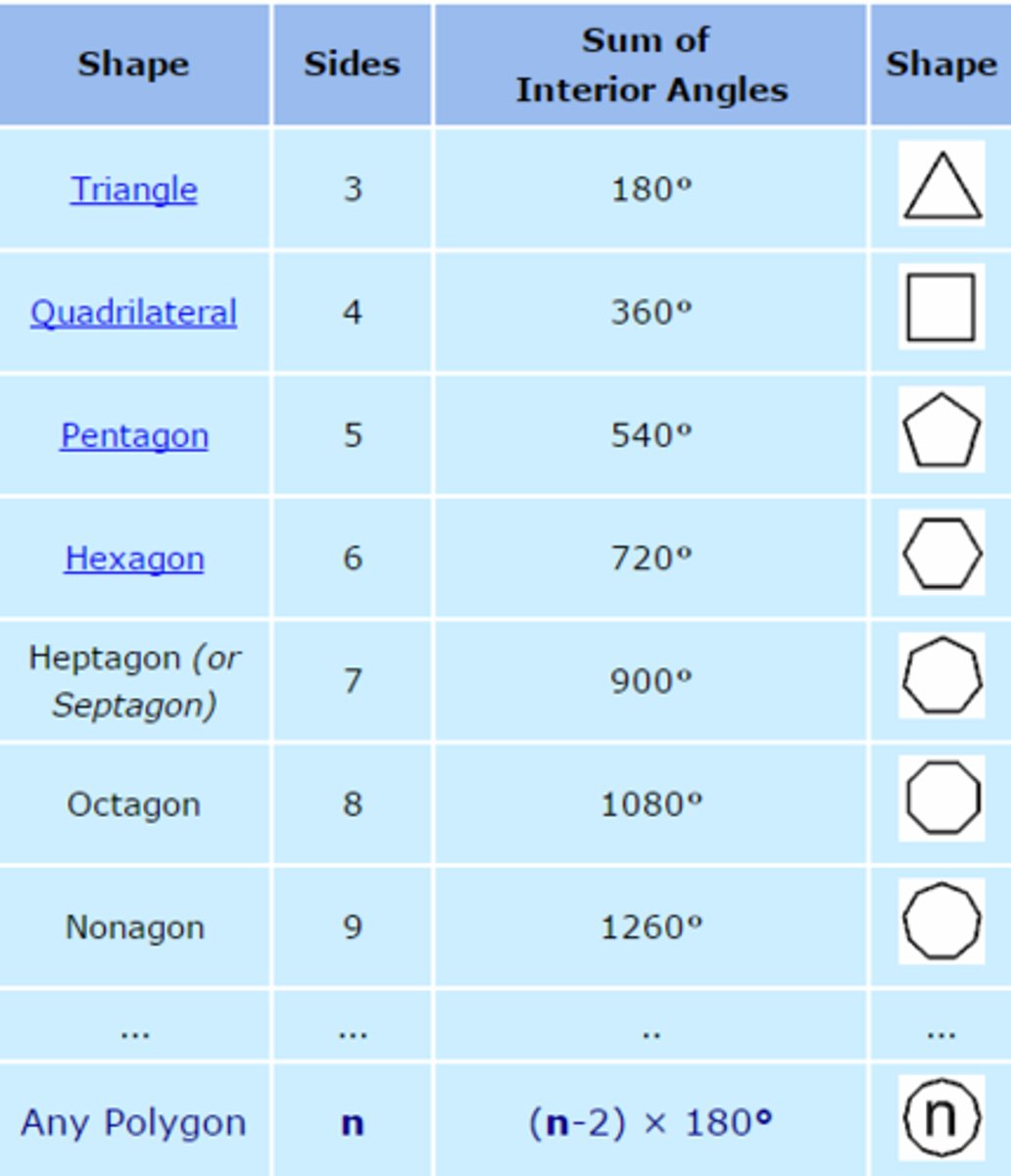
U3: Equation for the sum of interior angles of a polygon (n=number of sides)

(n-2)180

Or all angles - 360 (all angles is n x 180 for all triangles)

U3: Equation for each interior angle

(n-2)180 divided by n

U3: Equation for (each) exterior angle measure and why

360/n

- because 180- ((n-2)180))\n to find supplementary of each interior angle

U3: Transitive property of equality or congruence

If a=b and b=c, then a=c

• different than substutiton because it is between three things/numbers/figures

U3: Name the names of shapes with sides 3-10

3- triangle

4- Quadrilateral

5- pentagon

6- hexagon

8- octagon

10- decagon

U3: Equation for the sum of exterior angles of any polygon

a + b + c + d = 360

The sum of exterior angles of ANY polygon equal 360

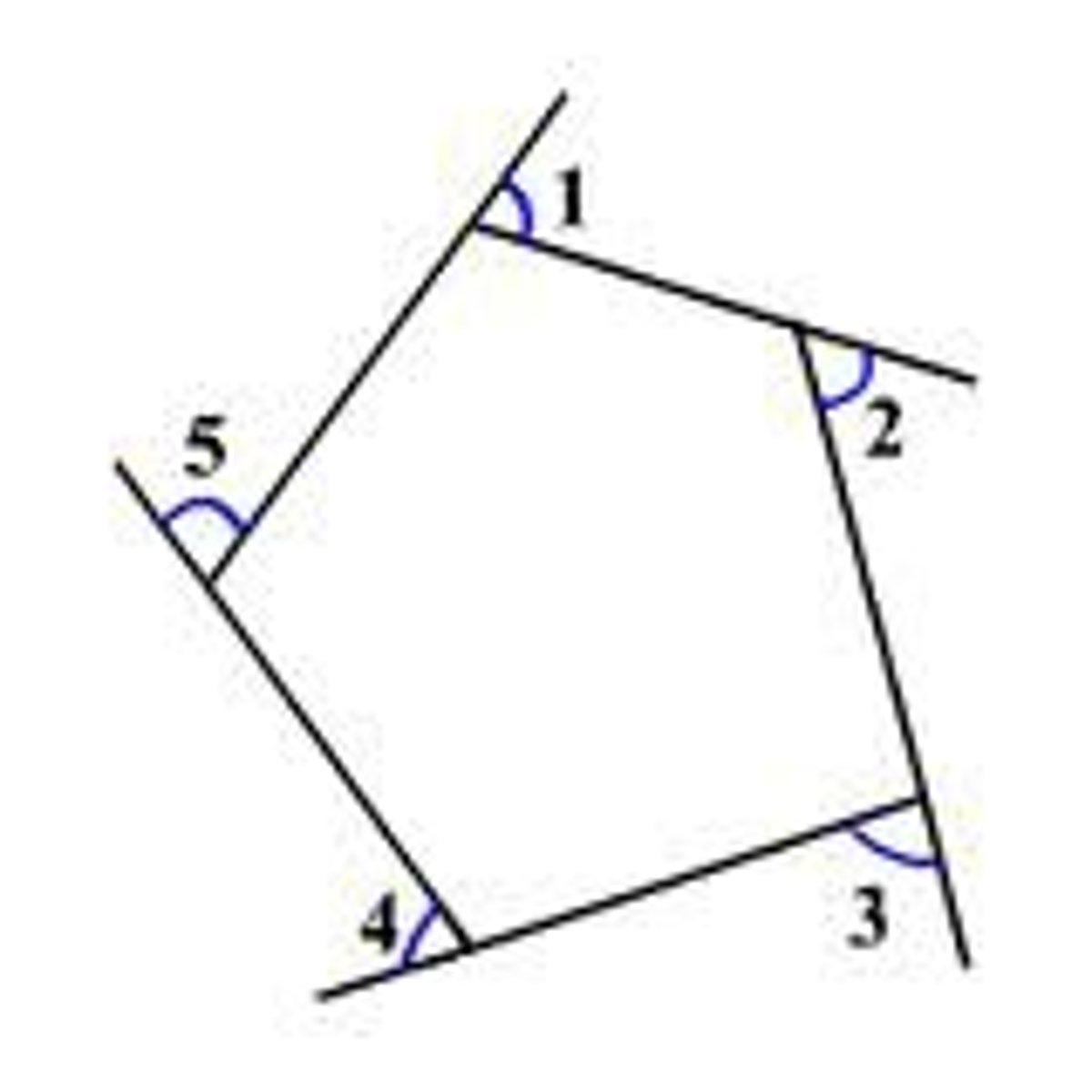
U3: Polygon

A plane figure with at least three straight sides and angles, typically five or more.

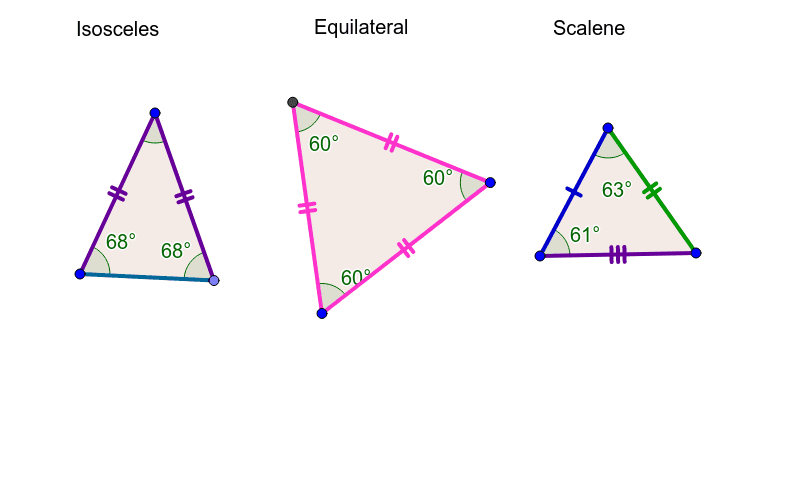
U3: Scalene Triangle V Equilateral V Isoceles

Scalene: All different side lengths and different angle measures

Equilateral: All angles are congruent, all side lengths are congruent

• also considered a isoceles because it has “at least” two congruent angles

Isoceles: “at least” two angles are congruent, opposite angles and sides are congruent (has a base angles, and vertex angles)

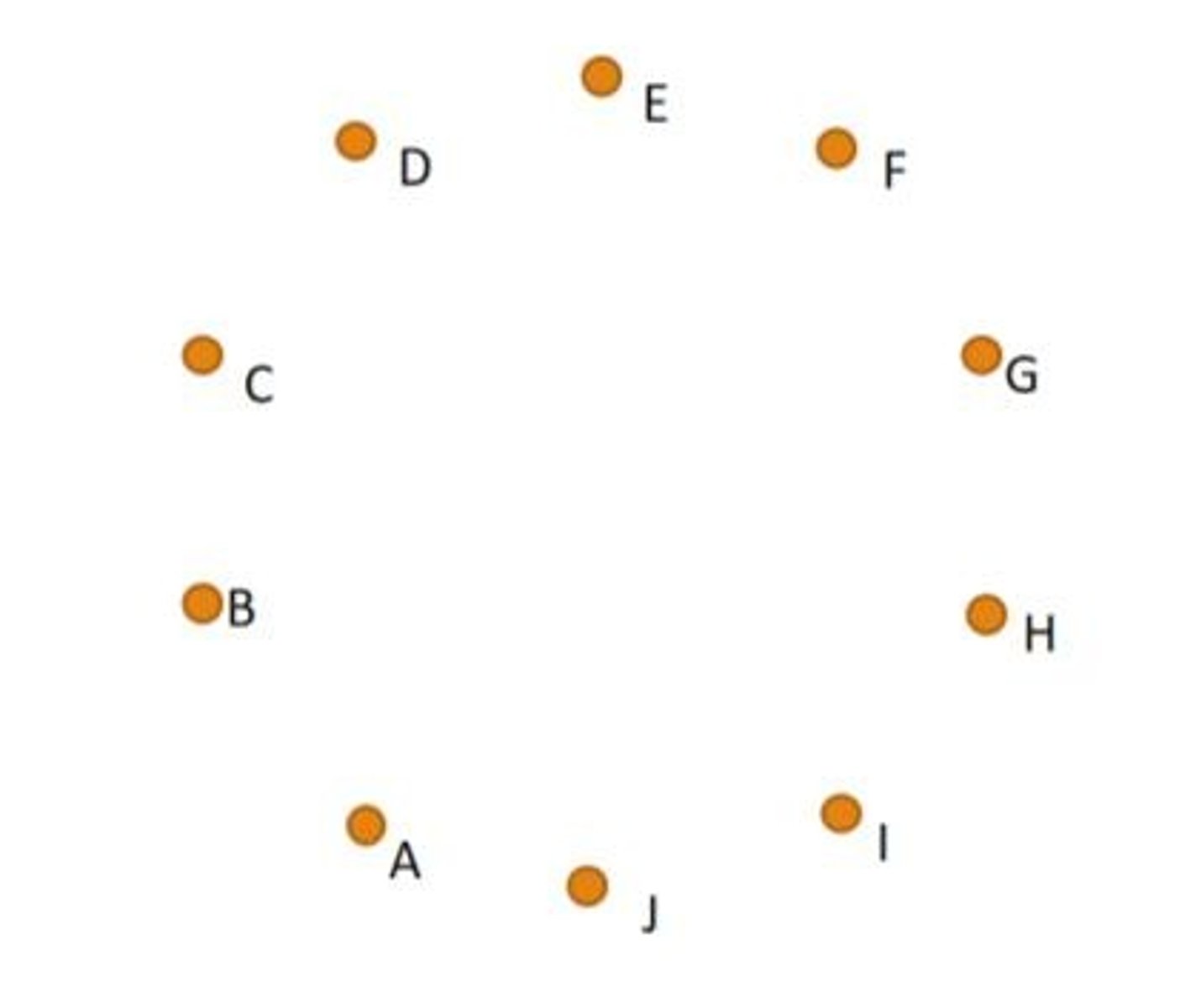
U3: What would be the formula used to solve the handshake problem? Why?

(n(n-1))/2 OR n minus 1 times n over 2

-Divided by 2 to account for double counting

-n(n-1) to represent the number of handshakes each person shakes time the number of people in total

U3: In a star, e+d+a+b+c= ________

180

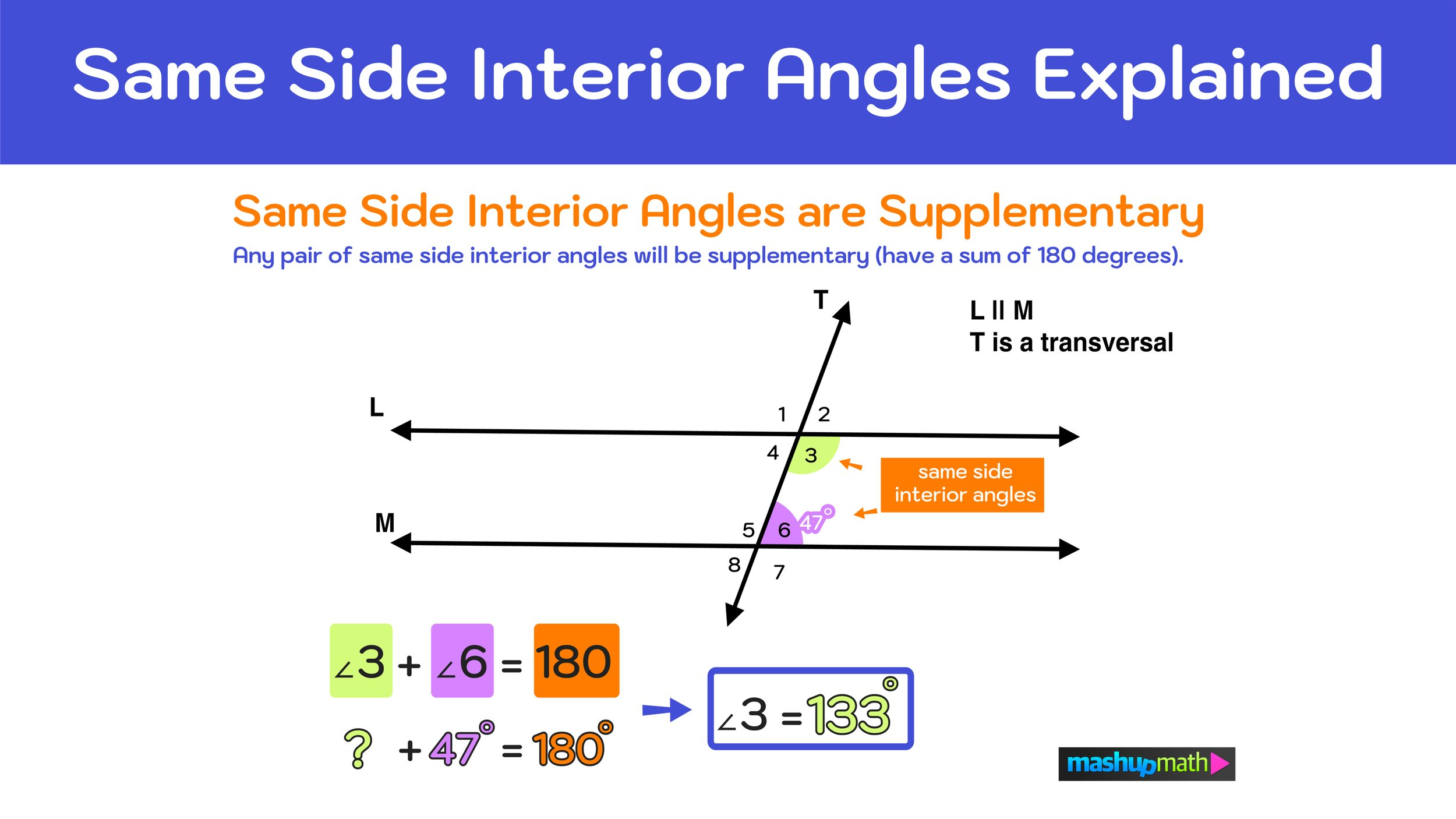
U3:Same side interior angle theorem

If two parallel lines are cut by a transversal, then same-side interior angles are supplementary.

U3: Reflex Angle

an angle that is greater than 180

U3: Define symmetric property, transitive property, and reflexive property

Symmetric= a=b b=c

Transitive = a=b b=c a=c

Reflexive = a=a

U3: Corresponding Angles Postulate

If a transversal intersects two parallel lines, then corresponding angles are congruent.

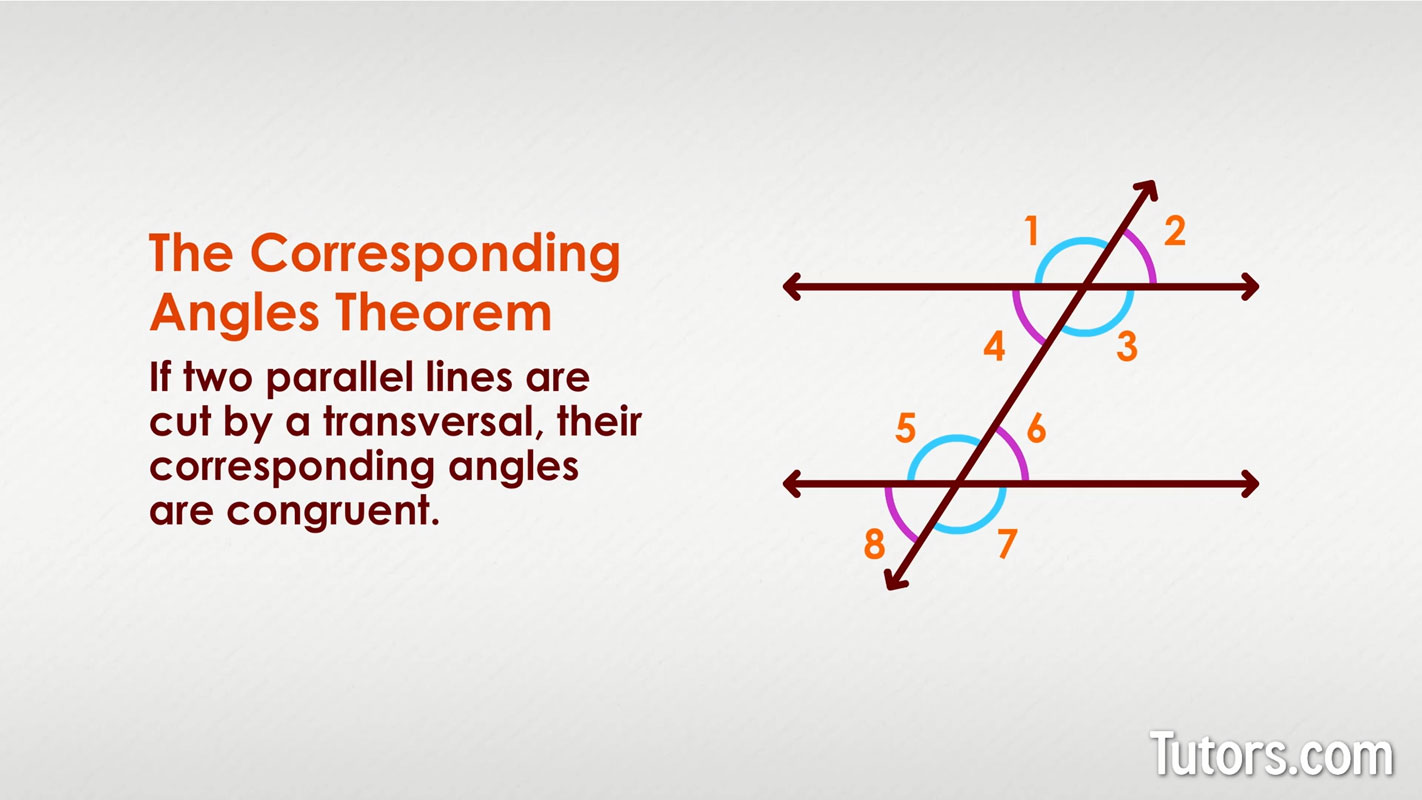
U3: Alternate angles theorem

If a transversal intersects two parallel lines, then alternate interior angles are congruent.

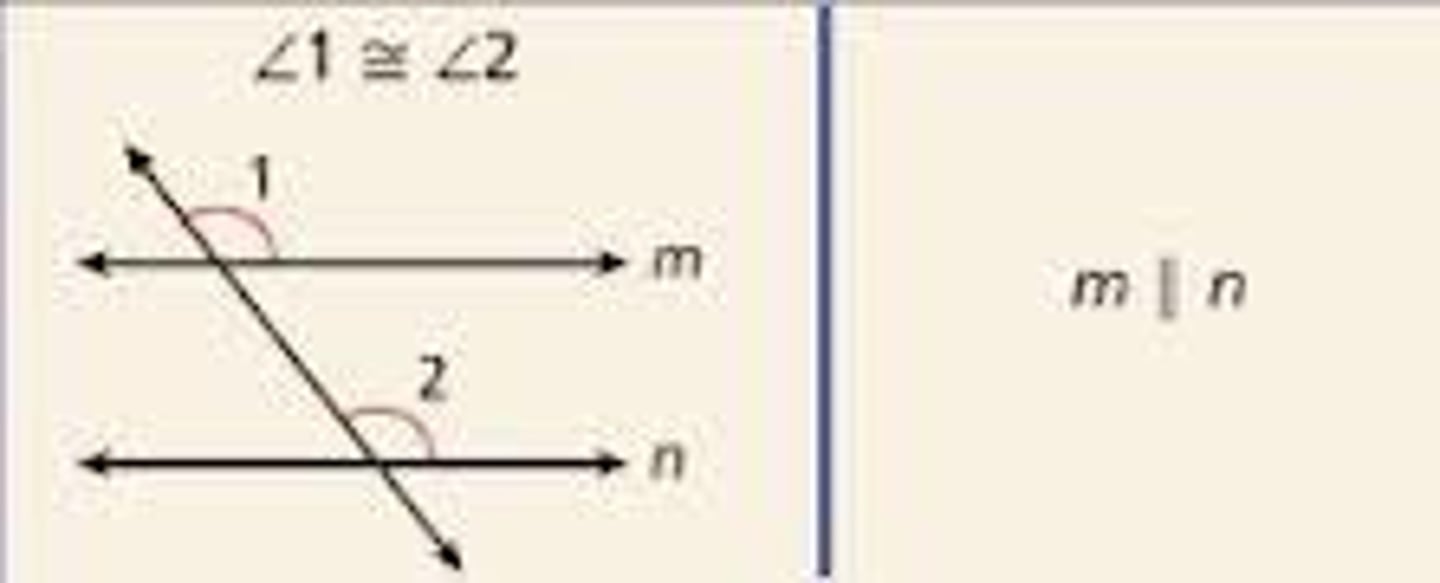
U3: Corresponding angles converse postulate

If two lines are cut by a transversal so that corresponding angles are congruent, then the lines are parallel.

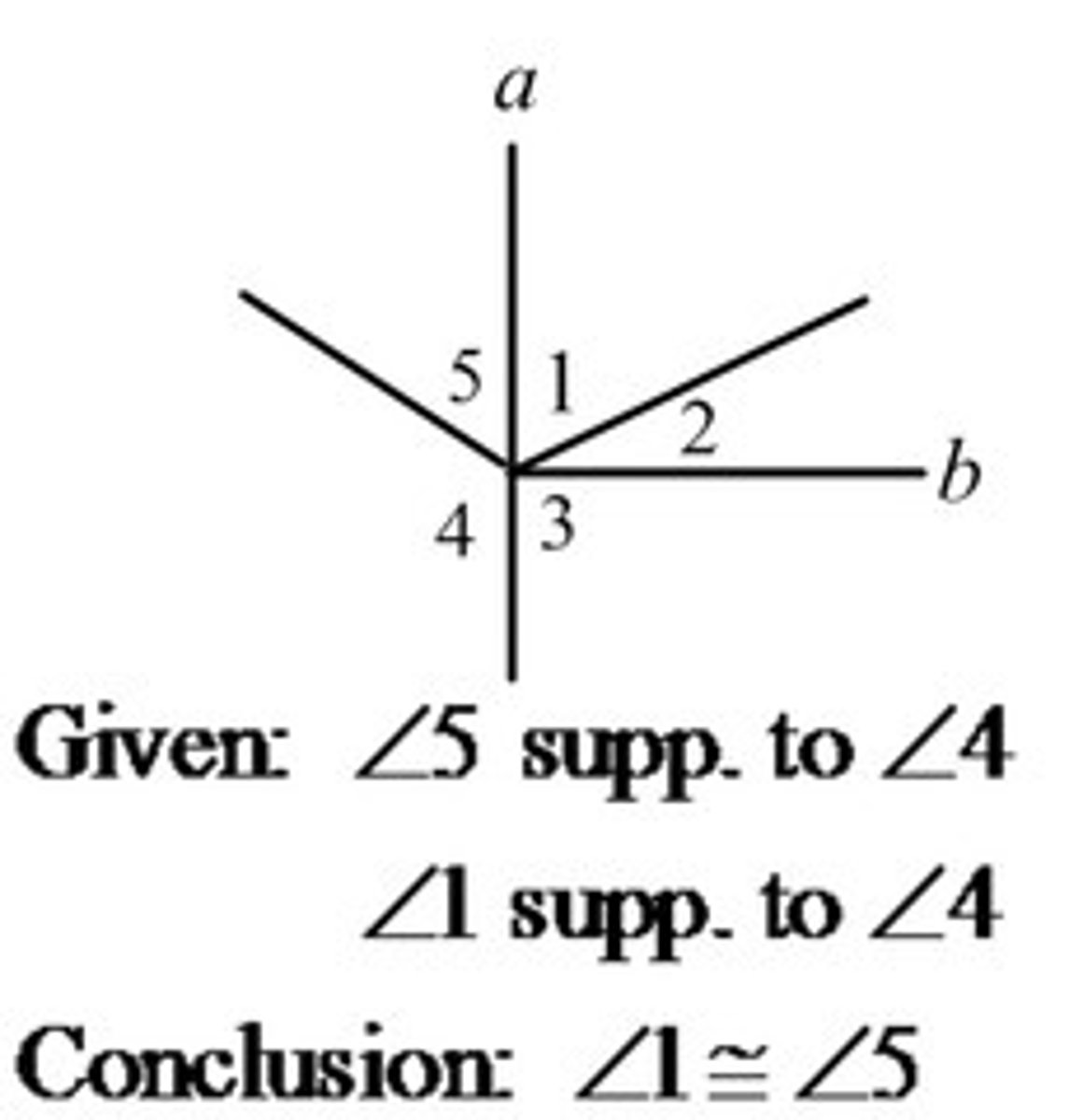
U3:Congruent Supplement Theorem

If two angles are supplementary to the same angle, then they are congruent

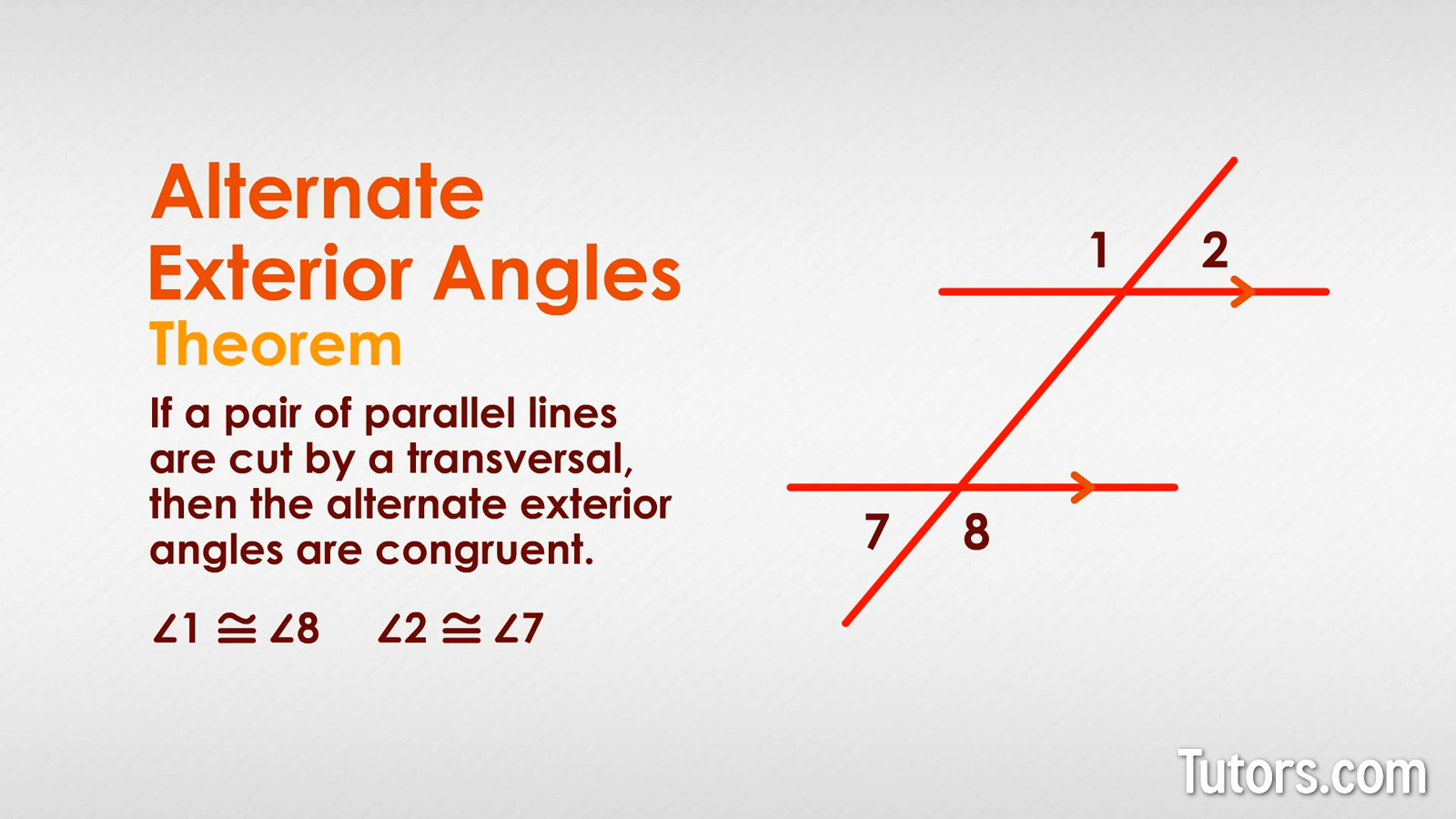
U3: Alternate interior angles converse thorem

If two lines are cut by a transversal so that alternate interior angles are congruent, then the lines are parallel

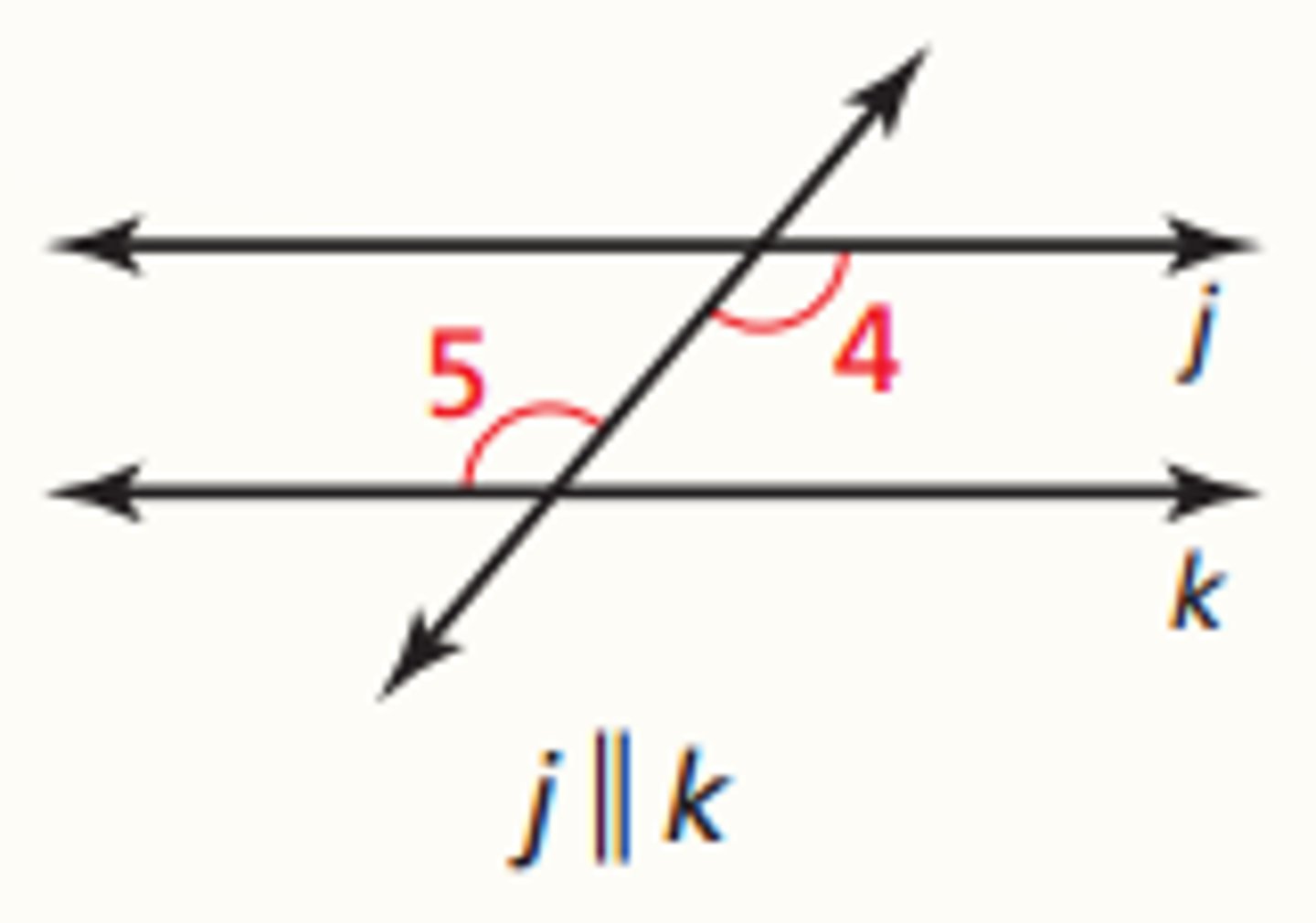
U3:Consecutive interior angles converse theorem

If two lines are cut by a transversal so the consecutive interior angles are supplementary, then the lines are parallel.

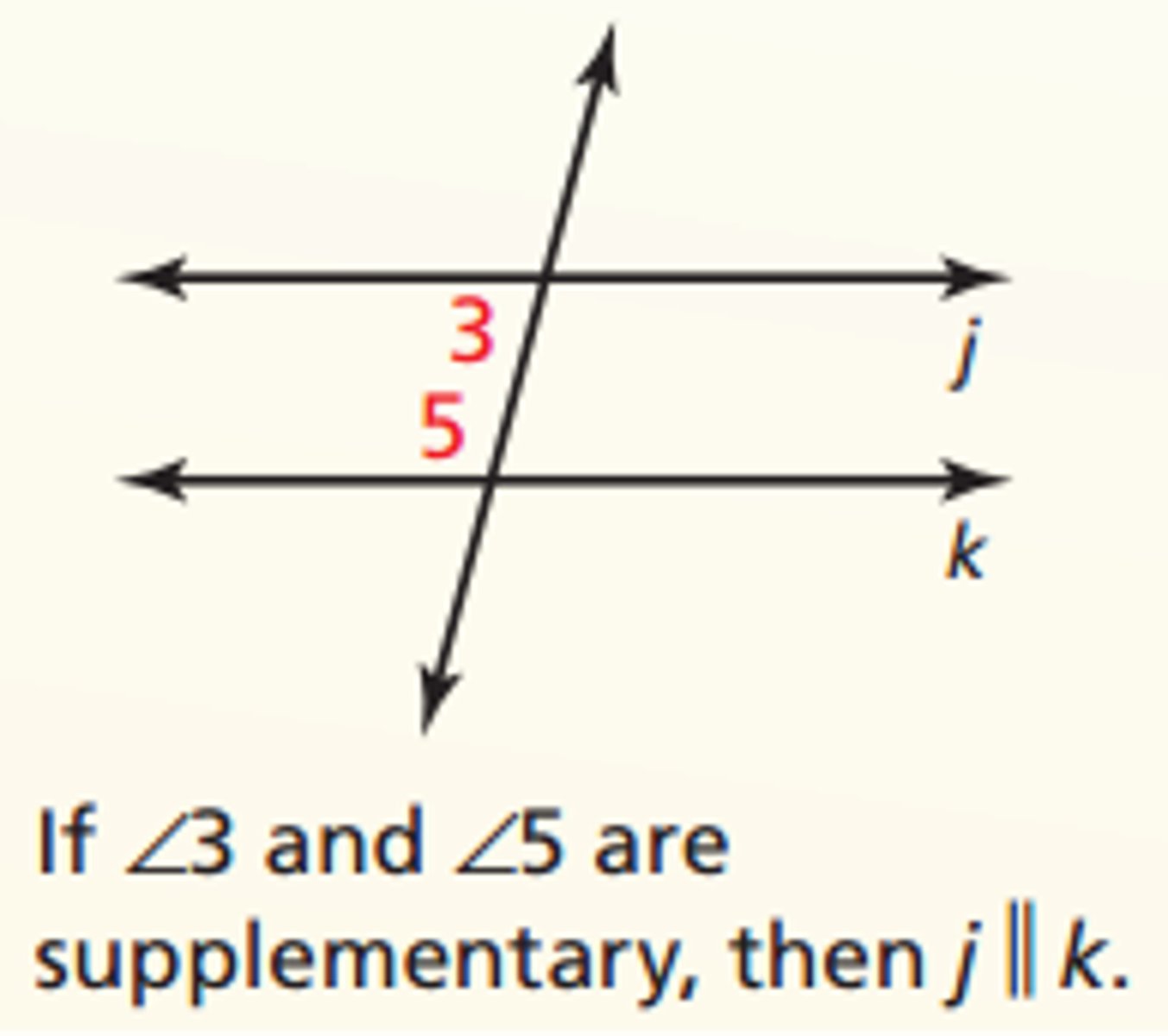
U3: Angle Bisector definition

a ray that divides an angle into two congruent adjacent angles

• EQUIDISTANT from RAYS (not endpoints!!)

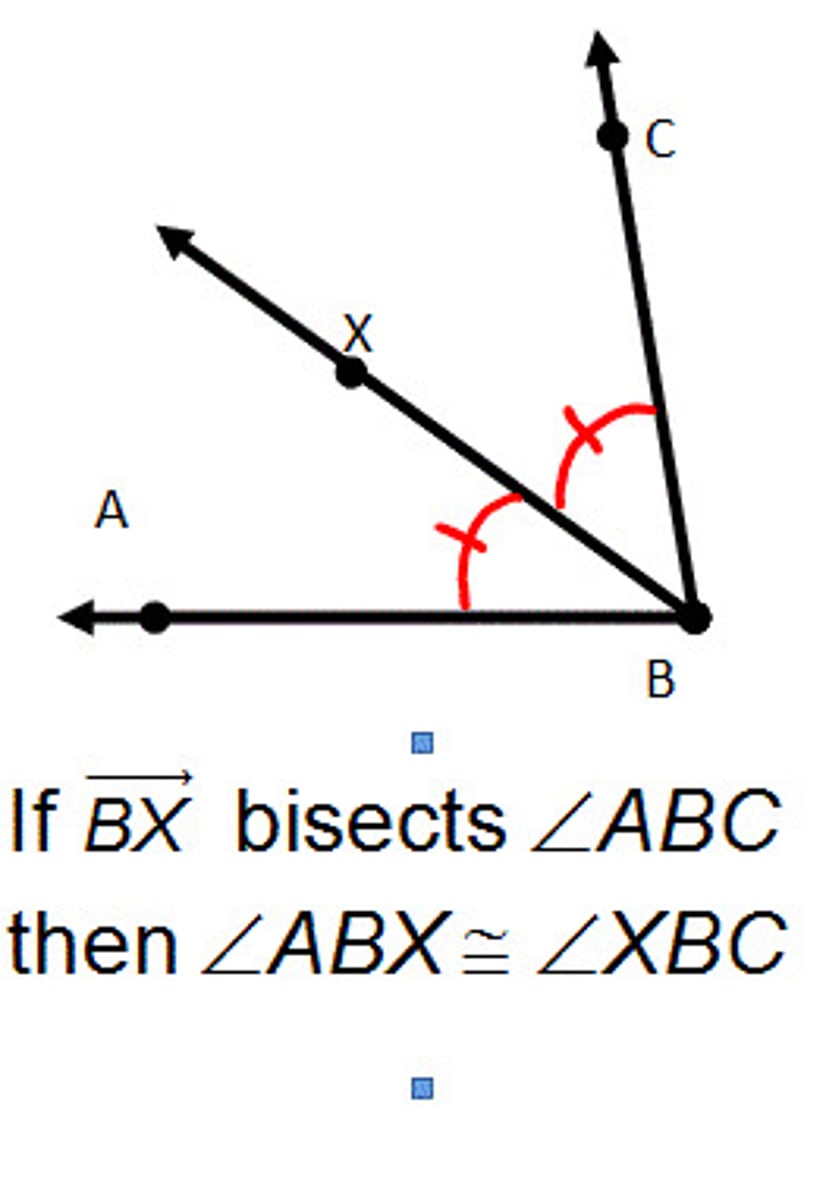
U3: Are corresponding angles always congruent?

NO! Only if the two lines are parallel (corresponding angles postulate)

—> MUST BE stated/marked in the problem/diagram

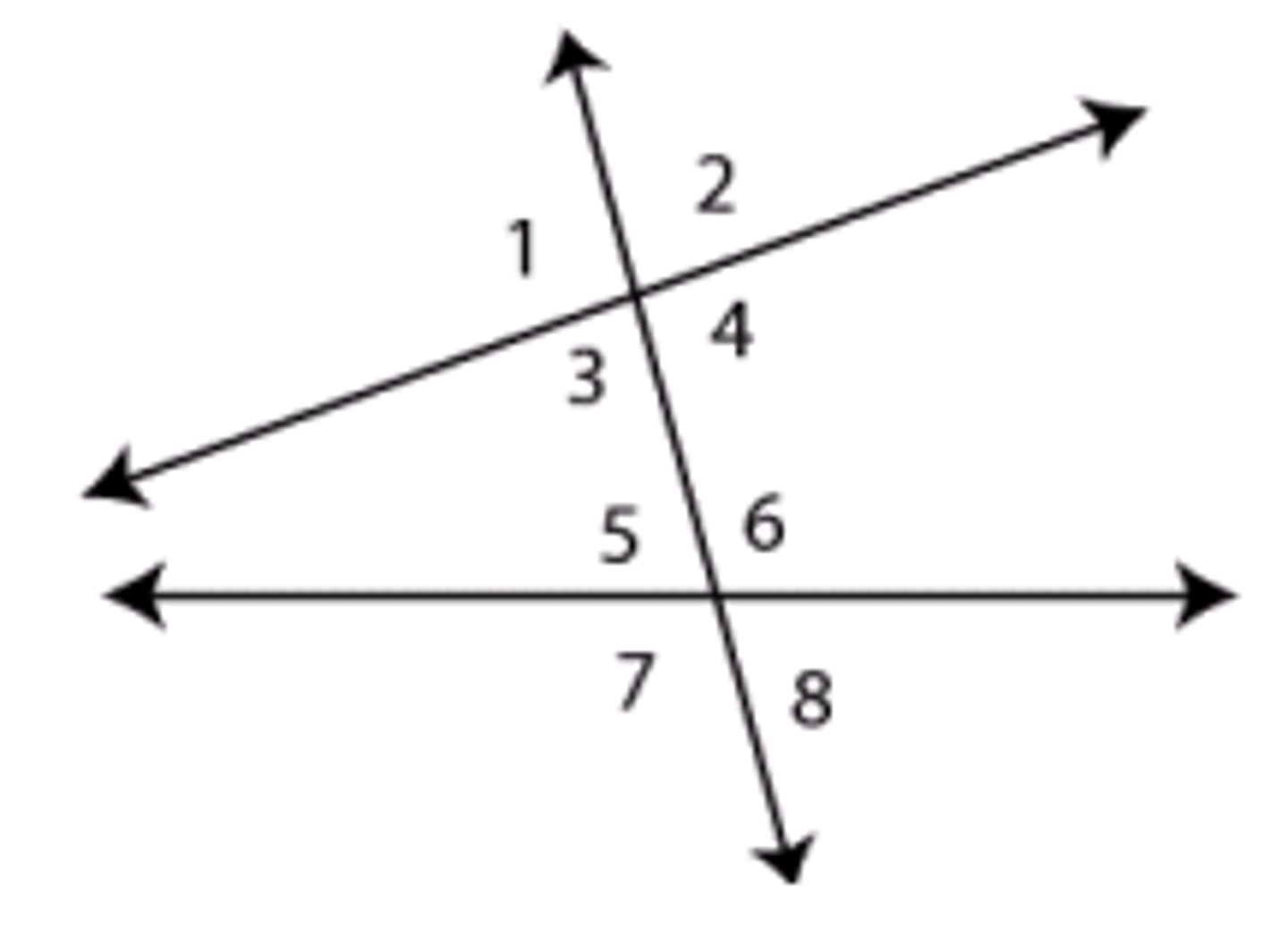
U3:If a transversal intersects 2 parallel lines

_______ angles are ________. ( hint: there are three)

Corresponding angles are congruent

Alternate interior angles are supplementary

Same side interior angles are congruent

REMEMBER: THIS ONLY APPLIES TO PARALLEL LINES LOOK FOR THE ARROWS

U3: What equation do we use to find the number of diagonals in a n sided polygon? How many diagonals per vertex? (Also: what is a diagonal)

(n(n-3))/n

n-3 diagonals per vertex

Diagonal: a straight line segment that connects two non-adjacent vertices (corners) of the polygon

*”n” = reprsents the sides of the polygon

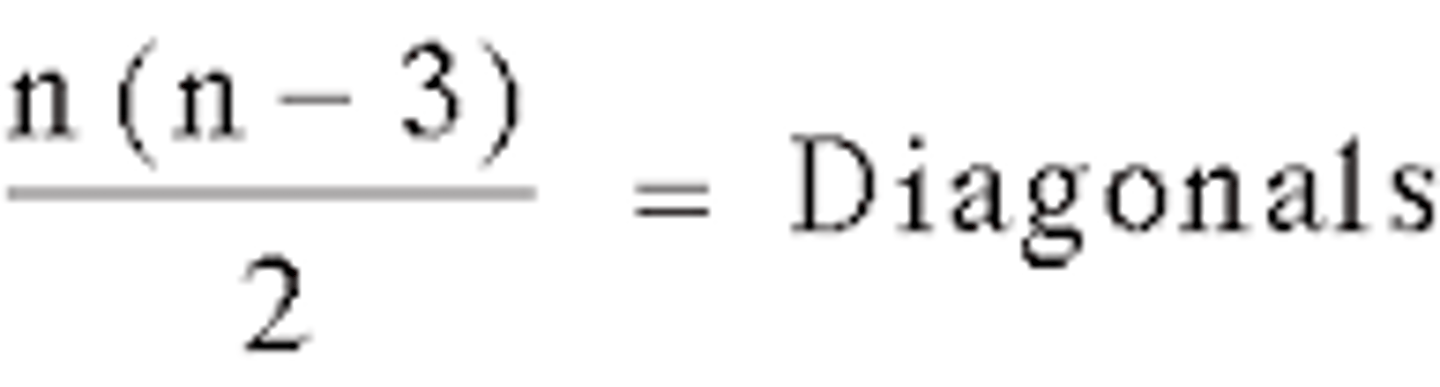
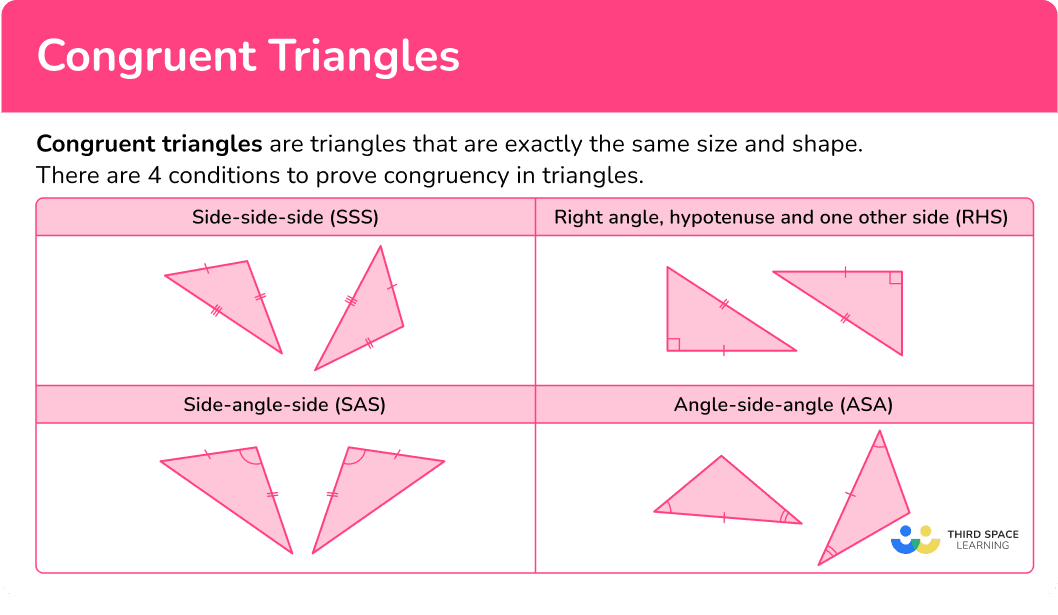
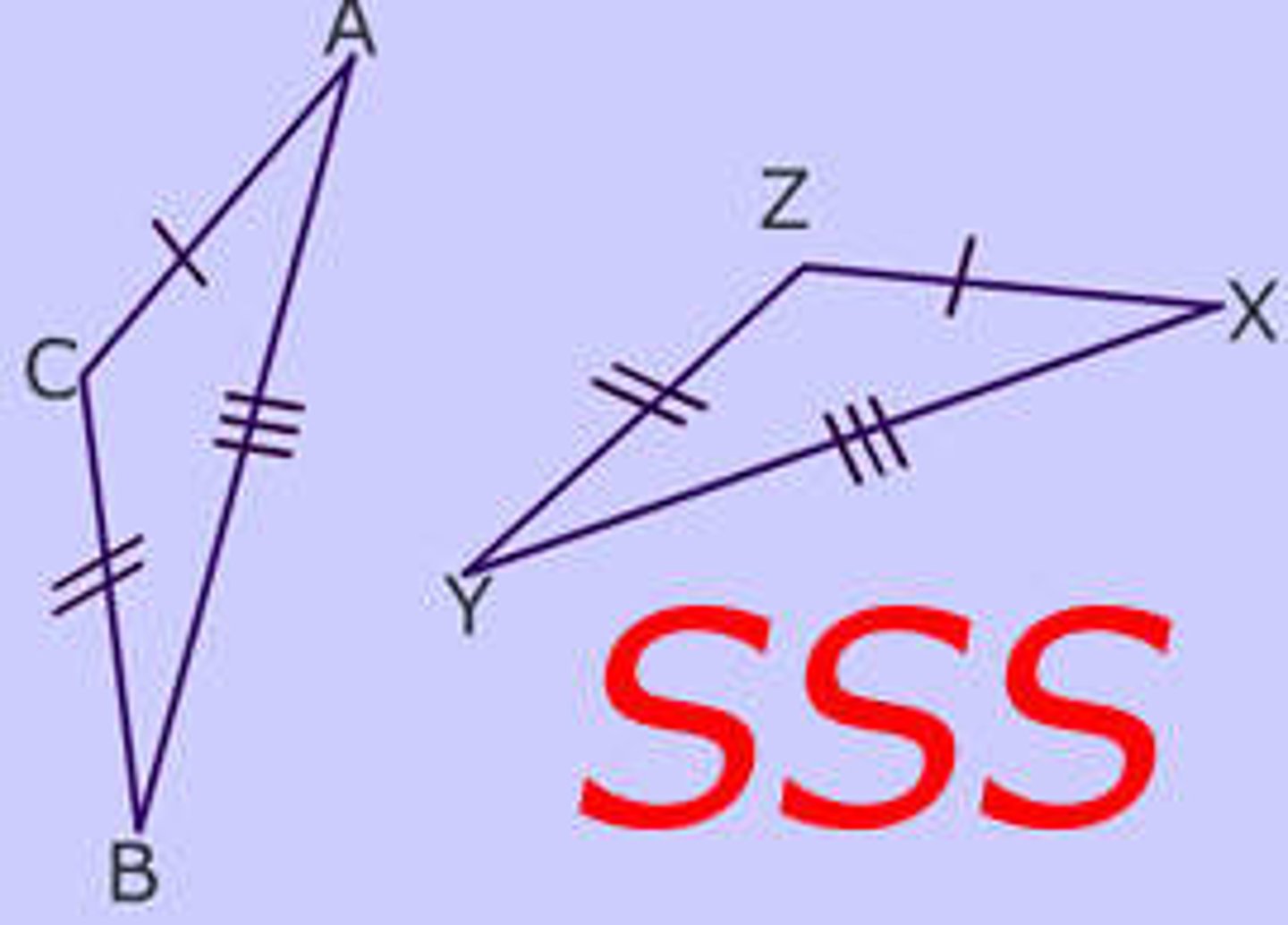
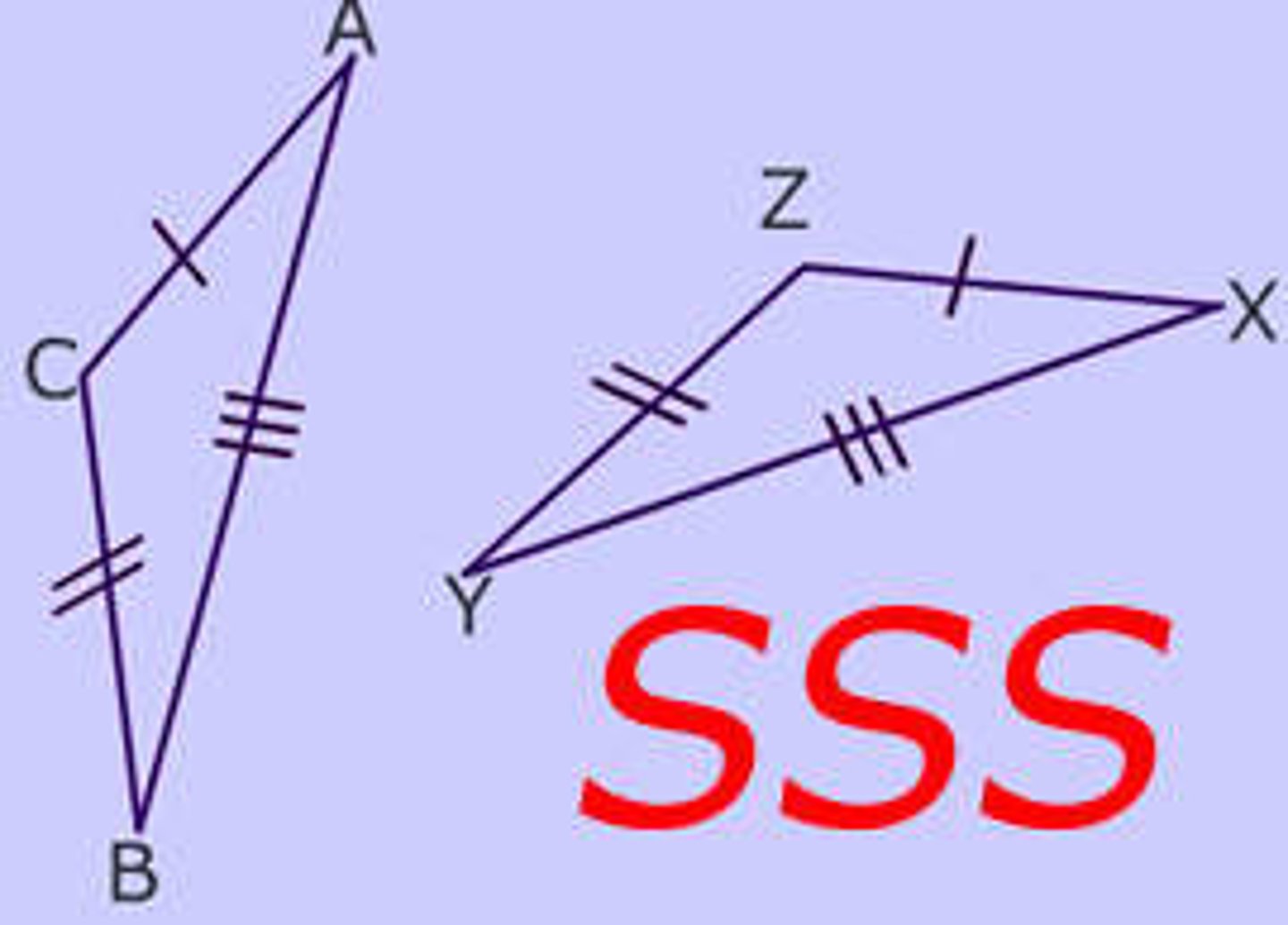
U3:SSS Postulate (Side-Side-Side)

If 3 sides of one triangle are ≅ to 3 sides of another triangle, then the triangles are ≅.

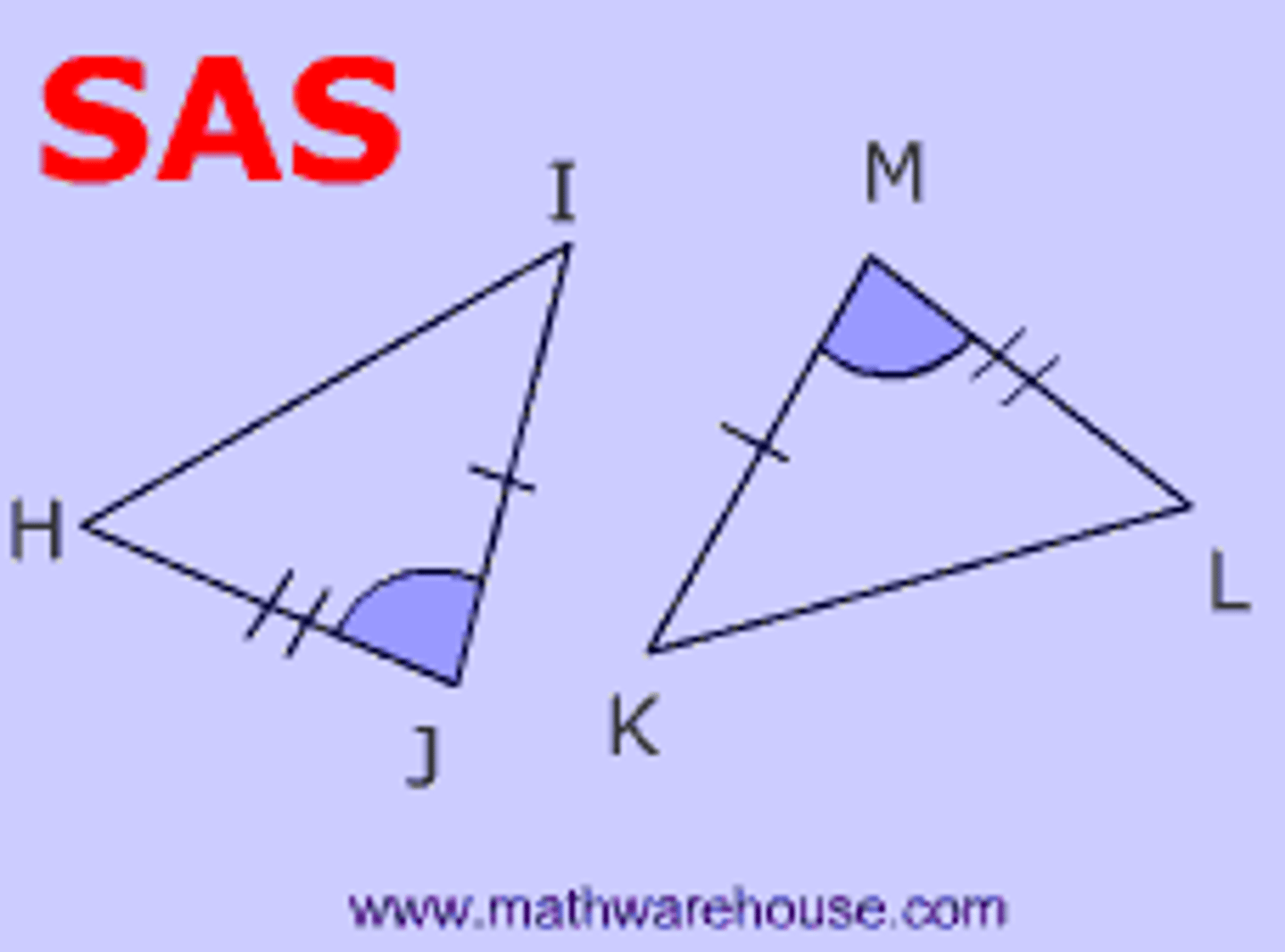
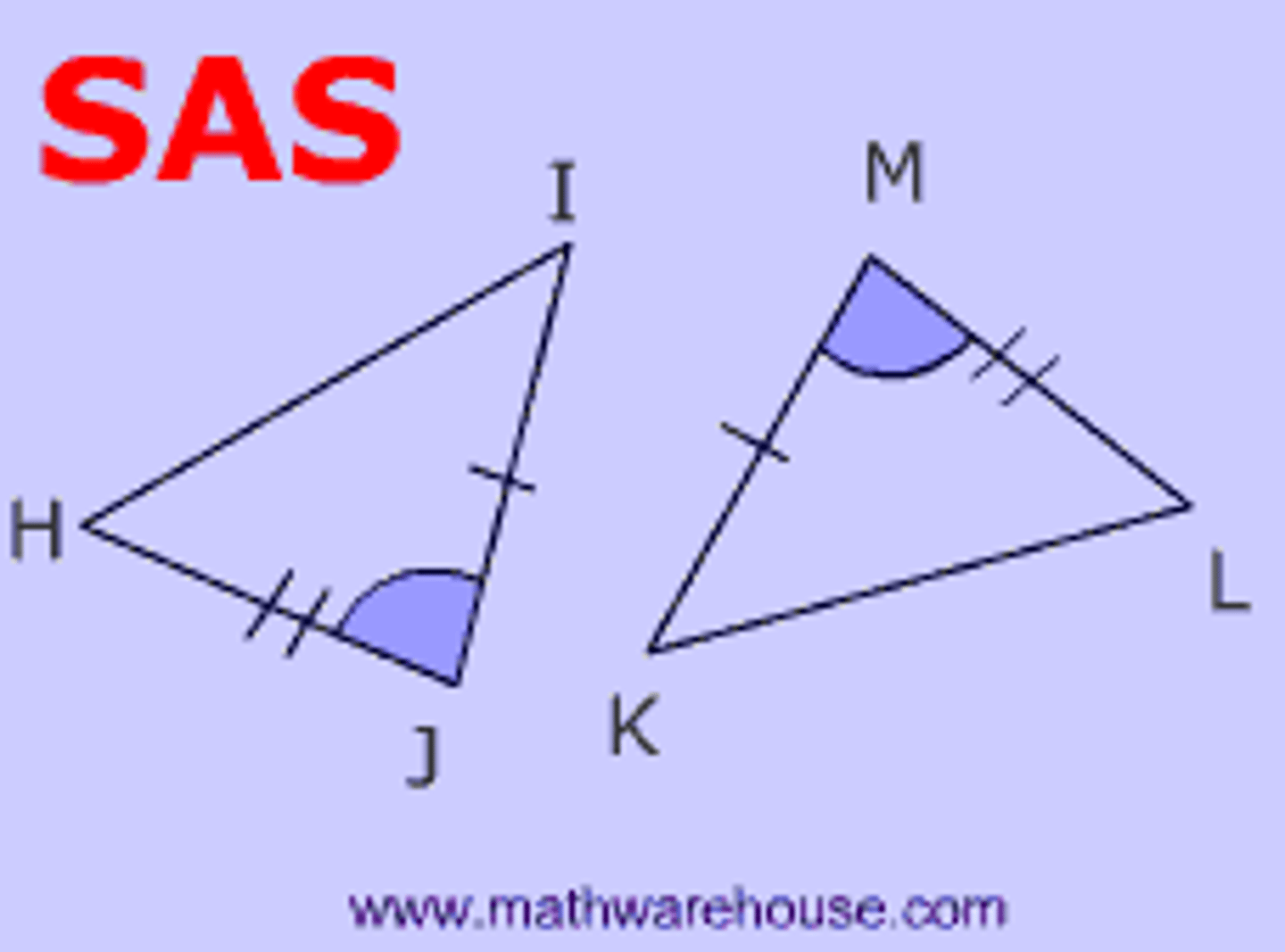
U3: SAS Postulate (Side-Angle-Side)

If 2 sides and the included angle of one triangle are congruent to 2 sides and the included angle of another triangle, then the triangles are congruent

*Included angle: Angle in between

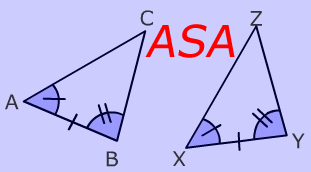
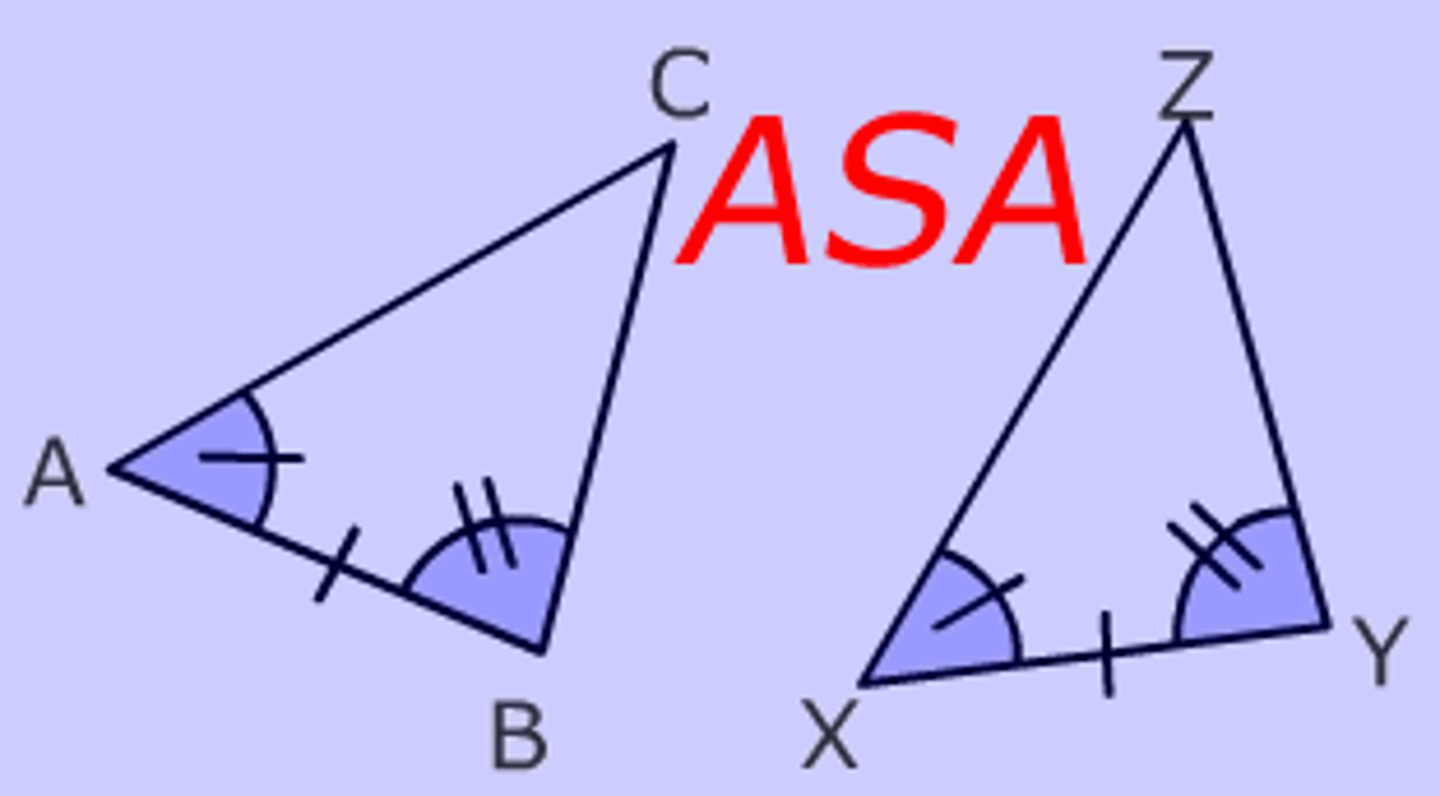
U3: ASA Postulate (Angle-Side-Angle)

If 2 angles and the included side of one triangle are congruent to 2 angles and the included side of another triangle, then the triangles are congruent.

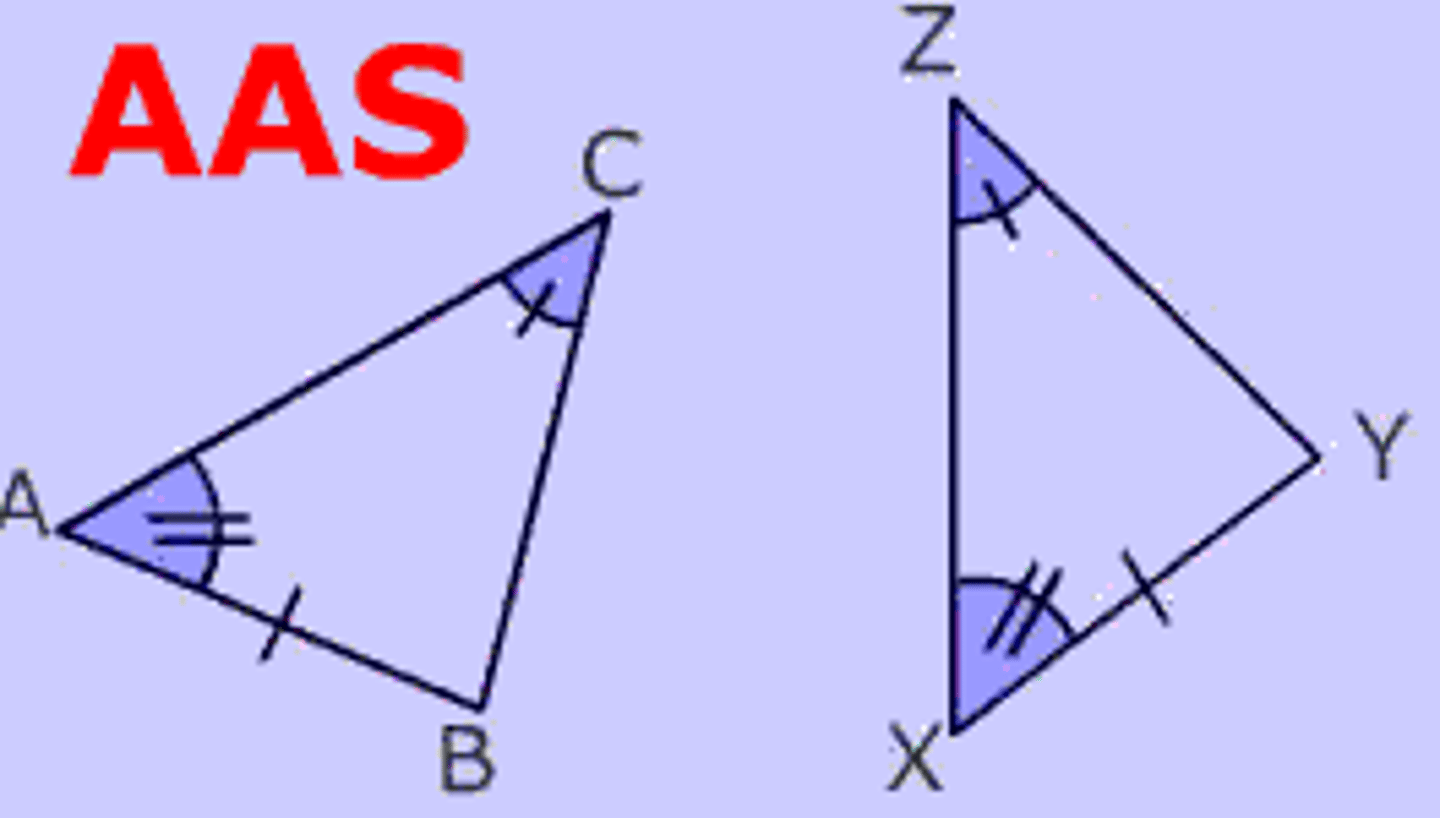
U3: AAS Postulate (Angle-Angle-Side)

If two angles and a side (THAT IS NOT INCLUDED) are congruent to two angles and a side (THAT IS NOT INCLUDED) of another triangle, the triangles are congruent.

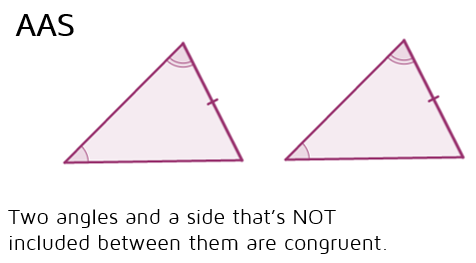
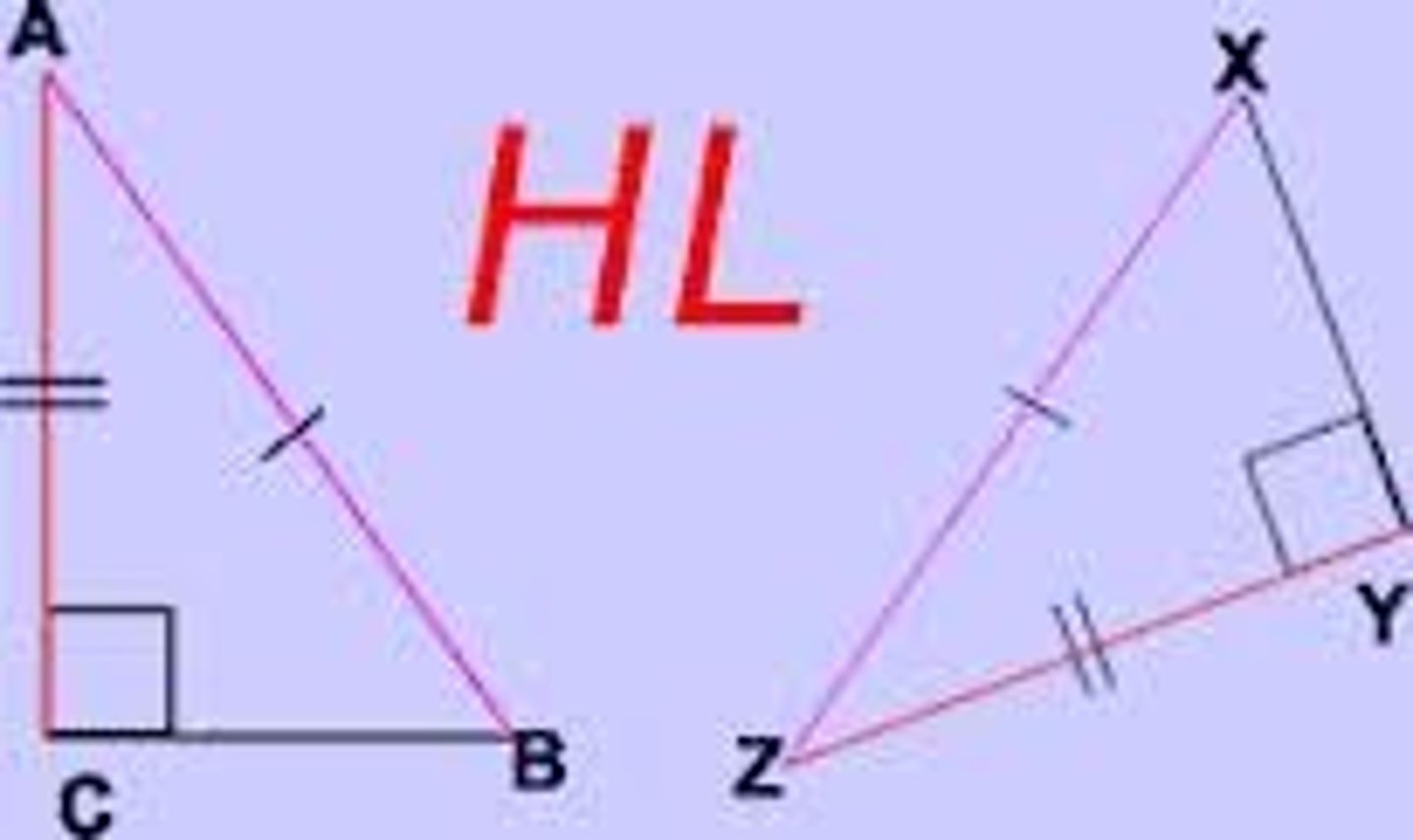
U3: HL Postulate (Hypotenuse-Leg)

If the hypotenus and one leg of a right triangle are congruent to the hypotenuse and leg of another right triangle the triangles are congruent.

• MUST prove both triangles are right trinalges before using this

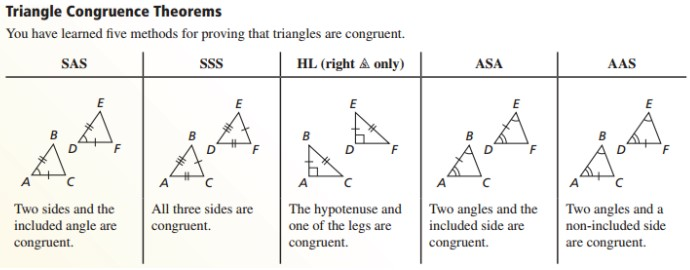
U3: What congruence postulates can you use to prove triangles are congruent?

SAS, SSS, HL, ASA, AAS

NEVER ASS

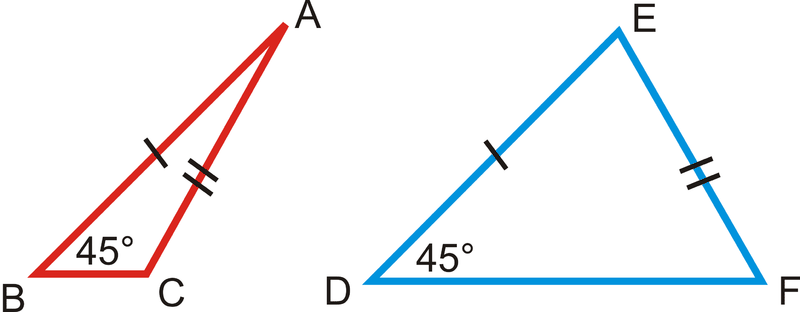
U3: Does ASS work as a congruence postulate?

U4/5: Side-Side-Side (SSS) Postulate

If 3 pairs of correspondjng sides are congruent, theb the triabgles are congruent.

U4/5: Side-Angle-Side (SAS) Postulate

If 2 sides and the included angle of one triangle are congruent to those parts of another triangle, then the 2 triangles are congruent.

-*included angle= angle in between

U4/5: Without knowing all 6 parts of a triangle we can show 2 triangles are congruent using...

AAA, HL, AAS, ASA, SSS

U4/5: Triangle Writing

Corresponding vertices must be in the same order

U4/5: Angle-Side-Angle (ASA) Postulate

If two pairs of angles and the angle between them of one triangle are congruent to the same parts in another triangle, then the triangles are congruent.

U4/5: Angle-Angle-Side (AAS) Postulate

If two angles and a non included side of one triangle are congruent to the corresponding two angles and non insured side of another triangle, then the two triangles are congruent.

U4/5: Hypotenuse-Leg (HL) Theorem

If 2 triangles have a right angle, a congruent leg, and a congruent hypotenuse, then the 2 triangles are congruent.

—> you MUST show the triangles are right in order to use it

U4/5: CPCTC

Corresponding parts of congruent then triangles are congruent.

-parts = angles or sides

—> only used for parts not triangles

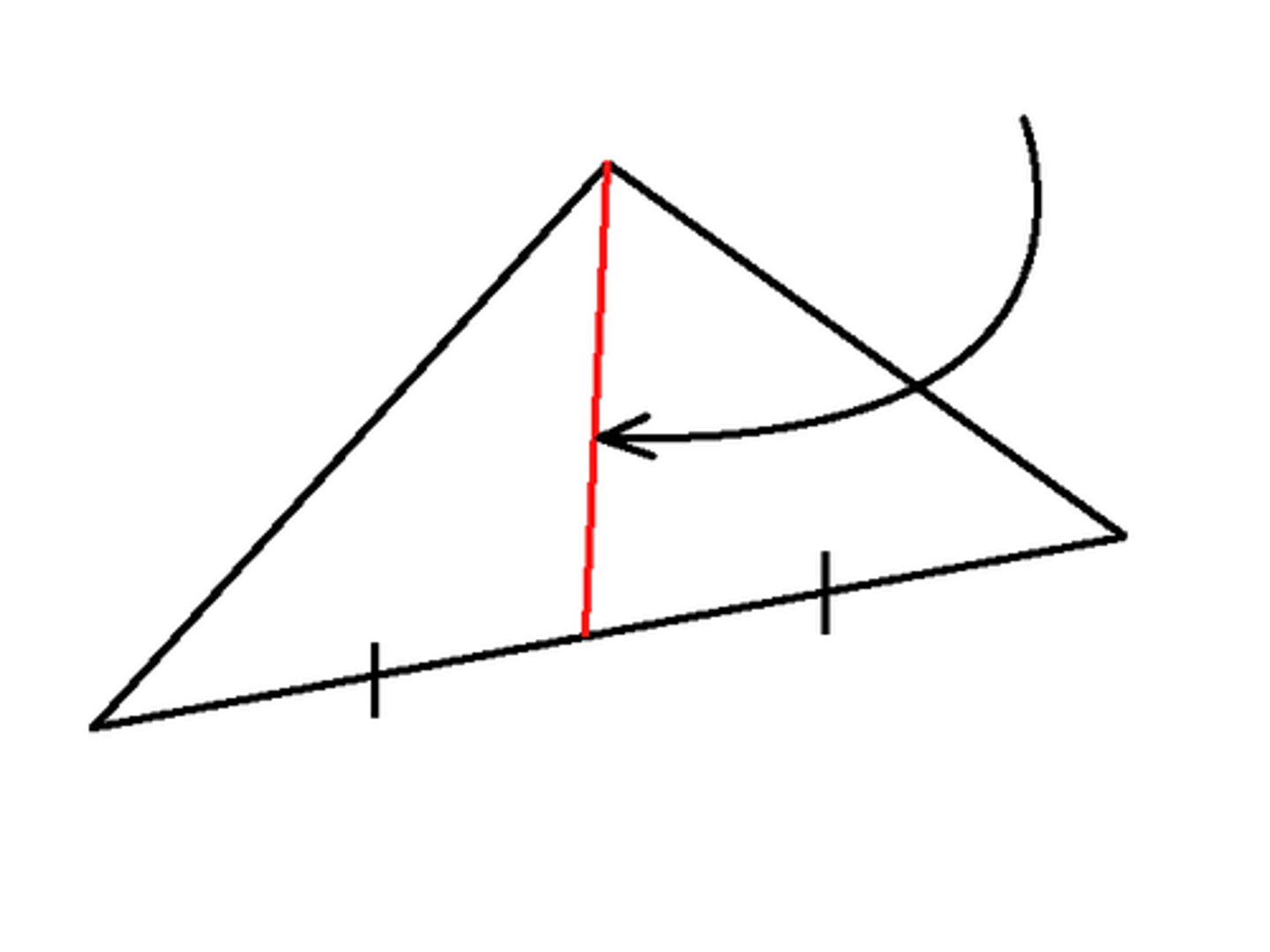
U4/5: Median

"Middle"

The median of a triangle is a segment from one vertex to the opposite midpoint.

U4/5: Formula for the area of a triangle

(height x base)/2

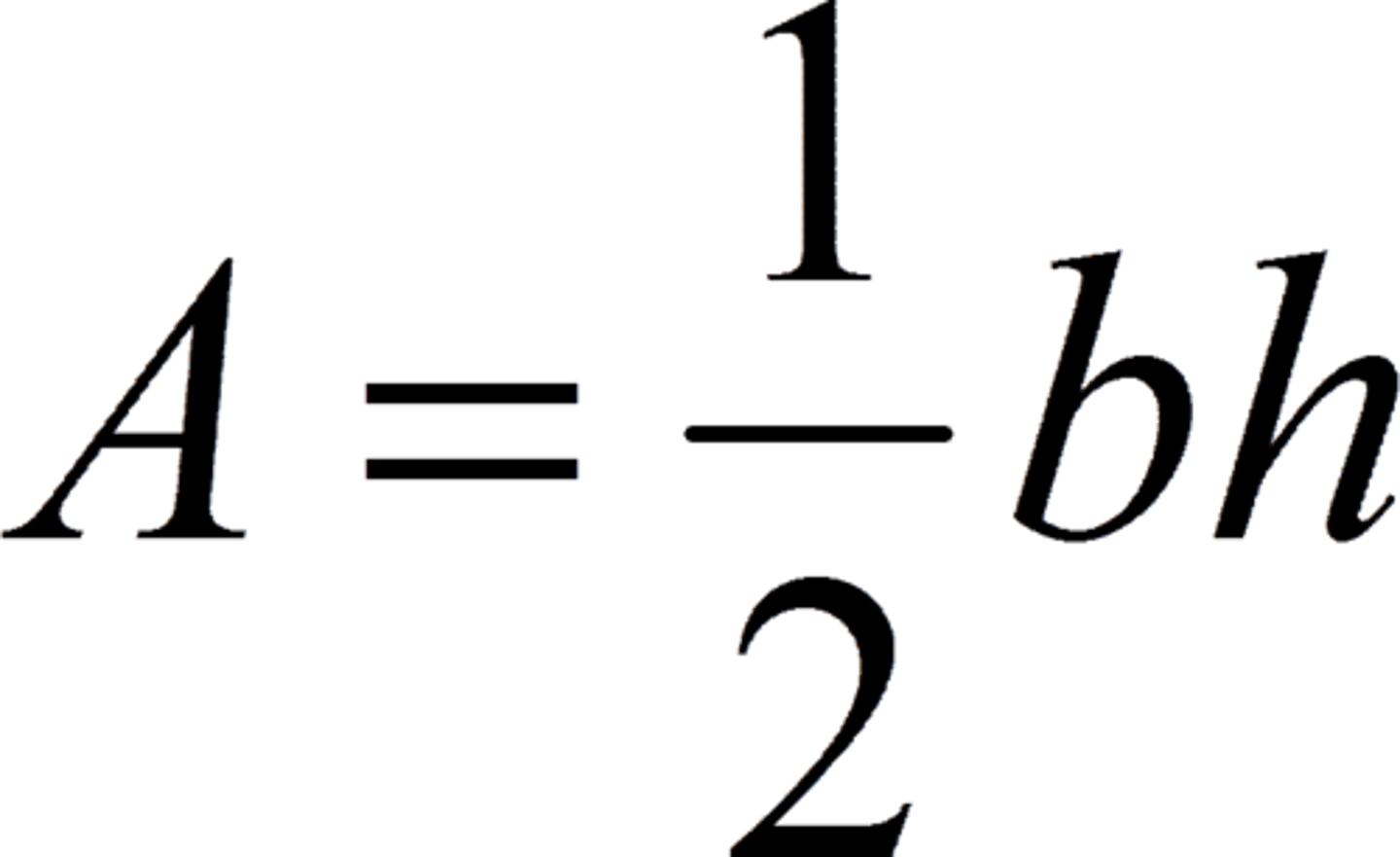
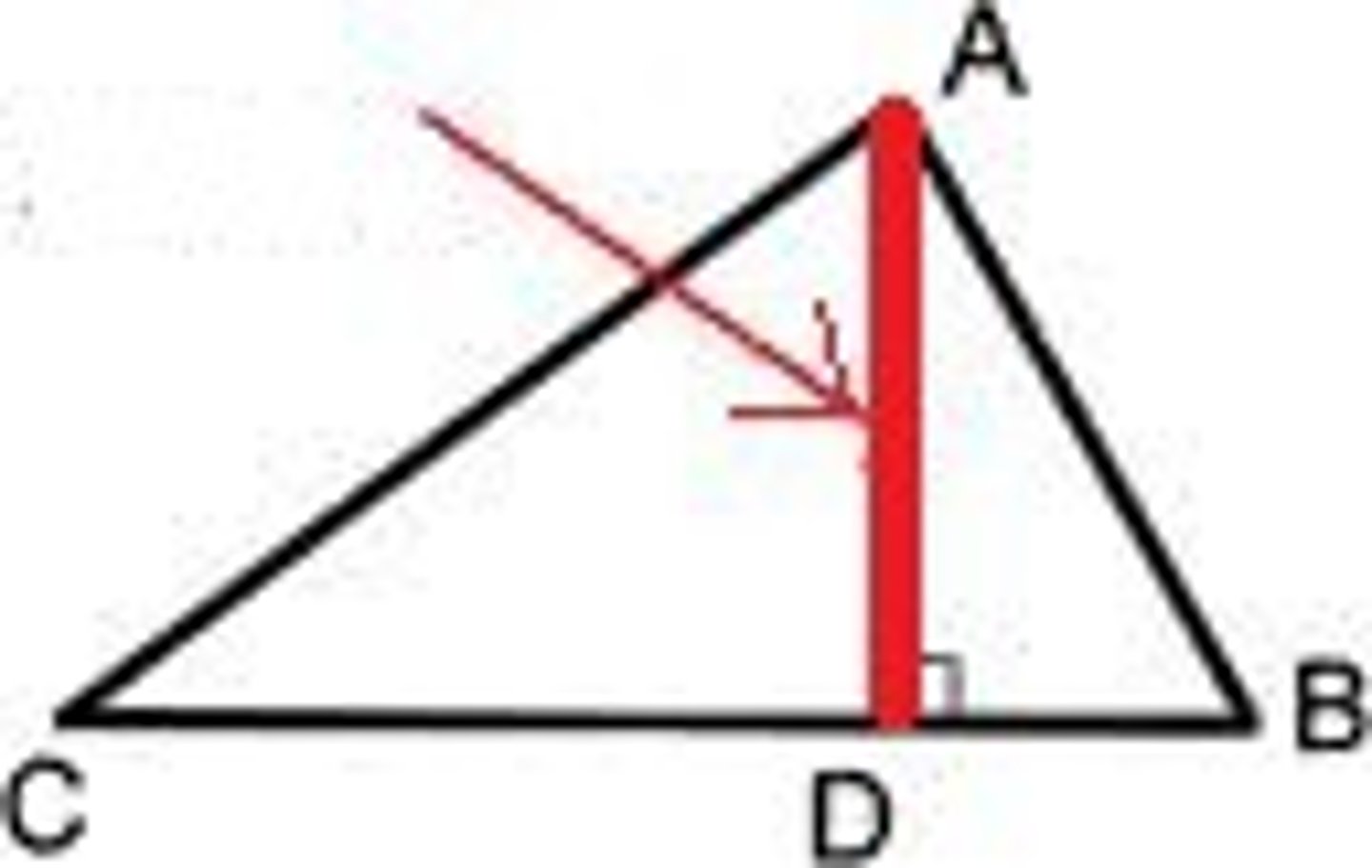
U4/5: Altitude

Height of something (triangle)

-height is always perpendicular to the base

-obtuse triangle = height is outside

-acute triangle= height inside

U4/5: Isoceles Triangle Theorem

If 2 sides of a triangle are congruent then the 2 opposite/across angles are congruent

U4/5: Isosceles Triangle Theorem Converse

If 2 angles are congruent then the 2 opposite of a triangle are congruent

U4/5: Perpendicular Bisector Theorem

If a point lies on the perpendicular bisector of a segment, then it is equidistant from the 2 endpoints of the segment.

U4/5: Converse of perpendicular bisector

If a point is equidistant from 2 end points of a segment then it is a perpendicular bisector.

U4/5: Angle bisector theorem

If a point lies in the angle bisector of an angle then it is equidistant from the 2 rays of the angle.

U4/5: How to be add or subtract segements or angles without converting to measures first?

We can use the Addition/subtraction postulates (not converting to the "measure of" before adding/subtracting) This is a shortcut and it not TECHNICALLY right but it okay for the midterms, tests, and regents.

U4/5: For three segments to form a triangle...

each side length must be less than the sum of the other 2 sides, but we only need to check the longest side (2 sides need to add to more than the longest side)

U4/5: In triangles the longest side must be...

greater than the sum of the other 2 sides

|y-z| < x < y+x

(Assuming x is the largest, assuming x is the smallest)

U4/5: the smallest angle is opposite the ______________angle and the largest angle is opposite the _____________ angle.

The largest angle is opposite the longest side.

The smallest angle is opposite the smallest side.

(angle is smaller, side is smaller, angle is larger, the side it larger)

U4/5: What are the three a^2+b^2 equations? and for what triangles?

a^2+b^2 a= c^2 (right triangle)

a^2+b^2 > c^2 (actute triangle)

a^2+b^2 < c^2 (obtuse triangle)

U4/5: Is SSA enough to prove congruence? AAA?

No, multiple triangles can be made. (THINK: ASS)

No, AAA will create SIMMILAR triangles, NOT CONGRUENT TRIANGLES

U4/5: If two angles are congruent and supplementary they just both be ________ angles

Right

U4/5: How to do quadatic equations

Combine like terms, Make one side equal zero(quadratic), then factor and use zero product property

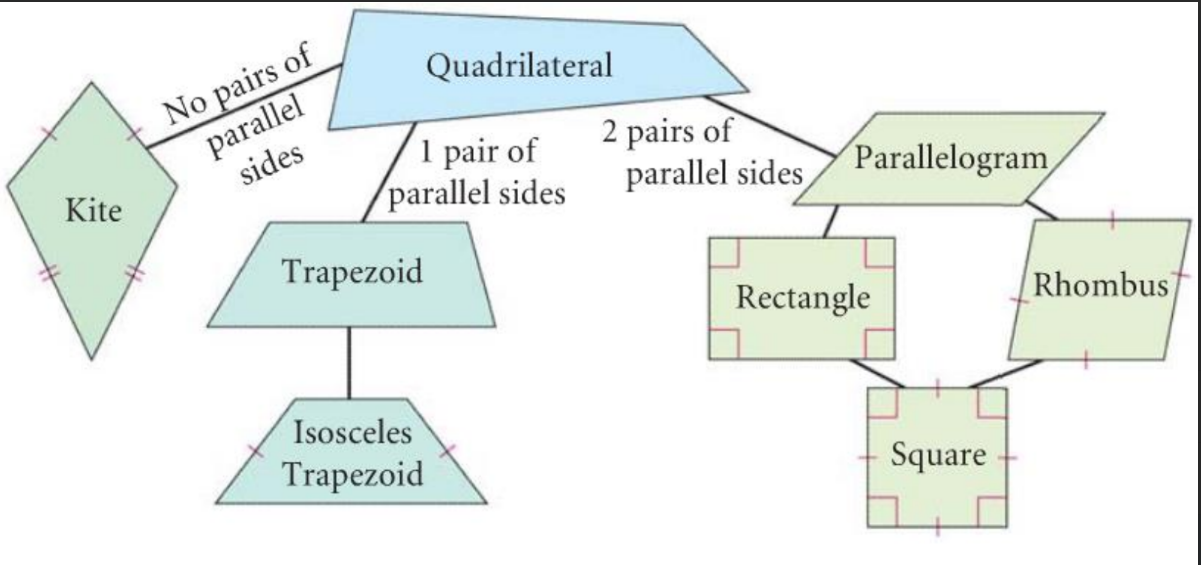
U6: Rectangles are also...

-parallelograms

-quadrilaterals

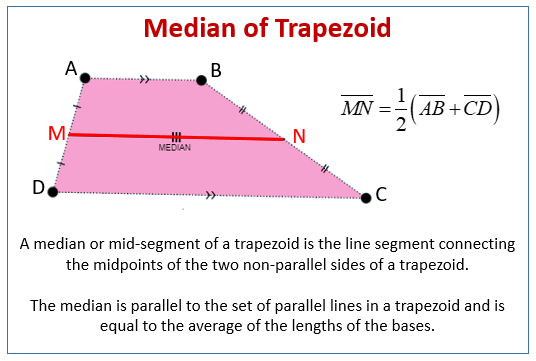
U6: Trapezoid median

Segment between the midpoint of the non parallel sides of a trapezoid

(Average of the lengths of the 2 bases) —> Also parallel to the bases

Median = (b1 + b2)/2

U6: If a parallelogram has congruent diagonals then its a ———-

If it has perpendicular diagonals it's a ———

If both it's a ——-

Rectangle

Rhombus or kite

Square

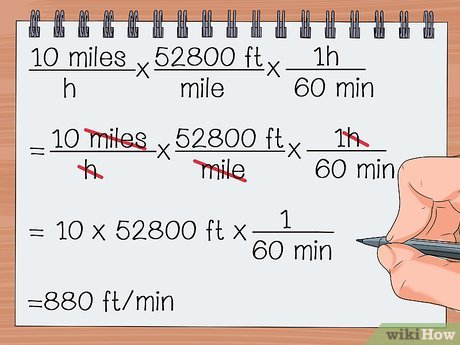
U6: Converting units

Multiple fractions till the units cancel out (top and bottom)

Multiply by fractions/units equivalent to 1

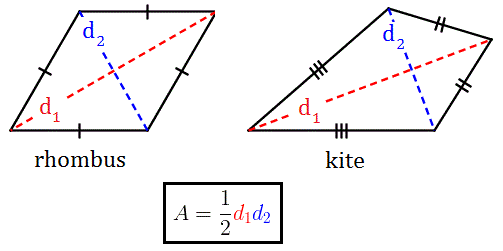
U6: Kite/Rhombus area formula

(D1xd2)/2 (splitting into triangles)

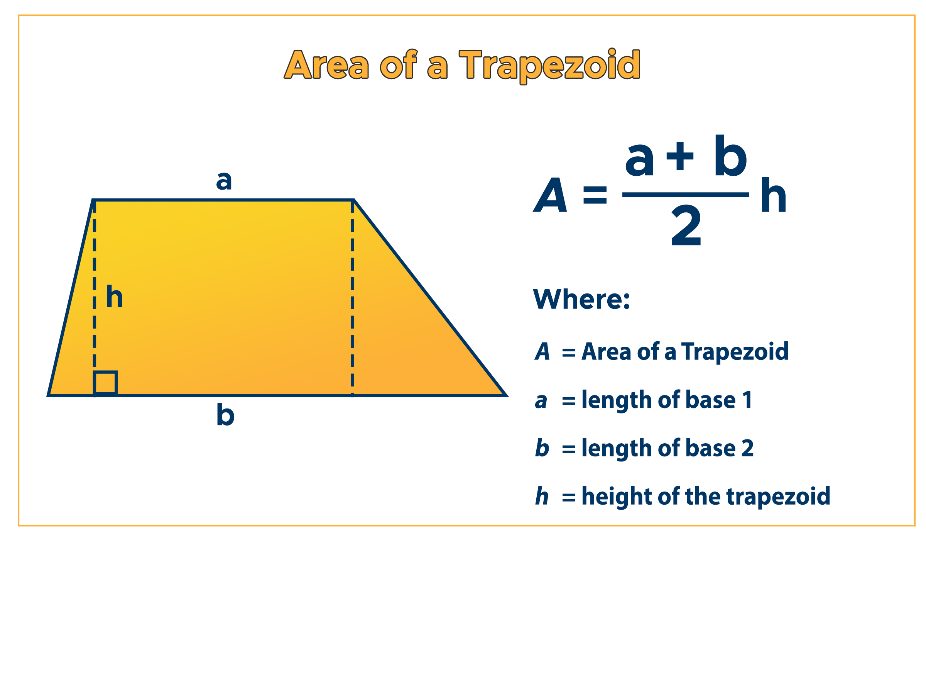
U6: Trapezoid area formula

(b1+b2)h/2

—> (two parallelograms)

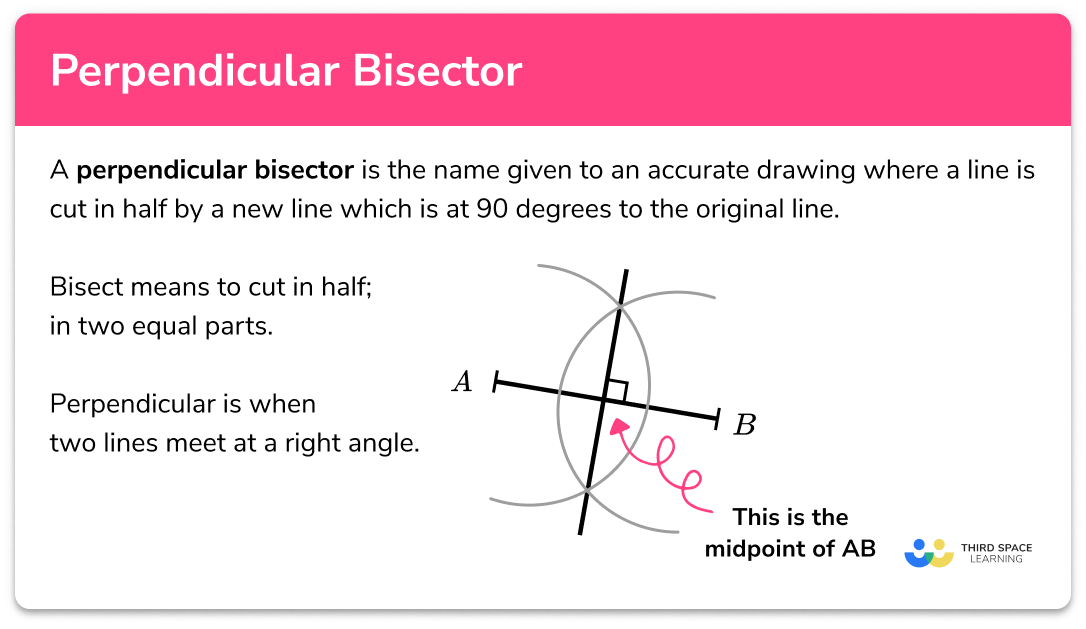
U6: Perpendicular Bisector

A line that bisects a segment (breaks into two congruent parts), and is perpendicular to the segment (forms right angles)

• Equidistant from endpoints.

• Perpendicular to base.

U6: If a parallelogram has congruent diagonals it is a _________

If a parallelogram has perpendicular diagonals it is a ________.

If it's both that it's a _________.

Rectangle, rhombus, square

U6: Congruent Supplements Theorem

If two angles are supplementary to the same angle (or to congruent angles), then they are congruent.

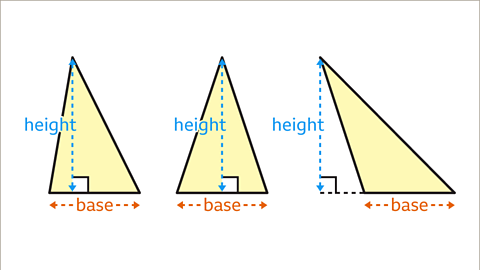
U6: How are base and height related on a triangle?

Base and height are perpendicular. Height is also called altitude

-base can be any side

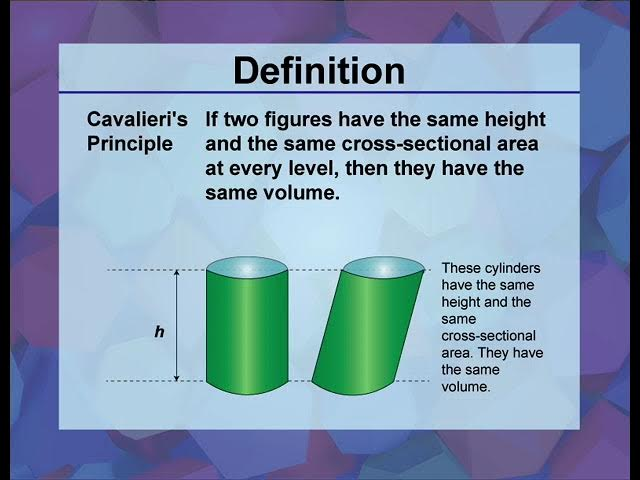
U6: Cavaliers principle

2 figures have the same area if they have the same height and width at every point along that height

U6: Rectangle (characteristics/how to prove)

Quadrilateral with 4 right angles

• Diagonals are congruent and bisect eachother

  • They are NOT perpendicular (exception = square)

• 4 right angles

• Parallelogram

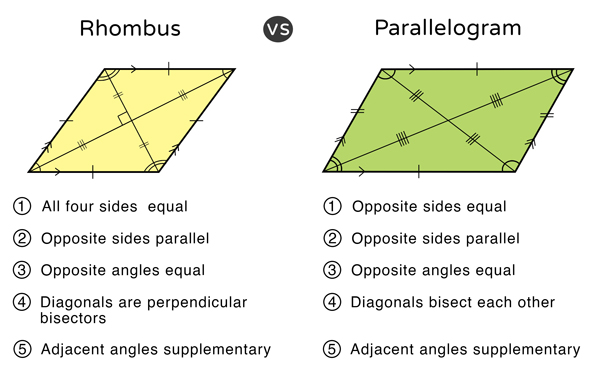
U6: Rhombus (characteristics/how to prove)

A quadrilateral with four congruent sides and 4 congruent angles

• 4 congruent sides

• 4 congruent angles

• Paralleogram

• Diagonals are perpendicular bisectors

  • Bisect eachother

  • Form right angles

  • NOT equal

U6: Trapezoid (characteristics/how to prove)

A quadrilateral with exactly one pair of parallel sides

• NOT a paralleogram (only one pair parallel)

  • Non parallel sides = legs, parallel sides = bases

  • the diagonals are generally not congruent and do not bisect each other

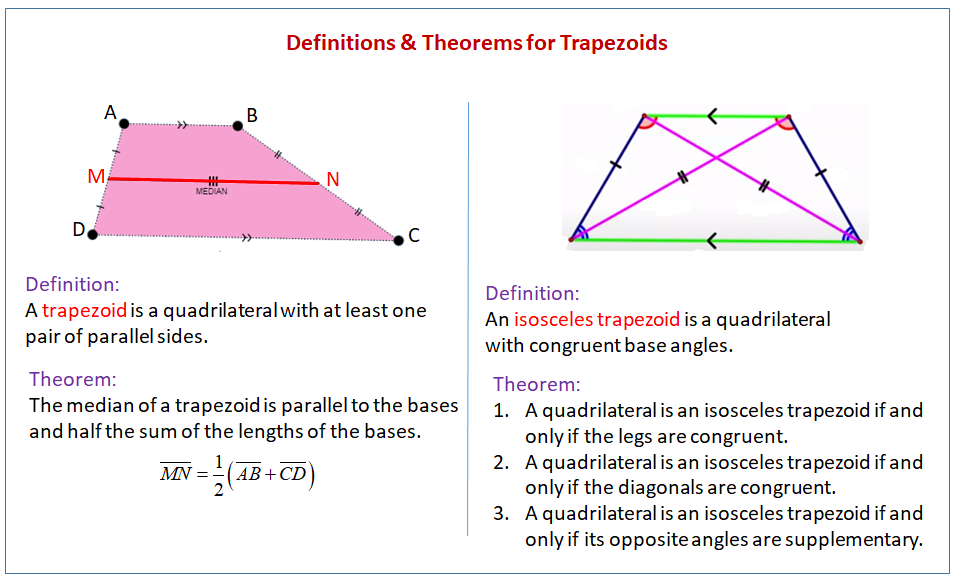
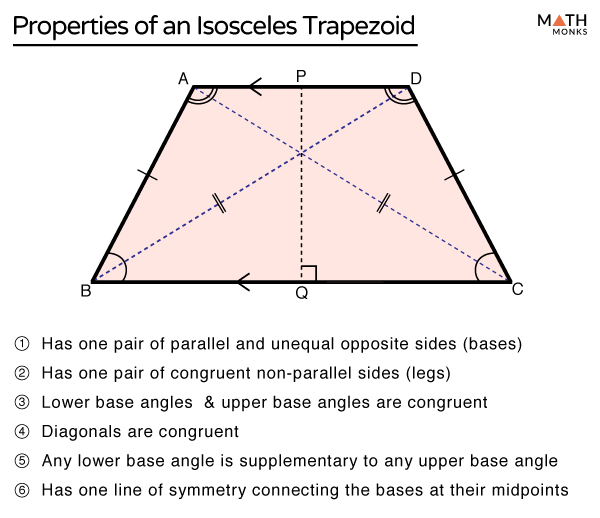
U6: Isosceles Trapezoid

An isosceles trapezoid is a trapezoid where the two non-parallel sides (legs) are equal in length. This also means that the base angles are congruent (equal in measure). 

• One pair of parallel and unequal opposite sides (bases

• One pair of congruent non parllel sides (legs

• Diagonals are congruent

  • Do not bisect eachother

• Any lower base angle is supplementary to any upper base angle

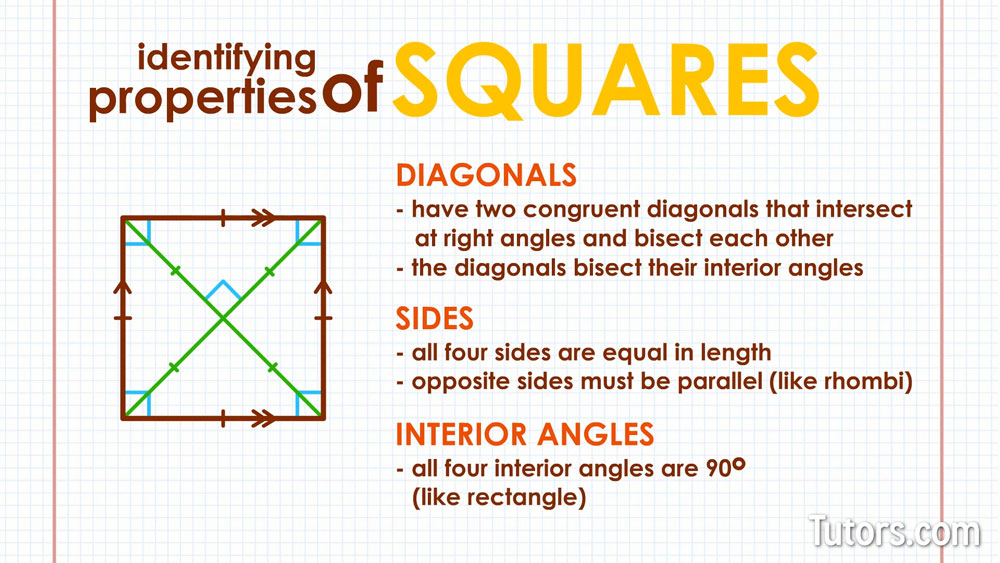
U6: Square

A quadrilateral with 4 congruent sides and 4 right angles

• is also (by definition) a rectangle and a rhombus

Characteristics:

• Four equal sides

• Four right angles

• Diagonals are equal in length:

• Diagonals are perpendicular bisectors

  • A square is a rhombus so it shares the same characteristics, diagonals are perpendicular bisectors

  Regular polygon: Because all sides and angles are equal, a square is a type of regular polygon. 

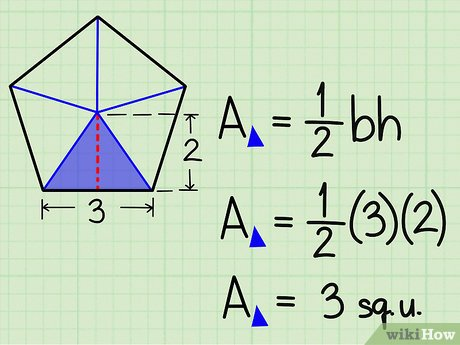
U6: Area of a regular pentagon

(Apothem x perimeter)/2

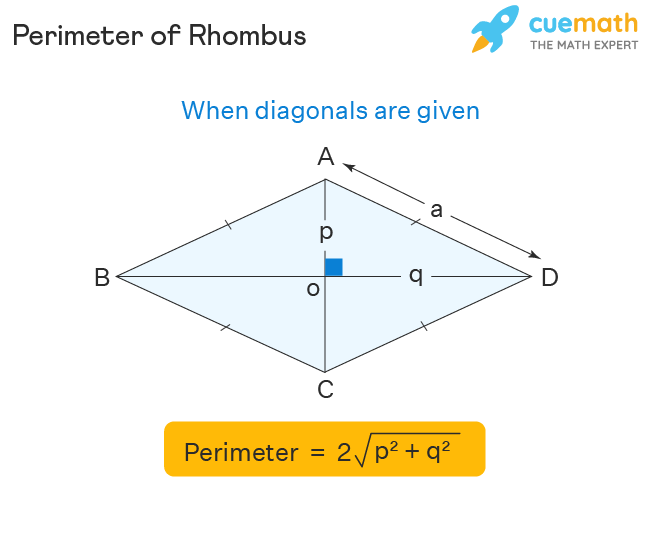
U6: Equation for the rhombus perimeter (in terms of diagonals)

2√p2+q2

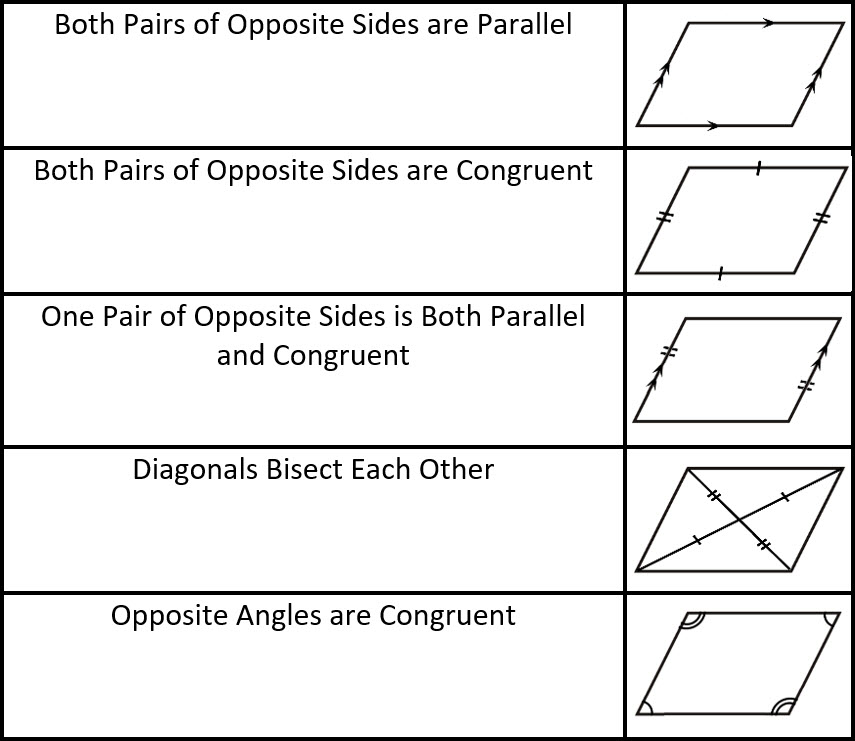
U6: Ways to prove a quadrilateral is a parallelogram

1) Prove both pairs of opposite sides are congruent:

2) Prove both pairs of opposite sides are parallel:

3) Prove one pair of opposite sides is both congruent and parallel:

4) Prove that the diagonals bisect each other:

5) Prove that opposite angles are congruent:

6) Prove consecutive angles are supplementary:

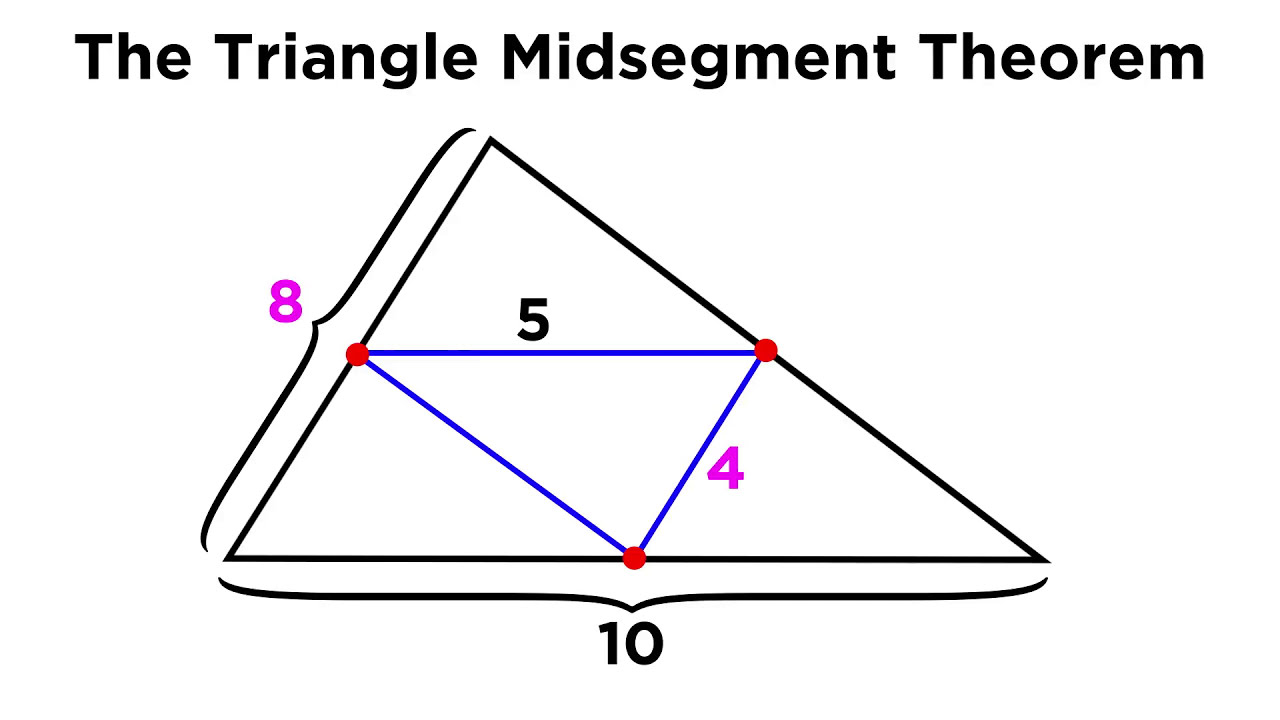
U6: Midsegments of Triangles

Segment between midpoints of 2 sides of a triangle, they are parallel to the opposite side and are half the length of the side they are parallel to

• if all midsegmnets are constructed, the perimeter is ½ the actual permimiter

U6: If a paralleogram has congruent diagonals, its a _______ If it has perpendicular diagonals, its a ____, if both it is a ______.

Congruent = Rectangle

Perpendicular = Rhombus

Both = Square

U6:

U6: Consecutive Angles

Angles in a polygon next to eachother are called consecutive angles, which are supplementary.

U7: Tangent Line

Intersects a circle or curve at 1 point

U7: A polygon is ______________ in a circle if and only if all vertices are on the circle

inscribed

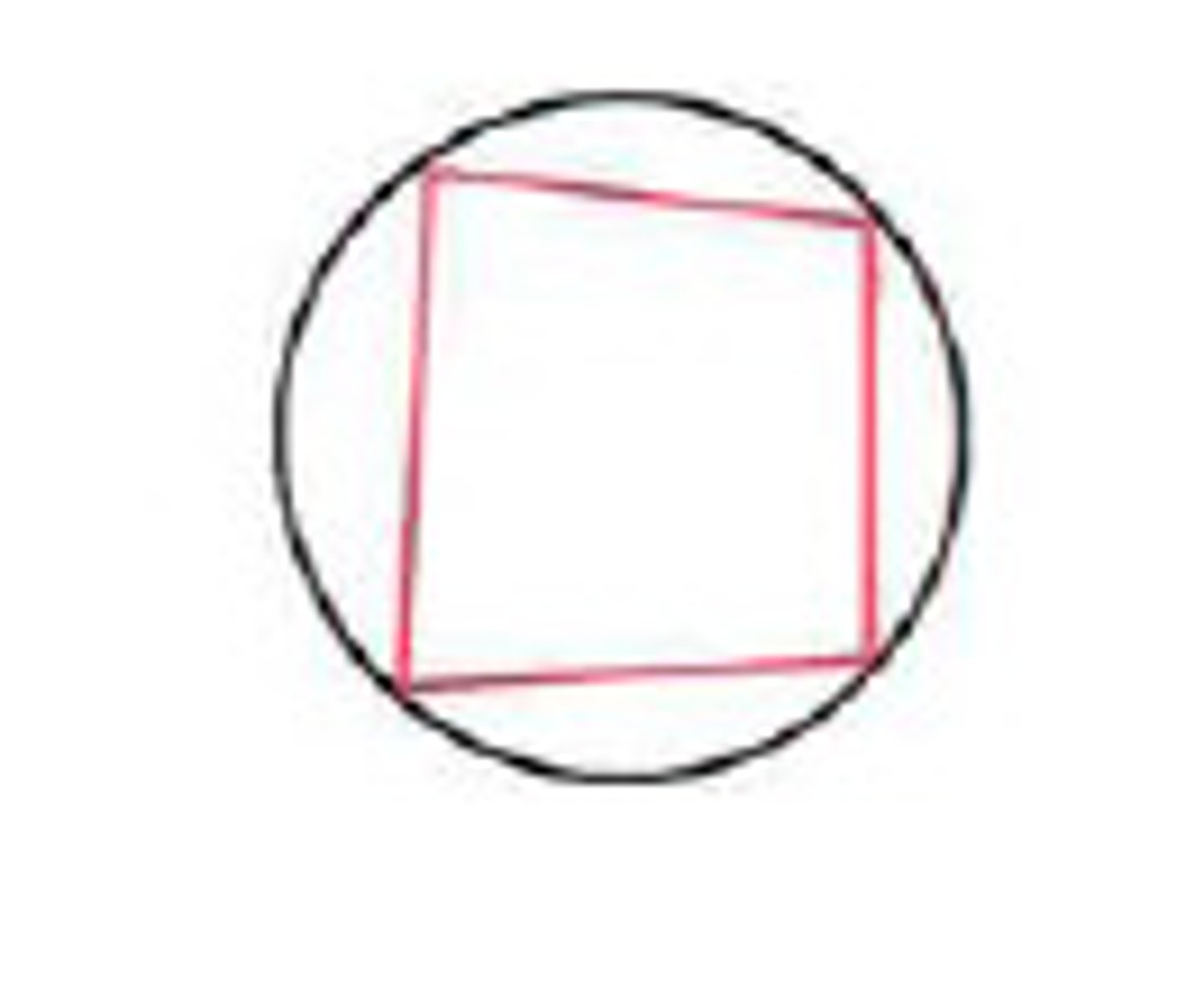
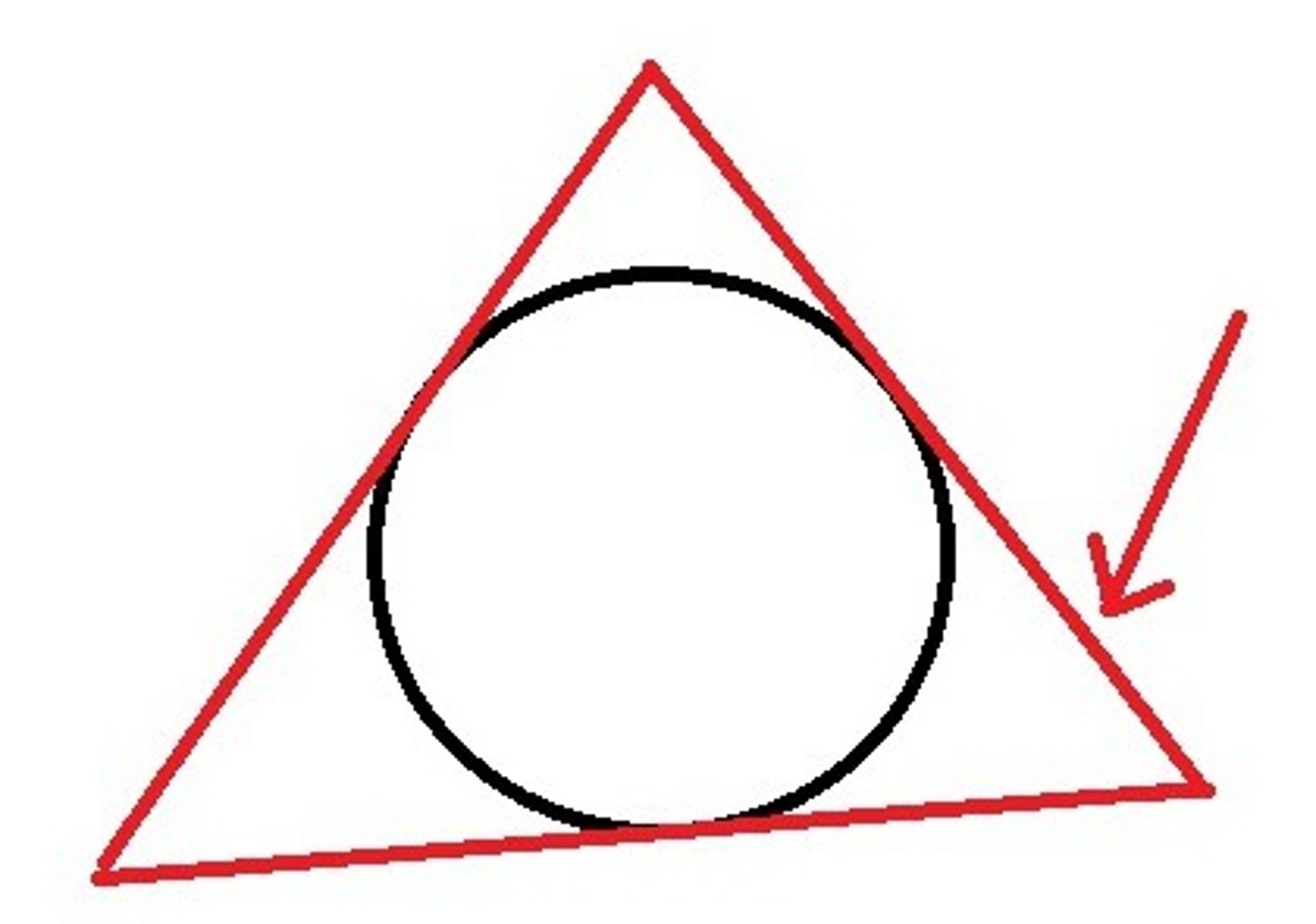
U7:A polygon is ____________ about a circle if and only if all sides are tangent to the circle

Circumscribed

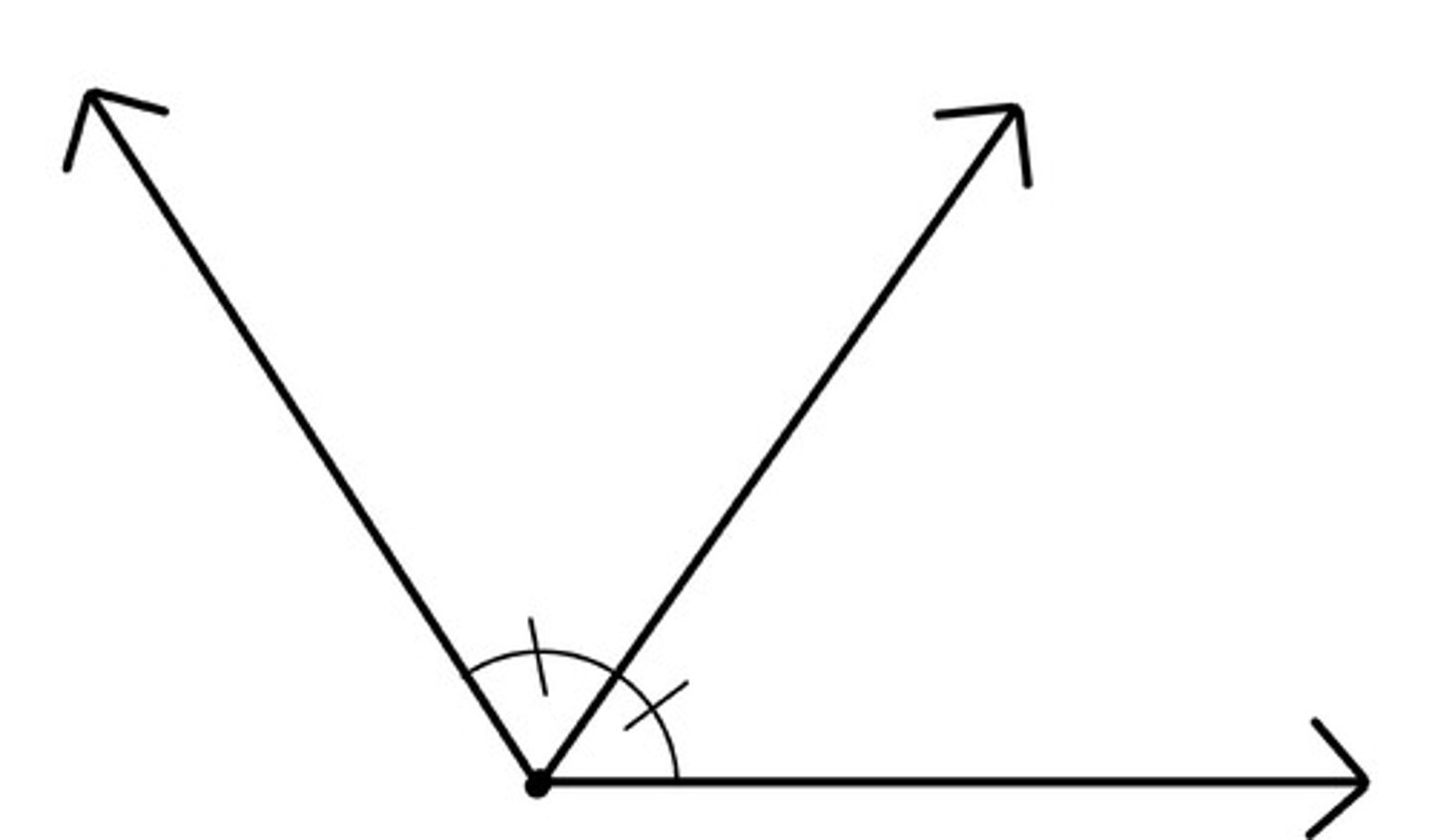
U7: Angle Bisector

The set of all points equidistant from two rays

U7: Perpendicular bisector

Set of all points equidistant from two endpoints