[MMW]: MODULE 2: DATA MANAGEMENT

Descriptive Statistics

Deals with the organization, presentation, and analysis of data to describe, show, or summarize data in a meaningful way; includes measures of central tendency, variation, position, and graphical presentation.

Inferential Statistics

Concerned with making inferences from a sample and generalizing them to a population; involves comparing, testing hypotheses, and predicting outcomes.

Descriptive statistics summarize and present data, while inferential statistics use data to make predictions or generalizations about a larger population.

What is the difference between descriptive statistics and inferential statistics?

Data Presentation

summarizing, organizing, and communicating data using tables, diagrams, charts, and statistical graphs.

frequency distribution, line graph, bar graph, pie graph, and scatter plots.

Statistical tools (5)

Statistical graphs

used to determine patterns or trends of data.

Time Series Graph

represents data over a specific period. It can be used to find out patterns or trends in the data. Two or more data sets can be compared.

Bar Graph

uses horizontal or vertical bars whose heights or lengths represent frequencies. It can be used to compare the data for two or more groups.

Pie Graph

a circular graph divided into sectors or wedges according to the percentage of the frequency. It can be used to show the relationship of the parts to the whole.

Scatter Plot

a graph of ordered pairs (x, y) that is used to describe the relationship between two variables.

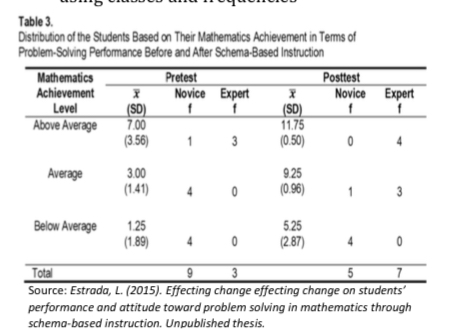
Frequency Distribution

organization of raw data in table form using classes and frequencies.

Parameter

a characteristic or measure obtained from all values in a population.

Statistic

a characteristic or measure obtained from the values of a sample of the population.

A parameter describes a whole population, while a statistic describes just a sample of that population.

What is the difference between parameter and statistic?

Mean (Arithmetic Average)

denoted by x̄ (sample ___) or μ (population ___). The ____ is computed by summing all the data values and dividing the sum by the number of values.

Weighted Mean

used when the values in a data set are not equally represented. Multiply each value by its corresponding weight, sum these products, and divide the sum by the sum of the weights.

Mode

the value that occurs most often in a data set. It is denoted by x̂. The data set can be unimodal (one mode), bimodal (two modes), multimodal (more than two modes), or have no mode at all.

Median

the middle value of a data set when the values are arranged in either ascending or descending order. It is denoted by x̃. If even number of values, the mean of the two middle values.

M, Mdn

In APA format, mean is symbolized by _ . Median is _.

Range (R)

the difference between the highest and lowest values in the data set.

Variance

the average of the squared distances of each value from the mean. Denoted by σ² for the population variance and s² for the sample variance.

Standard Deviation

the square root of the variance. Denoted by σ for the population _____ and s for the sample _____.

Hypothesis Testing

is a process in inferential statistics used to make decisions or draw conclusions from data. It’s like a court trial—assume something is true (null hypothesis) until evidence shows otherwise (alternative hypothesis).

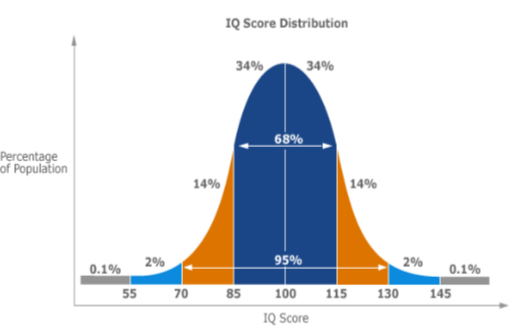
normal distribution

is a continuous, bell-shaped curve

One-tailed test

used when H₁ has > or <.

Two-tailed test

used when H₁ tests for difference (≠).

• Nominal

• Ordinal

• Interval

• Ratio

Scales of Measurement (5)

Nominal

Scales of Measurement: names/categories (e.g., shirt colors)

Ordinal

Scales of Measurement: ranked order (e.g., military ranks)

Interval

Scales of Measurement: equal spacing, no true zero (e.g., temperature °C)

Ratio

Scales of Measurement: equal spacing, true zero (e.g., weight, income)

• Normality of data

• Scale of measurement (nominal, ordinal, interval, ratio)

• Purpose (relationship, comparison, difference)

Choosing a Statistical Test

The test depends on: (3)

1 State the null hypothesis and alternative hypothesis

2 Set the level of significance and determine the direction of the tests

3 Collect data

4 Calculate a test statistic and determine the critical value

5 Decide on the rejection or acceptance of null hypothesis

6 Draw a conclusion

Steps in Statistical Hypothesis Testing (6)

Hypothesis

is an assumption, a claim, or a proposed explanation for an observation or phenomenon.

Null Hypothesis

is a claim that indicates the absence of relationship or difference between two values, denoted by symbol Ho

Alternative Hypothesis

is a claim that indicates the presence of relationship or difference between values, denoted by symbol Ha or H1

Hypothesis Testing

is a decision-making process for evaluating or testing claims about a population based on information obtained from samples

Level of Significance

is the maximum probability of committing type I error, denoted by the Greek alphabet alpha (𝛼)

Type I Error

occurs when a true null hypothesis is rejected, a.k.a. Alpha error

Type II Error

occurs when a false null hypothesis is accepted or not rejected, a.k.a. Beta error

One-Tailed Test

is a test that indicates that the null hypothesis should be rejected when the test statistic value is in the critical region on one side of the mean, a.k.a. directional test

Two-Tailed Test

is a test that indicates the null hypothesis should be rejected when the test statistic value is in either of the two critical regions, a.k.a. non-directional test

Confidence Level

is the probability that a parameter lies within the specified interval estimate of the parameter

Critical Value

is a value that separates a critical region (rejection region) from acceptance region in a hypothesis test, usually presented in tables

Statistic

is a value obtained by using all data value of a sample from a population.

▪ Z-test for one sample mean

▪ T-test for one sample mean

▪ Paired t-test

▪ Independent t-test

▪ Pearson product moment correlation

coefficient or Pearson’s r

▪ Analysis of variance (ANOVA)

▪ Linear regression

Parametric Tests (7)

▪ Chi-square test

▪ Spearman rank correlation

▪ Wilcoxon sign-rank test

▪ Sign test

Nonparametric Tests (4)