6.2: Applications in Business and Economics

This is the formula we use for a continuous income stream, which helps find the total income during a period of time

What is the formula for total income?

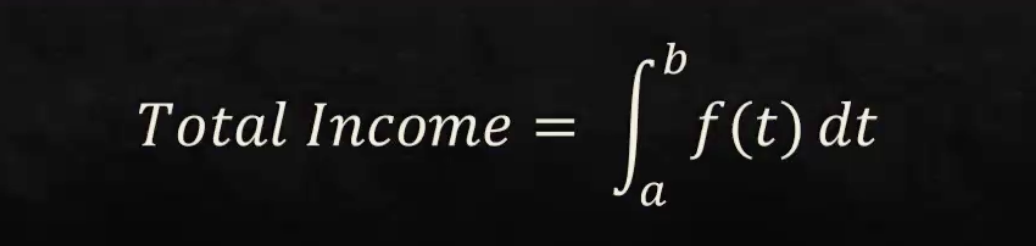
The formula for consumer surplus

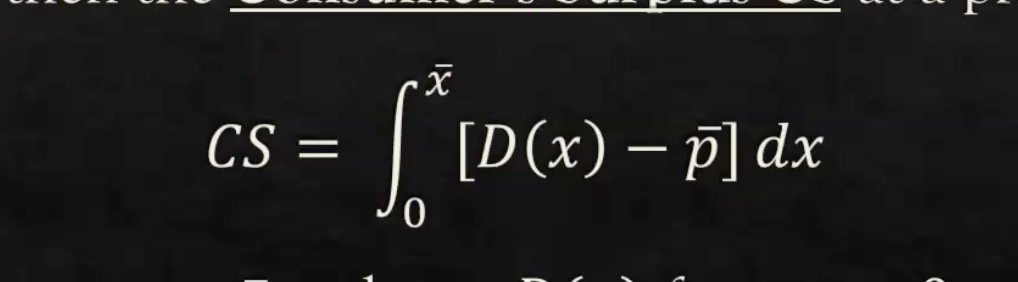
The formula for producer surplus

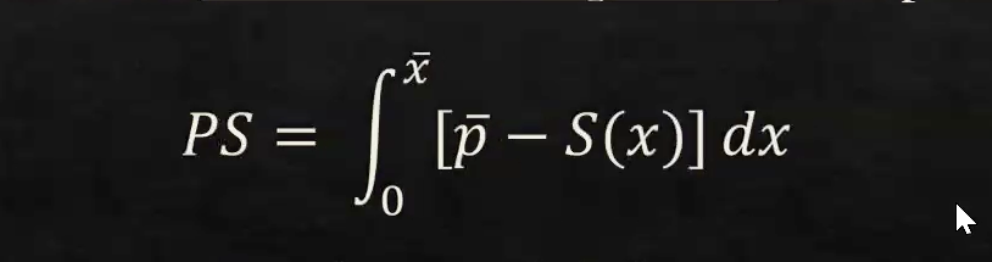
What is P bar called?

What is the equilibrium price

What is X bar called?

What is equilibrium quantity

Finding the real numbers

Steps

1) e^0.07t e^ 2.24 e^-0.08t

2) Simplify: e ^ 2.24 e^-0.01t

3) B= e ^ 2.24

4) C= e ^ -0.01t

Evaluate the following integral:

Steps

1) Substitute the 0.07 into (8-t) → e ^ 0.56, e^ -0.07t

2) Use MTH 9 to get → 10.72

How come A and C are equal and B isn’t?

A and C

1) When you evaluate, you get the same answers; however, you pull e^ 0.21 to the outside of the integral.

Why not B?

1) We are multiplying, not subtracting

A) Probability that product will fail in one year.

Steps

1) Since t is → Months: The integral for year one is 0 → 12

2) 0→12: 0.009e^-0.011t dt, into MTH 9 = 0.101

B) Probability that products fails 2nd year

Steps

1) Since we are taking about year two: 12→24 (integral)

2) 12→24: 0.009e^-0.011t dt , into MTH 9= 0.190

Find the total income in first 5 years.

Steps

1) From first five years: Integral: 0→5

2) 0→5: 4000dt = 20,000

Find the total income in first 3 years

Steps

1) From first three years: Integral: 0→3

2) 0→3: 700e^0.05t

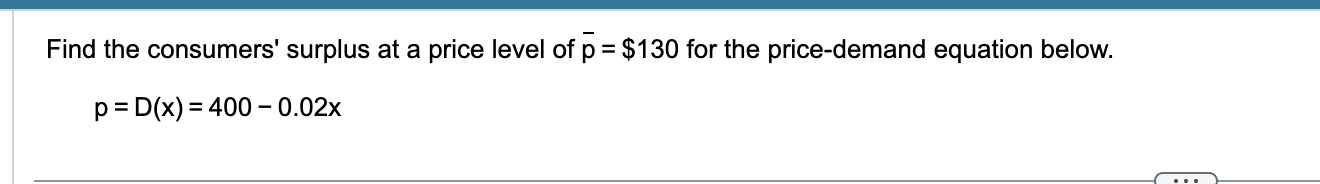
Find consumer surplus at price level (P bar) $130

Steps

1) Price-demand: 130= 400-0.02x

• 400- 130: 270= 0.02x

• x= 13,500 (X-Bar)

2) Consumer Surplus formula

• 0→ (X-bar); Dx -P bar

• 0→13,500: [ 400-0.02x -(130) ] = 1,822,500

What is the value of x, x Bar

Steps

1) D(x) =S(x)

• 29-0.04x=13+0.04x → 16=0.08x → x= 200

What is the value of p, p Bar?

Plug the value of X (200) into one of the equations.

• 29-0.04(200) = 21

Find Consumer Surplus

0 → x Bar: D(x) -P Bar

• 0→ 200: 29-0.04x -(21) = 800

FInd Producer Surplus

0→X Bar: P Bar- S(x)

• 0→ 200: 21- (13+0.04x) = 800