Physics 1 Lab 9: Simple Harmonic Motion

The defining characteristic of the restoring force in Simple Harmonic Motion

The restoring force is directly proportional to the displacement (x) from equilibrium and acts in the opposite direction of the displacement.

The relationship between restoring force (F) and displacement (x) for a spring

Hooke's Law: F=−kx, where kis the spring constant.

Formula for the Period (T) of a mass (m) on a spring (SHM oscillator)

T = 2\pi \sqrt{\frac{m}{k}}

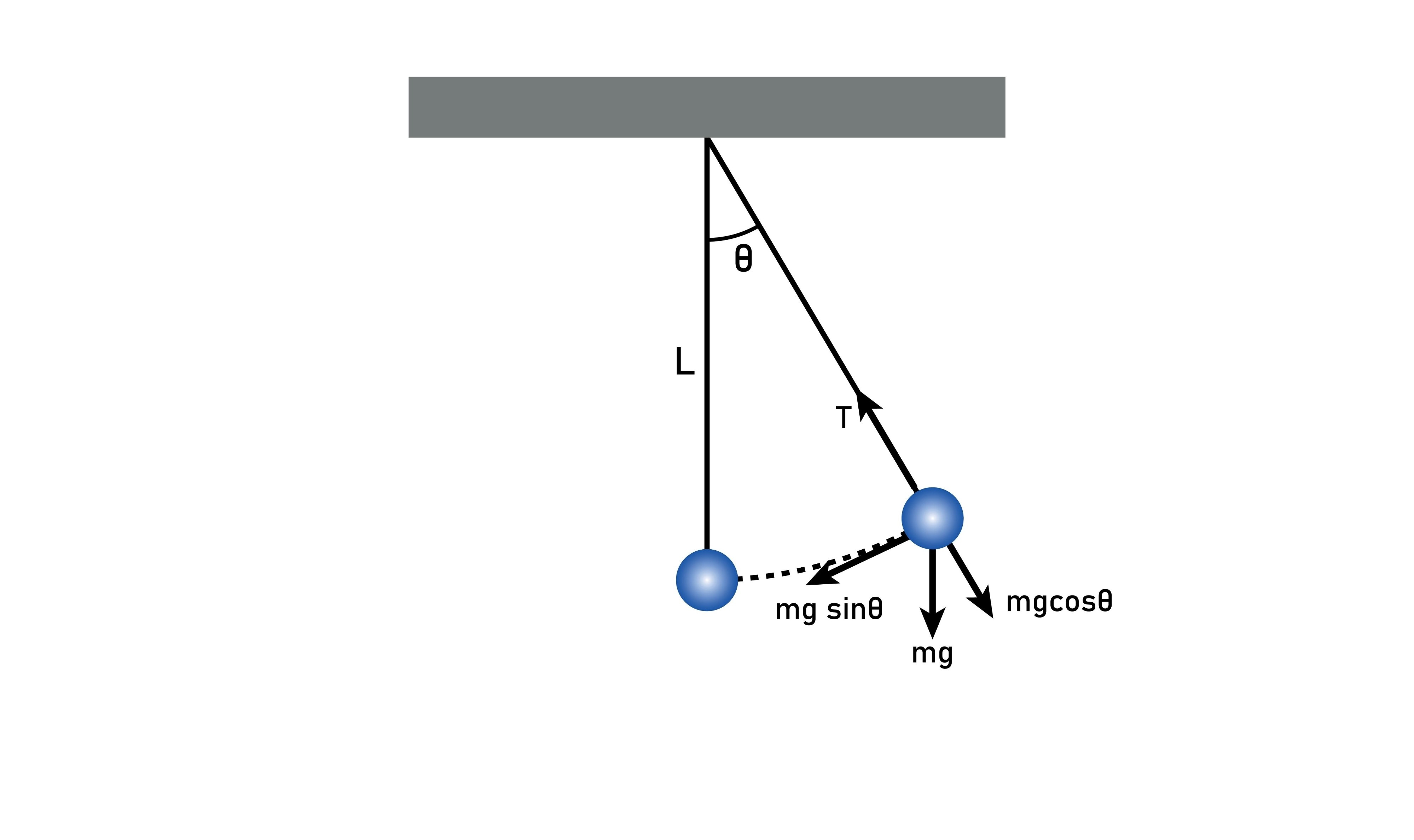
Formula for the Period (T) of a simple pendulum (for small angles)

T=2πsqroot(L/g)

Where L is length and g is gravity

Two factors that affect the Period (T) of a mass-spring system

The mass (m) and the spring constant (k).

What the amplitude (A) of SHM is

The maximum displacement of the object from its equilibrium position.

How frequency (f) relates to period (T)

Frequency is the reciprocal of the period: f=1/T

Where the maximum speed (vmax​) of an SHM oscillator occurs

As the object passes through the equilibrium position (x=0).

The relationship used in the mass-spring lab to determine k from a linear graph (Plotting T² vs. m)

From T²= 4π m/k, slope of graph is 4π²/k

The purpose of using the Hooke's Law method (F vs. x) in the SHM lab

To determine the spring constant (k) by measuring the static stretch from an applied force: ∣Fspring​∣=ks.

Relationship between angular frequency(ω) and the spring properties (m,k)

By comparison to d²x/dt²​=−ω²x, the angular frequency is ω=sqroot(k/m)

The period (T) of the motion, derived from the angular frequency (ω)

Since T=2π/w: T=2π sqroot(m/k)

Position of the mass at time t=T when starting at maximum positive amplitude (x=+A at t=0)

The mass is back at the maximum positive amplitude: x=+A.

Where the maximum force (Fmax​=kA) and maximum acceleration (amax​) occur

At the points of maximum displacement (amplitudes x=+A and x=−A).

The plot required for the Simple Pendulum part of the lab to find g (based on T=2πsqr(L/g))

Plot T² vs. L

What’s the equation in T² vs. L graph

T²= (4π²/g)L

What’s the slope in the T² vs. L graph

4π²/g

Units for the spring constant

N/m

What the quantity mobs (observed mass) reps in the mass-spring equation T²= (4π²/k)mobs

The total effective mass oscillating, which is the mass of the hanger/bob plus the effective mass of the spring itself.

The expected linear relationship found when using the static Hooke's Law method (F=-kx)

Plotting the applied force (mg) vs. the stretch (Δx) should yield a straight line whose slope is the spring constant (k).

The experimental relationship used in Method 1 (Hooke's Law) to determine the spring constant (k)

Plotting stretch (Δx) vs. mass (m), where the theoretical slope is g/k

What the intercept of the Δx vs. m graph should ideally be and why (Method 1)

The intercept should be zero, because if there is no mass, there should be no stretch (ideally).

The plot used in Method 2 (Dynamic) to find k from the period (T) of oscillation

Plotting the square of the period (T2) vs. the mass (m). The theoretical slope is 4π²/k

What the non-zero intercept of the T² vs. m graph (0.262) represents (Method 2)

The unaccounted mass of the spring itself (mspring​), as T² should be 0 when the added mass (m) is 0.

How the period (T) was measured in the dynamic (Method 2) experiment

Measuring the time for 10 oscillations, then dividing the number of seconds by 10.

for a block on a spring released from x= A where is the force max to the right?

x=-A (leftmost point, force is rightward)

how to linearize velocity from position data?

compute v= Δx/Δt

for a falling object on a strange planet if v(t)= 2t +0.5 what are a and v0?

a= 2 v0=0.5

hookes law

F= -kxnewtons second l

newtons second law for mass on ideal horizontal spring?

mx=-kx

where is the force mat and min in SHM?

max x=±A, min x=0SHM

SHM displacement equation

x(t)= Acos(2pit/T) or Acos(ωt)

how to find k without oscillation?

measure Δx and k=mg/Δx

how to find Δx using oscillatio period T and g?

T=2π sqr(Δx/g), so Δx= gT²/4π²

what is the slope of Δx vs. m?

g/k

what were the two methods of measuring k ?

static: hookes law Δx vs. m, and dynamic T² vs. m (oscillation period)

how is angular frequency related to k and m

ω= sqr(k/m)

T in terms of ω

= 2π/ω