RMA Week 9: Correlations and Chi-squared

what do scatterplots do?

display relations between two quantitative variables (and display correlations)

what’s the purpose of a correlation analysis?

to determine…

1. whether there’s a linear relationship between two variables (no curved lines of best fit!)

2. the direction of the relationship

3. the strength of the relationship

for Pearsons (r) and Spearmans correlation coefficient (r-mini down ‘s’), where do the values lie?

between -1 and 1

what are the different ways you can interpret r (rs)?

perfect positive +1, v.strong positive +0.95, positive +0.5, none 0, vv for negative correlations

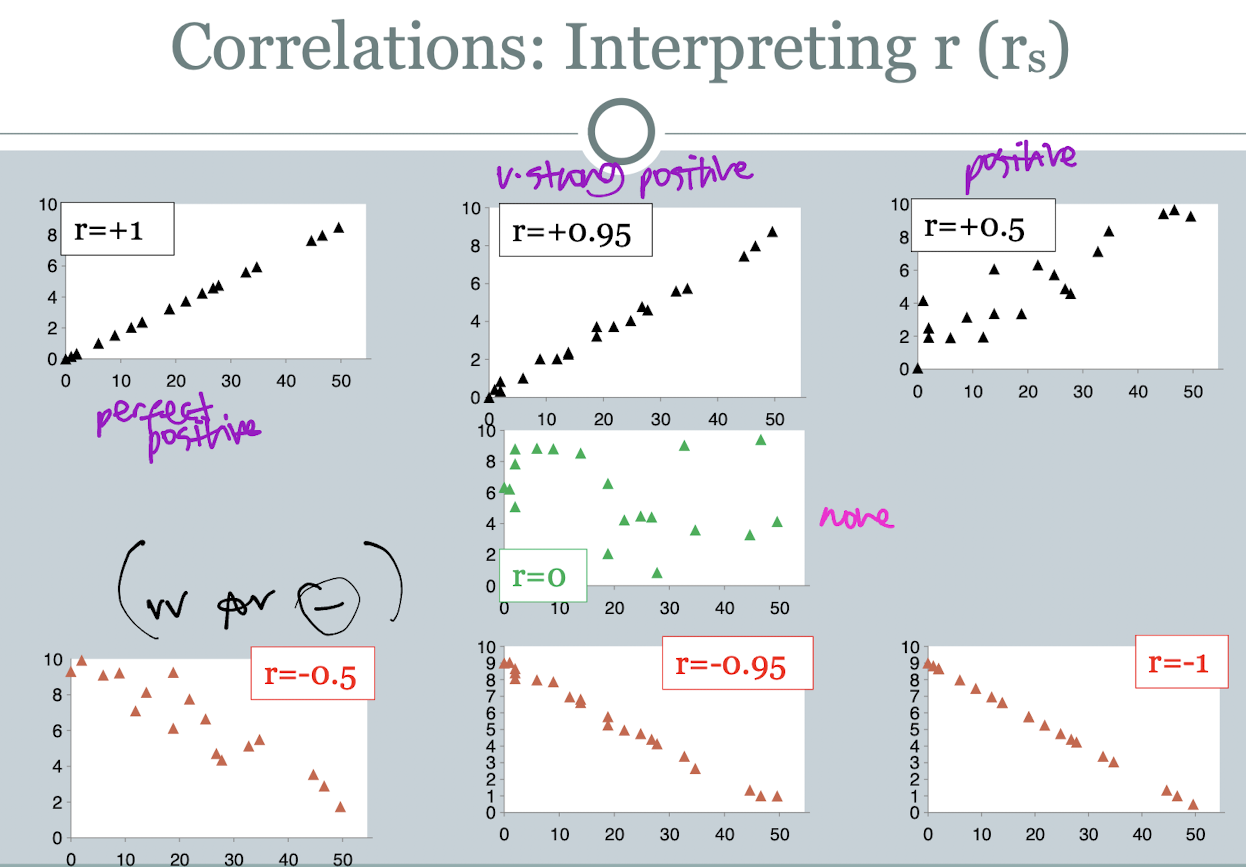
do correlations make a distinction between the IV and DV?

no

what happens to the correlation coefficient if we change the units of measurement?

it doesn’t change

what might we need to do if the data is curved and non-linear?

transform the data

describe the pearson r correlation coefficient

• calcuated directly from the raw scores

• suitable for interval or ratio data

advantage of pearson r correlation coefficient

it’s more powerful, try to carry it out more often

disadvantages of pearson r correlation coefficient

• highly affected by outliers

• not suitable for skewed data

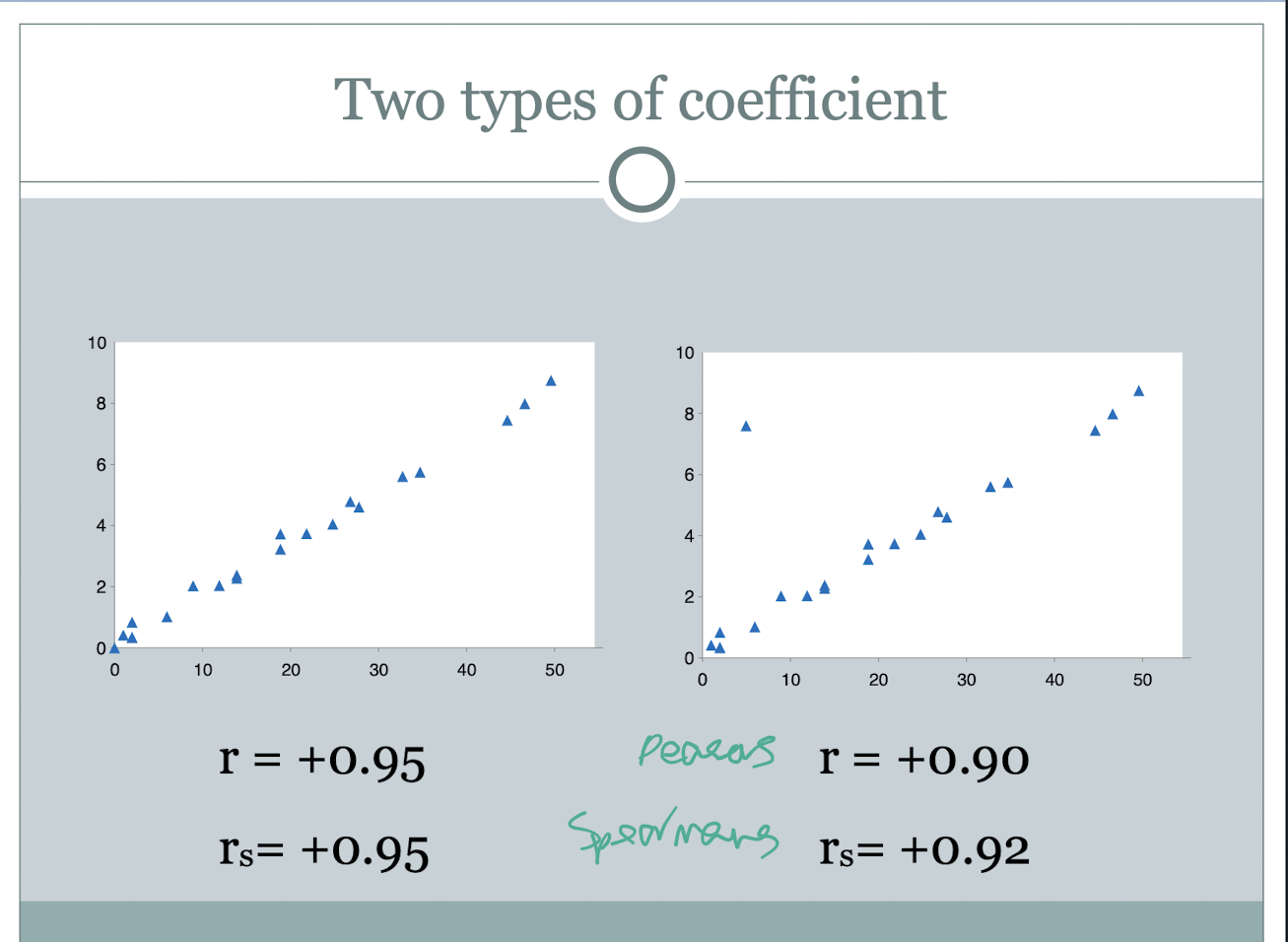
describe spearman rs correlation coefficient

• calcuated from the ranking of the raw scores

• suitable for ordinal data

advantages of spearman rs correlation coefficient

• marginally affected by outliers

• suitable for skewed data

what can we conclude from a correlation coefficient regarding sample size?

• when n is low, pattern may arise without real relationship.

• when n is higher (e.g. 10), pattern is unlikely to arise without a real relationship

is chi-square parametric or non-parametric?

non-parametric

what are the two types of chi-2 tests?

1. the goodness of fit test (GF)

2. the test of independence (TI), (transforms nominal to categorical data)

describe parametric tests

• they test for significant differences between data sets

• they make assumptions about population parameters (i.e. are distribution dependent)

• they require interval or ratio data

what happens in parametric tests if the tests assumptions are violated?

erroneous interpretations of data

describe non-parametric tests

• they test for significant differences between data sets

• they make no assumptions about population parameters (i.e. are distribution-free tests)

• they use nominal data

advantage of using non-parametric tests

they’re more robust

disadvantage of non-parametric tests

they’re not as powerful

what is the chi-square test for goodness of fit (x2) used to do?

1. used on unrelated data. every participant/case yields data for only one category

2. used to answer questions about the proportions of a population distribution e.g. is there gender bias in the psych dept?

3. used to compare different levels of one variable

4. compares the sample proportions to population proportions as specified by H0.

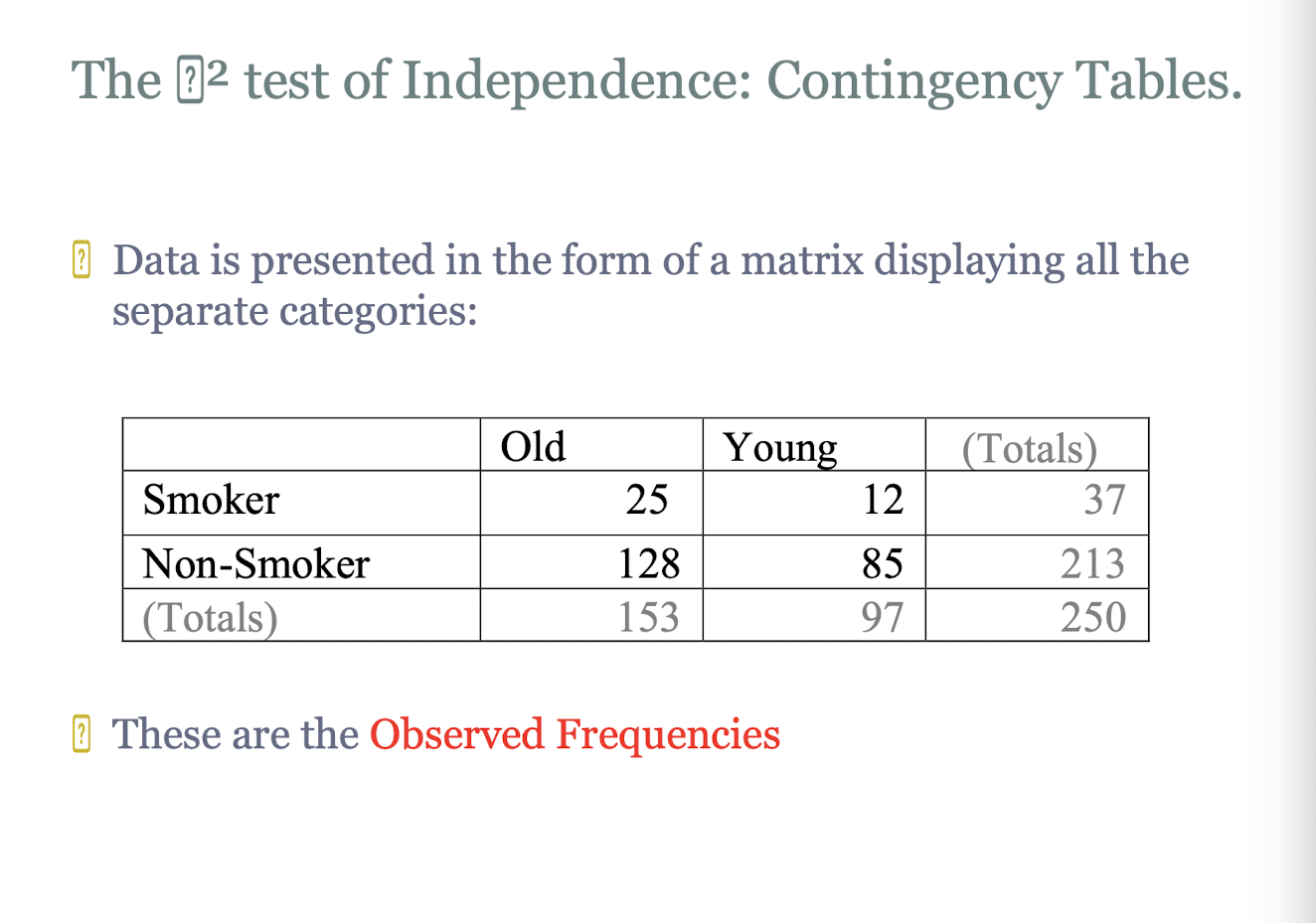
for X2, what is the observed frequency

the numbers of participants measured in individual categories

for X2, what is the expected frequency

frequencies predicted by the null hypothesis = chance alone

how could the expected frequency differ?

because it reflects the null hypothesis, changes in the null can change the expected frequency

how do you calculate X2?

for each category (e.g. men, women…)

1. subtract the number of cases expected from the number of cases observed

2. square this difference

3. divide the results by the number of cases expected

4. add all the results from all the categories

how do you calculate the degrees of freedom for X2?

df = C (cells in a table (in Jamovi)) -1

what’s the probability threshold for X2

p < 0.05

what does the chi-squared test of independence (TI) want to find out?

are two variables independent or associated (e.g. - does age influence smoking frequency?)

what does the TI do that is the same as the GF?

uses data in the form of frequencies in different categories, which is compared to expected frequencies predicted from the null hypothesis

what has to be H0 for TI?

the two variables being measured are completely independent from each other and do not affect each other at all (e.g. there is no relationship between age and smoking behaviour/smoking behaviour is the same for both age groups)

what has to be H1 for TI? (two examples)

e.g. - there is a relationship between age and smoking behaviour / the proportion of smokers is different for young and old age groups

how is data presented in TI for observed frequencies?

in a contingency table, in the form of a matrix displaying all the separate categories

for TI, how do you calculate the expected frequency?

by multiplying the column total and row total, divided by the total sample

what is the TI formula?

the same as X2 GF

what does a bigger X2 value indicate?

that the result is more significant

how do you calculate the degrees of freedom for TI?

(number of rows R - 1) x (number of columns C - 1)