Chapter 6 - Theorems/ideas - Matrix Algebra

Properties of the Inner Product:

For vectors u, v, w, in Rⁿ and scalar c:

Guarantees:

Inner products behave nicely with addition/scalars and detect zero vectors.

This is used to prove orthogonality, lengths, projections, Gram-Schmidt

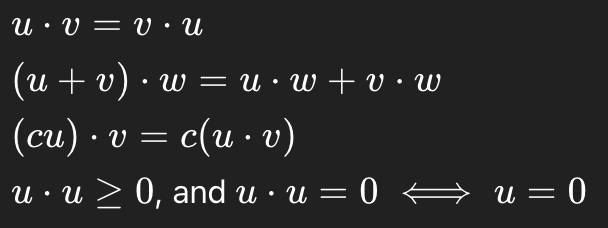
Pythagorean Theorem

Orthogonality → squared lengths add

Shows right angle algebraically, used in best approximation proofs

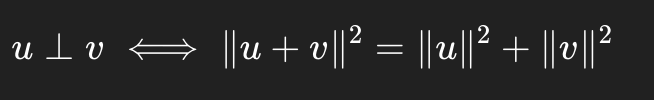
Othogonal sets are independent

If {u₁,…,u_p} is an orthogonal set of nonzero vectors, then it is linearly independent

Guarantees:

Orthogonal + nonzero → basis automatically

First way to prove basis without row reduction

Coordinates in an Orthogonal Basis

If {u₁,…,u_p} is an orthogonal basis for W and y in W

Guarantees:

Unique coordinates without solving systems

Used in projections, least squares, Gram-Schimdt

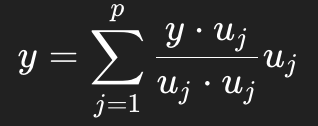
Orthonormal Columns Test

An m x n matrix U has orthonormal columns if:

• U^TU = I

Guarantees:

Quick test for orthonormality

Appears constantly in QR, projections, least squares

Orthogonal Decompostion Theorem

Every y in Rⁿ can be written uniquely as:

Guarantees:

Unique split into “in-subspace” + “perpendicular error”.

Foundation of least squares

Best Approximation Theorem

Guarantees:

Projection is the closest point in W

Explains why least squares works

Projection Matrix Formula

If U = [u₁…u_p] has orthonormal columns,

Guarantees:

Projections can be done with a matrix multiplication

fast projections; shoes projection matrices satist P² = P

Gram-Schmidt Process

Given a basis {x₁,…,x_p} Gram-Schmidt produces an orthogonal basis {v₁,…,v_p} spanning the same space

Guarantees:

Any basis → orthogonal basis

Required before QR and orthonormalization

QR Factorization

If A has linearly independent columns, then A = QR where:

• Q has orthonormal columns

• R is upper triangular with positive diagonal entries

Guarantees:

Every full rank matrix admits QR