Psychology statistics chapter 3

Flashcards for reviewing central tendency concepts in statistics.

Central Tendency

A statistical measure to determine a single score that defines the center of a distribution.

Mean (Official Definition)

The sum of scores divided by the number of scores; also known as the arithmetic average.

Population Mean (μ)

ΣX / N (sum of all scores divided by the number of scores in the population).

Sample Mean (M)

ΣX / n (sum of all scores divided by the number of scores in the sample).

example: 180/6 = 30

Mean (Alternate Definition #1)

The amount each individual would get if the total (ΣX) were divided equally among all the individuals (n) in the distribution.

ΣX/N

example:

Mean (Alternate Definition #2)

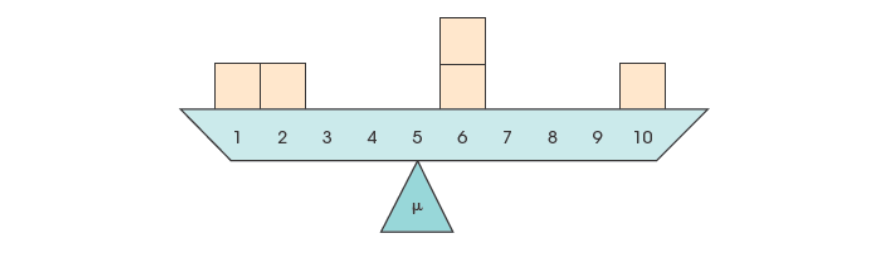
A balance point for the distribution. The total distance below the mean is the same as the total distance above the mean

example: balance point is 5

below the mean: 4+3=7

above the mean: 1+1+5=7

Weighted Mean

An overall mean calculated by considering the relative contribution of each score of 2 data sets. ΣX1 + ΣX2 / n1 + n2

overall sum of the 2 groups/total number in the 2 groups = overall mean

ΣX1 + ΣX2

• The overall sum of the 2 groups in the weighted mean calculation.

n1 + n2

the total number in the 2 groups in the weighted mean calculation

Median

The midpoint of the scores in a distribution when they are listed in order from smallest to largest; divides the scores into two groups of equal size.

Determining the Median when N is an odd number

a) Order the scores from lowest to highest
b) Identify the median as the score in the middle
c) It divides the score into exactly half

Determining the Median when N is an even number

a) Order the scores from lowest to highest
b) Locate the median by averaging the two middle score

Mode

The score (or category) that has the greatest frequency (occurs most often).

When to use the Median

a) Extreme scores or skewed distributions
b) Undetermined values
c) Open-ended distributions
d) Ordinal scales of measurement

When to use the mode

a) Nominal scales of measurement
b) Discrete/categorial values
c) Describing shape