Ch5 - Probability

the probability of any outcome of a chance process is

a number between 0 and 1 that describes the proportion of times the outcome would occur in a very long series of repetitions

sample space (S)

is the list of all possible outcomes

an event

is any outcome or set of outcomes of a random phenomenon

• an event is a subset of S

  • events are usually designated by capital letters, like A, B, C…

trial

is executing the random phenomenon (usually of a simulation)

probability model

is a mathematical description of a random phenomenon consisting of two parts: S and a way of assigning probabilities to the events in S

5 general probability rules

1. for any event A, 0 <= P(A) <= 1

2. If S is the sample space in a probability model, then P(S) = 1

   1. all possible outcomes together must have a probability of exactly one

3. In the case of equally likely outcomes

   1. P(A) = # of outcomes of event A / total outcomes in sample

4. The complement of any event A is the event that A does not happen, written as Ac. The complement rule states P(Ac) = 1 - P(A)

5. If A & B are mutually exclusive, P(A or B) = P(A) + P(B)

   1. two events are mutually exclusive (disjoint ) if they have no outcomes in common and so can never occur together - that is if P(A & B) = 0

General Rule for 2 events

if A and B r any two events resulting from some chance process then

P(A or B) = P(A) + P(B) - P(A & B)

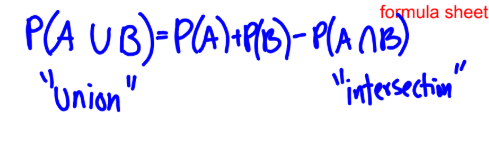
a simulation

shows the imitation of chance behavior based on a model that accurately reflects the experiment under consideration

Steps of running a simulation

1. P statement

2. Plan

   1. assign

   2. RNG

   3. record # of what u r looking for

   4. success statement Y/N

3. Do: trials using RandInt: Math → PRB → RandInt (#, - #, #)

4. Conclude (Y/N)

* Claim is never “defenitely true” no = only ~

“evidence to support the claim”

myths abt randomness

“randomness can be predictable in short run & the law of averages”

• no be coin has no memory, for any given toss chance is 50/50

conditional probability

the probability of an event occurring given that another event has already occurred

• P(A|B) = P(A and B) / P(B).

general multiplication rule

used to find the the likelihood of two dependent events occurring together.

• P(A and B) = P(B) × P(A|B)

tree diagram

visual rep of probs

• you can multiply down tree branches bc they are sequenced based on the general multiplication rule/conditional probability rule

• you can sum diff branches bc they are disjoint/mutually exclusive

independence

two events A and B are ___ if the occurrence of one event does not change the probability of the other (coin toss)

• P (A|B) = P(A) 

• P(B|A) = P(B)

multiplication rule for indep

if A and B are independent events, then the probability that A & B occur is 

• P (A and B) = P(A) x P(B)

if two events are disjoint..

they can NOT be independent

if two events are independent,

they are NOT disjoint

if an event is NOT disjoint

we don’t know anything abt independence

if an event is NOT independent…

we don’t know anything abt disjoint