data structures

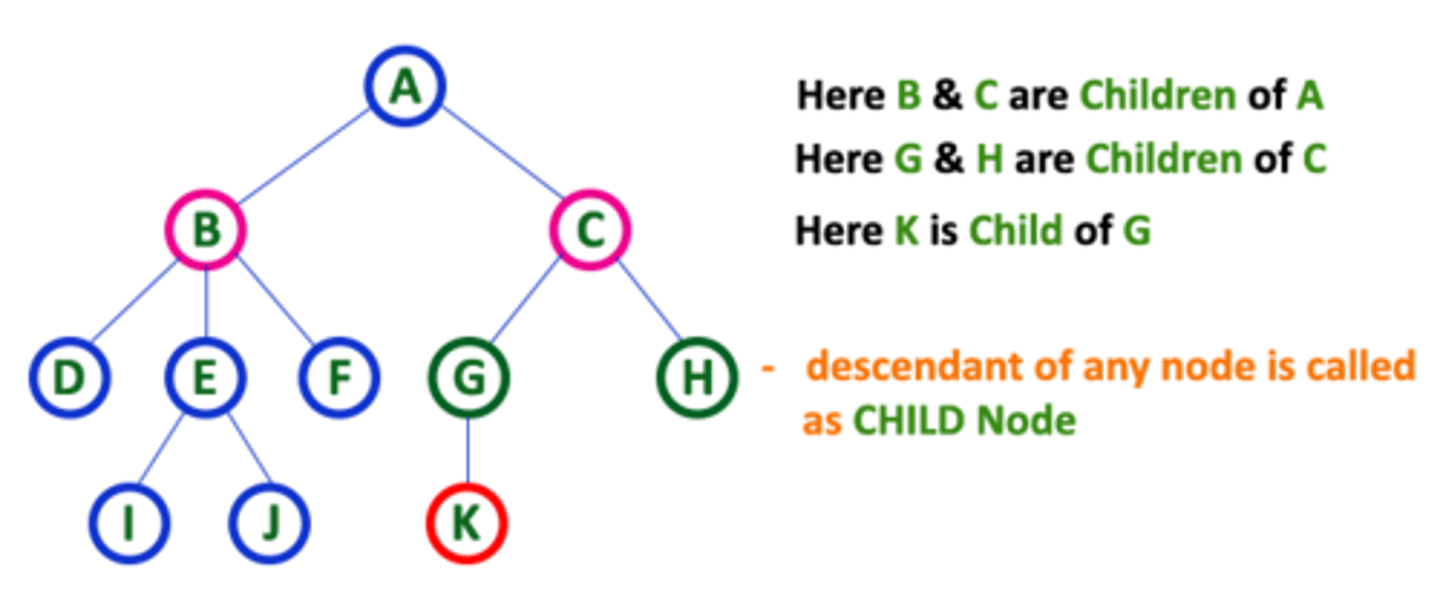
binary tree

a type of list where each node has up to two children (left and right child)

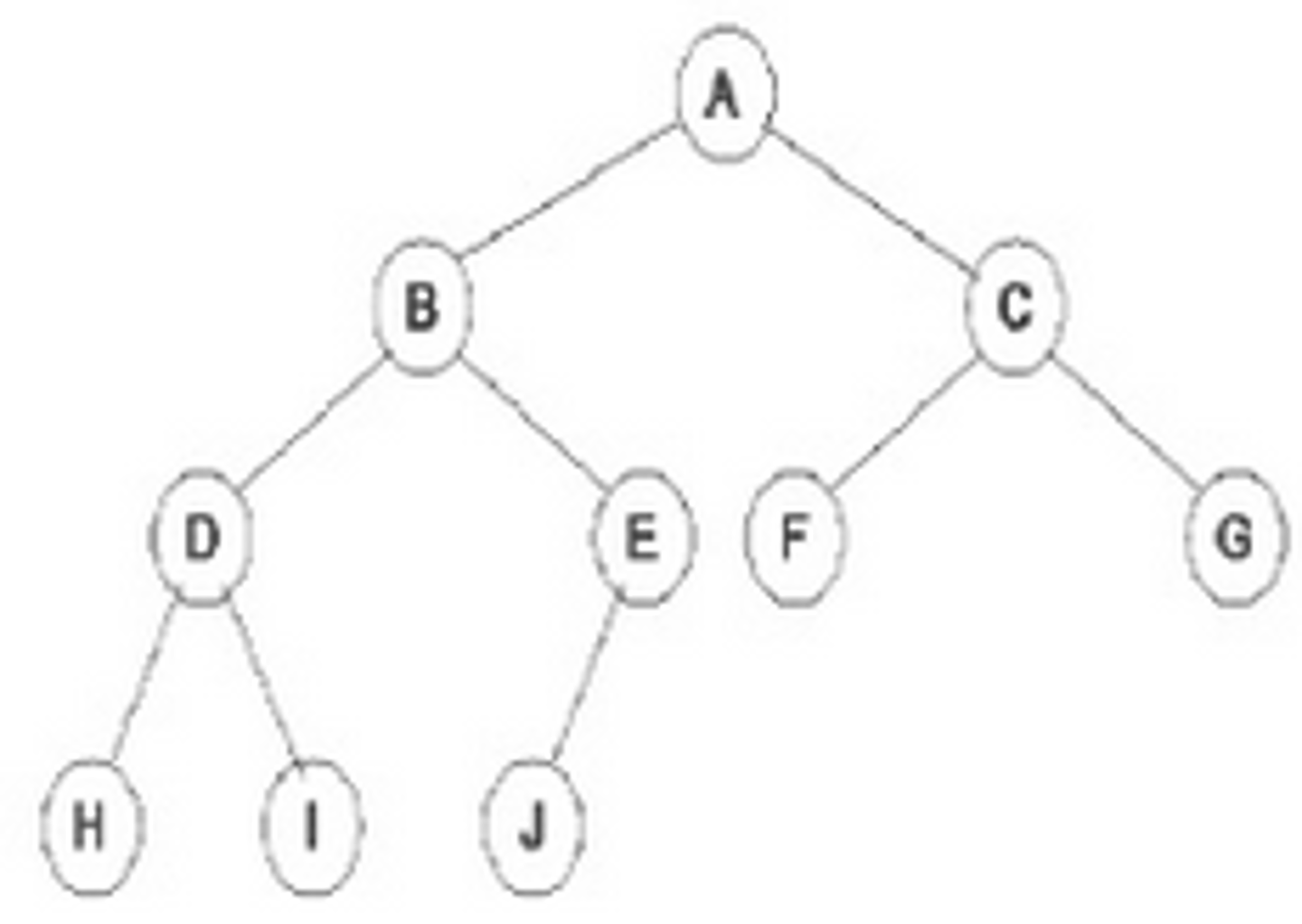
leaf

a tree node with no children

internal node

a tree node with at least one child

parent

a tree node that has a child node

ancestors

a tree node's parent and their parent and so on, until the root node is reached

root

a tree node with no parent (top node)

when considering internal nodes what is also included

the root node is included b/c it has children

edge

the link from a node to it's child

depth

the number of edges from the root node to a specified node

what will the depth of the root always be

zero

level

any nodes at the same depth on a tree

Height

the largest depth of the tree

full

a binary tree where every node has either zero or two children

complete

a binary tree where all the levels, with the exception of the last are full. the last level can be either full or have all of it's node be as far left as possible

what can a tree be used to represent

it can represent hierarchical data like files and directories in file systems

Binary Search Tree (BST)

a form of a binary tree that has an ordering property where any node's left subtree key is less than or equal to the node's key and vice versa for the right subtree

what is the runtime of a BST search

the worst case comparison is H+1 with a big-O notation of O(H), where H is the tree's height, this results in a tree with a runtime of O(log (base 2) N) where N is the number of nodes, however this will only be true when all but the last levels are full

successor node

node that will come after the current node based on the ordering property (smallest to largest

predecessor node

node that will be the node before the current node based on the ordering property (smallest to largest)

in a BST what is the successor node

the successor node is the current node's right subtree's leftmost child but if there is no right subtree then the successor is the first ancestor that has the current node as a part of the left subtree

in a BST what is the predecessor node

the predecessor node is the current node's left subtree's rightmost child but if there is no left subtree then the first ancestor of the current node is the predecessor (parent node)

what will the BST search algorithm return if it does not find a match

returns null

insert as a left child

if the new node is less than the current node and the current node's left child is null, then the current node's left child is set to the new node

insert as a right child

if the new node is greater than the current node and the current node's right child is null, assign the new node as the current node's right child

what is the complexity of the BST insert and remove algorithms

insertion for BST will visit one node per level with log(base 2) N levels to N levels, the best-case is O(log N) and the worst case is O(N). the space complexity is O(1)

how does a removal with BST work

the first matching node will be removed and the BST will be restructured based on the ordering property. how the tree is restructured depends on where the node is in the tree, if there is no match then null is returned

removal of a leaf node

if the found node has a parent then the subtree containing the found node is set to null, if the node was also the root then the root is null and the BST is empty

removal of an internal node with one child

if the found node has a parent, the subtree for the found node is assigned to the found node's child, if the found node is the root, the root is set to the child

removal of an internal node with two children

first locate the found node's leftmost child of it's right subtree, this will be the successor node, copy the successor node to the found node's location and recursively remove the successor node from it's original node

Tree traversal

a traversal algorithm that travels every node in a tree and preforms an operation on each node

inorder traversal

traverses the nodes from smallest to largest

how is the height of a binary tree found when it has a maximum N nodes

find the height with h = N - 1

for a BST how should the height be found

an empty subtree/nod is null and will return -1, using recursion, count the height of both the left and right subtree, then add 1 to the greater height to get the tree's height

what does each node in a BST implementation include

generally, a parent pointer so that a traversal can go down the tree and then back up to easily find a node's ancestors and siblings

what must be passed to a BST search algorithm that uses recursion

a single node and the search key

what is the first base case for a BST recursive search algorithm

if the node is null, the case will return null. If it is not null then the search key is compared to the node's key

what is the second base case for a BST recursive search algorithm

if the search key matches the node's key then the node is returned. if the search key is less than the node's key the left child is recursively called. if the search key is greater than the node's key, then the right child is recursively called

what algorithm is called if the BST nodes do not use parent pointers

BSTGetParent

how does BSTGetParentAlgorithm work

a recursive search is used to find the parent node by comparing a candidate node's child pointer to the search key.

can inserting and removing BST nodes use recursion

yes recursion can be used to traverse the tree until the appropriate node is found and the need operation carried out

Max-Heap

a binary (or any kind of tree) tree that maintains the property that requires a node's key is greater than of equal to it's children's keys

what does a max-heap ensure

it ensures that the tree's maximum key will always be the root key

percolating

any upward movement of a node in a max-heap

what is done to insert into a max-heap

insert at the heaps last level and then swapped with other nodes until it has a parent with a higher key. Note: last level should be fill from left to right and needs to be completely full before beginning a new level

what is done to remove from a max-heap

replace the root node with the last level's last (rightmost) node. then swap the replaced node down until it's parent is greater and it's children are less that it. Note: Always remove at the root node

min-heap

a type of tree where a node's key must always be less than or equal to it's children. Similar to max-heap

web server

a computer that provides web pages in response to internet requests

cache

copies of popular pages on a small fast drive

how are heaps usually stored

with arrays where the root node is at index zero, the left child at index 1, the right child at index 2, and so on

how are heaps stored

by traversing the tree's levels from left to right and starting at the top and then moving down by level

how are nodes traversed

traversal requires that nodes be referred to by their indices b/c heaps do not implement with node structure or parent/child indices

what is the formula to find a parent index

floor(( i - 1) / 2), where floor indicates to round down and i is the node's index

what are the formulas to find the child indices

left: 2(i) + 1, right: 2(i) + 2, where i is the node's index, always check to see if the children exist

heapsort

a sorting algorithm that takes advantage of a max-heap's properties by repeatedly removing the max and building a sorted array in reverse order

heapify

an operation used to turn an array into a heap, array must be in sorted order

how does heapify work

will start on the internal node with the largest index and will continue down to the root node (index 0). the largest internal node is found using floor(N/2) - 1, Note: leaf nodes are not checked with percolated down even if they are on different levels

will a sorted array make a valid max-heap

no a sorted array will not necessarily make a valid max-heap

what is heapsort runtime

worst-case runtime is O(N log N)

what is MaxHeapPercolateDown runtime

worst-case runtime is O(log N)

how many loops are used by heapsort

two loops are used

what does the first loop in a heapsort do

the first will heapify the array with MaxHeapPercolateDown, iterates (N/2) - 1 times

what does the second loop in a heapsort do

the second will remove the max value and store it at the end index, and then decrement down by one, iterates the arrayLength - 1 times

how is the number of iterations for a MaxHeapPercolateDown found

the first loop is found with (N/2) - 1, the second loop is found with arrayLength - 1, find the total number of iterations by adding the first loop plus one to the second loop

Priority Queue

a queue where every item has a priority with items that have a higher priority being closer to the front than ones with a lower priority

how does the push operation work with priority queue

inserts an item so that it is in front of the items with a lower priority

how does the pop operation work with priority queue

removes and returns the items with the highest priority, should be the first item

Push(PQueue, x)

inserts x after all equal or higher priority items

Pop(PQueue)

returns and removes the item at the front of the PQueue

Peek(PQueue)

returns but does not remove the item at the front of PQueue

IsEmpty(PQueue)

returns true if PQueue has no items

GetLength(PQueue)

returns the number of items in PQueue

PushWithPriority

special push operation where an item's priority is included as part of the call statement and will reside outside of the item itself

can a priority queue be implemented so that an item's priority does not have to be given

yes the priority queue can be implemented to determine an item's priority on its own

how do heaps work when implemented with a priority queue

the root node will have the highest priority.

what priority queue operations implemented with heaps have a worst case runtime complexity of O(log N)

push and pop operation

what priority queue opertations implemented with heaps have a worst case runtime complexity of O(1)

peek, isEmpty, and getLength operations

treap

a type of heap that uses a main key to maintain the BST ordering property along with a second, randomly generated key that maintains the heap property during insertions

what kind of tree does a treap usually produce and maintain

a balanced tree.

what are the basic treap algorithms

search, insert, and delete

what does the treap insert algorithms use to move a node

rotation is used to move the node after it has been inserted in order to maintain BST property. the original insert location is based on the main key and it's final location is found by percolating up with the heap property

how does the delete operation for a treap remove a node

the node is removed by resetting the node's priority (based on the kind of heap), percolating down with rotation until the node is a leaf to removing

what is the first way to delete in a treap

the first is to use a BST delete followed by a percolate down until the heap property is not violated

what is the second way to delete in a treap

the second way is to reset the node's priority key to a value based on the kind of heap (-infinity for max-heap), percolate down and delete the node once it becomes a leaf node, the percolation down is down with rotation so that the higher priority child is rotated up

which way is the considered better for treap delete

the second way is considered the better method

AVL Tree

a BST with a height balance property and a specific operations that will rebalance the tree when a node is inserted or removed

Height Balanced

for any node, the height of the subtrees is only different by zero or one

Balance Factor

for an AVL tree, when a nod's left subtree and right subtree heights are subtracted and equal to 1, 0, or -1. a non-existent subtree has a height of -1

does an AVL tree maintain minimum tree height

no it does not ensure that minimum tree height but it is more efficient for insertions and removals b/c it requires only a few rotations when rearranging

how is an AVL tree height found

AVL tree height is found with O(log N)

how is the maximum SVL tree height found

the maximum height of an AVL tree is 1.5 times the minimum height

what is a special ability of an AVL tree

it has the ability for each node to store the height of the subtree as a member. when an operation is preformed it may require for a node's ancestors to have their height rebalanced

rotation

a local rearrangement of a BST that will maintain the ordering property while rebalancing the tree

how happens for a right rotation with an existing right child

that child will become the left child of the rotated node (node moved into the right subtree) to maintain the BST ordering property. left rotation will be symmetrical.

what is requirement of a right rotation algorithm

requires that a subtree root must have a left child b.c the child pointers must be able to be reassigned

when should an ABL tree be rebalanced

if at any point where the balance factor is not 1, 0, or -1, generally occurs after insertions or removals and is preformed with rotations that will maintain BST ordering property

how many rotations does inserting inside of a subtree require

this will require a double rotation

what are the four imbalance cases

left-left, right-right, left-right, and right-left

what nodes will need to have their balance factors rebalanced when a node is inserted

only the nodes that are on the ascending path from the inserted node to the root

what are two methods to update a balance factor

recalculating the balance factor or having it stored as a data member and incremented by one when it is on the path from the new node to the root. the second method will increment plus on if ascending from the left child and minus one from the right child