ACFI310 - Lecture 5 Black-Scholes-Merton-Model

What are the key parameters in the Black-Scholes-Merton random walk assumption?

In a short period Δt, the stock return (ΔS/S) is normally distributed with:

• Mean: μΔt

• Standard deviation: σ√Δt

• Where μ is expected return and σ is volatility

What distribution does ST (Stock price at time T) follow?

ST is lognormally distributed because ln(ST) is normally distributed.

What are the mean and standard deviation of ln(ST)?

• Mean: ln(S₀) + (μ - σ²/2)T

• Standard deviation: σ√T

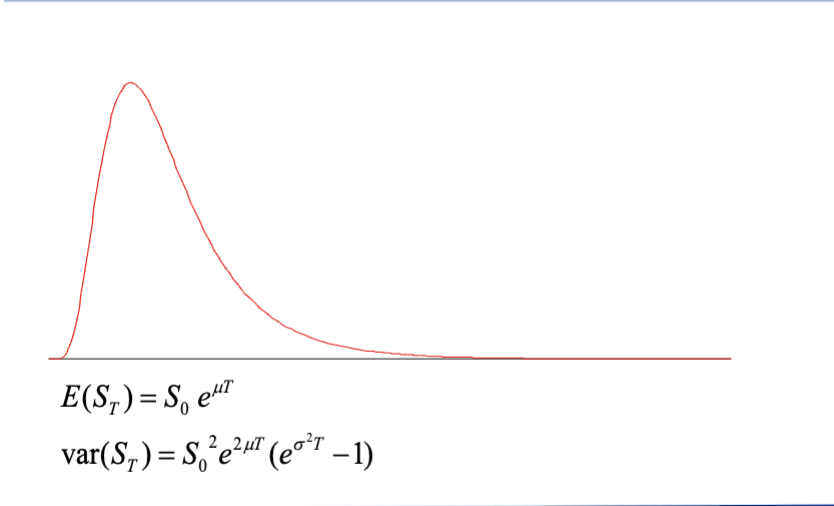
What is the expected value of ST?

E(ST) = S₀e^(μT)

What is the volatility in the Black-Scholes model?

The standard deviation of the continuously compounded rate of return in 1 year.

What is the standard deviation of return in time Δt?

σ√Δt

If a stock price is $50 with 25% annual volatility, what is the standard deviation of the price change in one day?

• Percentage change: 25% × √(1/252) = 1.57%

• Dollar amount: $50 × 1.57% = $0.785

How do you estimate historical volatility?

• Take observations S₀, S₁, ..., Sn at intervals of τ years

• Calculate continuously compounded returns: uᵢ = ln(Sᵢ/Sᵢ₋₁)

• Calculate standard deviation s of the uᵢ

• Annualized volatility: σ̂ = s/√τ

Why is time measured in trading days rather than calendar days?

Volatility is usually much greater when the market is open (asset is trading) than when it is closed.

What are the seven key assumptions underlying the Black-Scholes-Merton model?

• Stock price follows lognormal model with μ and σ constant

• No transaction costs or taxes; all securities perfectly divisible

• No dividends during option life

• No riskless arbitrage opportunities

• Security trading is continuous

• Investors can borrow/lend at same risk-free rate

• Short-term risk-free rate r is constant

What are the three key concepts underlying Black-Scholes?

• Option price and stock price depend on same source of uncertainty

• Can form portfolio of stock and option that eliminates this uncertainty

• Portfolio is instantaneously riskless and must earn risk-free rate

What are the Black-Scholes formulas for European call and put options?

• Call: c = S₀N(d₁) - Ke^(-rT)N(d₂)

• Put: p = Ke^(-rT)N(-d₂) - S₀N(-d₁)

What are d₁ and d₂ in the Black-Scholes formula?

• d₁ = [ln(S₀/K) + (r + σ²/2)T] / (σ√T)

• d₂ = [ln(S₀/K) + (r - σ²/2)T] / (σ√T) = d₁ - σ√T

What does N(x) represent?

The probability that a normally distributed variable with mean 0 and standard deviation 1 is less than x.

What does N(d₂) represent in risk-neutral terms?

The probability that the option will be exercised in a risk-neutral world.

What happens to call and put values as S₀ becomes very large?

• Call tends to: S₀ - Ke^(-rT)

• Put tends to: zero

What happens to call and put values as S₀ becomes very small?

• Call tends to: zero

• Put tends to: Ke^(-rT) - S₀

Why doesn't μ (expected return) appear in the Black-Scholes formula?

The equation is independent of all variables affected by risk preference, which is consistent with risk-neutral valuation.

What are the three steps for applying risk-neutral valuation?

• Assume expected return from asset is the risk-free rate

• Calculate expected payoff from derivative

• Discount at risk-free rate

How are European options on dividend-paying stocks valued?

Substitute the stock price less the present value of dividends into the Black-Scholes-Merton formula (same adjustment as put-call parity).

Which dividends should be included in option pricing?

Only dividends with ex-dividend dates during the life of the option.

What "dividend" amount should be used?

The expected reduction in stock price on the ex-dividend date.

When should an American call on a non-dividend-paying stock be exercised early?

Never. It should never be exercised early.

When should an American call on a dividend-paying stock be exercised early?

Only immediately prior to an ex-dividend date.

What is Black's approximation for American calls with dividends?

Set American price equal to maximum of two European prices:

1. Option maturing at same time as American option

2. Option maturing just before final ex-dividend date

What is implied volatility?

The volatility for which the Black-Scholes price equals the market price.

What is the relationship between prices and implied volatilities?

There is a one-to-one correspondence between prices and implied volatilities.

How do traders quote options?

Traders and brokers often quote implied volatilities rather than dollar prices.

What is the VIX Index?

The CBOE Volatility Index - a key measure of market expectations of near-term volatility conveyed by S&P 500 stock index option prices.

What is the difference between short-period return and continuously compounded return in Black-Scholes?

• Return in short period Δt: μΔt

• Expected continuously compounded return: μ - σ²/2

• This reflects difference between arithmetic and geometric means

The lognormal distribution

What happens to a call option value as S₀ → ∞?

Call → S₀ - Ke^(-rT). The option becomes deeply ITM and behaves like owning the stock minus the discounted strike price.

What happens to a put option value as S₀ → ∞?

Put → 0. The option becomes deeply OTM and worthless since the stock will almost certainly stay above the strike.

Why does a call option → S₀ - Ke^(-rT) when S₀ is very large?

When S₀ >> K, exercise is virtually certain. You'll pay K at expiration to get something worth ~S₀, so the option's value is the stock price minus the present value of the strike payment.

Intuition: Stock at $10,000, strike at $100. What are the call and put worth?

Call ≈ $10,000 - $100e^(-rT) (almost guaranteed profit). Put ≈ $0 (why sell at $100 when the stock is worth $10,000?).

How does put-call parity explain option behavior as S₀ → ∞?

Put-call parity: C - P = S₀ - Ke^(-rT). If P → 0 as S₀ → ∞, then C must → S₀ - Ke^(-rT) for the equation to hold.

What happens to call and put values as S₀ becomes very large?

Call → S₀ - Ke^(-rT) | Put → 0