PStats Exam 1

Population

Entire group of interest

Sample

Individuals selected to represent the population

Parameter

Value describing a population

Statistic

Value describing a sample

Descriptive Statistic

Summarize, organize, and simplify data

Inferential Statistic

Use sample data to make generalizations about the population

Constructs

internal attributes (intelligence) that can’t be directly observed

Experimental Method

Purpose: Demonstrate Cause & Effect relationship

Includes: Manipulation, control experiment (group that does not receive the treatment; serves as a baseline), and random assignment

Operational Definition

Defines constructs in measurable terms

Discrete Variable

(Whole numbers) No values between categories (# of children —> can’t have 2.5 kids)

Continuous Variable

(decimals) Infinite possible values (ex: height)

Variable

Characteristic/condition that changes (varies)

Data (plural)

Measurements/observations of a variable

Datum (singular)

one measurement (also called score)

Data Set

Collection of measurements

Nominal

(N=Name) Categories with names (no order)

Ordinal

(Ord - Order) Ordered categories, but differences are not measurable (small, medium, large)

Interval

Equal intervals, no absolute zero (ex: Temp)

Ratio

Interval scale Absolute Zero (ex: weight)

Manipulation

researcher controls level of independent variable

Independent Variable

Manipulated

Dependent Variable

Measured outcome

Descriptive Research

Measure 1 or more variables per individual

• Can use category or numerical variables

Correlational Method

Measure two variables in one group to see relationships

• Describe type and magnitude of relationship

• No cause and effect

Comparing Groups

One variable defines groups, another is measured

• Experimental and non-experimental 

ex: Violence/no violence vs aggressive behavior 

Frequency Distribution

Grouping together all individual scores that are the same

∑f = N

sum of frequencies = total sample size (N) (add up the amount of numbers - 1,2,3 n =3)

• Add up the total of Frequencies (4+1+2)

∑X

Sum of scores

• ∑f(X)

Multiply each X with their corresponding Frequency number, once you multiplied all numbers on the table, you add it together to get ∑X

What frequency distribution graphs are for Interval or Ratio data?

• Histograms

• Block histograms

• Polygons (line graphs)

What frequency distribution graphs are for Nominal or Ordinal data?

• Bar graphs

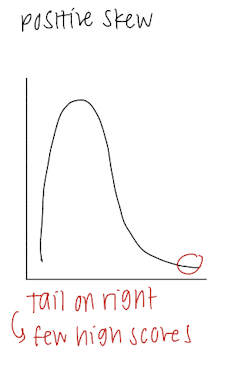
Positive Skew

Tail on right = fewer high scores

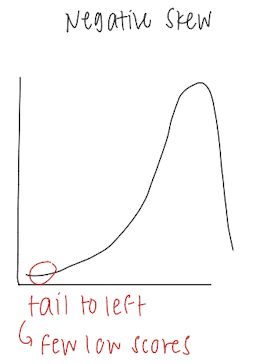
Negative Skew

Tail to the left = few low scores

What are the axis of the frequency distribution graphs?

Y = frequency

X = Scares

Mean

Sum of all scores divided by # of scores in data

Central Tendency

A single score that defines center of distribution

• Measures of central tendency: Mean, Median, Mode

Proportions (p)

Fraction of the group associated w/ each score
p= f/N

Median

middle score when data are ordered from smallest to largest

• If N (sample size) is odd —> middle score

• If N is even —> average two middle scores

Mean vs Median

Mean = median —> normal distribution

Mean > median —> positive Skew (tail right)

Mean < median —> negative skew (tail left)

• Outliers/skewed = use median

• # balances w/o extreme scores = use mean 

Mode

score or category that has highest frequency

When to use mean

• Calculate Sum of variables (∑X)

• Know value of every score

• Ratio Scale

• Interval Scale

When to use median

• Extreme scores

• Skewed distribution

• Undetermined Values 

• Open-ended distribution

• Ordinal Scale

When to use Mode

• Nominal scales

• Discrete variables (whole #’s only)

• Describing shape

Variability

measure how spread out scores are in a distribution, in terms of distance 

Standard Deviation

Average distance between individual scores and mean

Steps to find standard deviation

1. Find deviation score for each (x-µ)

2. Square each deviation score (x-µ)²

3. Sum the squared deviation SS = ∑(x-µ)²

4. Find variance

5. Find standard deviation

Sum of Squared Deviations

• Definitional Formula

• Computational Formula (only use when decimal #’s for the mean)

1. Find each deviation score (x-µ)

2. (x+µ)²

3. Sum of square deviation

Z-Scores

Tells us where a raw score (X) is located relative to the mean (population (µ) or Sample (M)) in units of standard deviation (𝞼 or S)

• Mean is ALWAYS 0

• Standard Deviation is ALWAYS 1

Z Score compared to mean

Z = 0 —> score is at the average/mean

Z > 0 —> Score is above average (+)

Z < 0 —> Score is below average (-)

Range

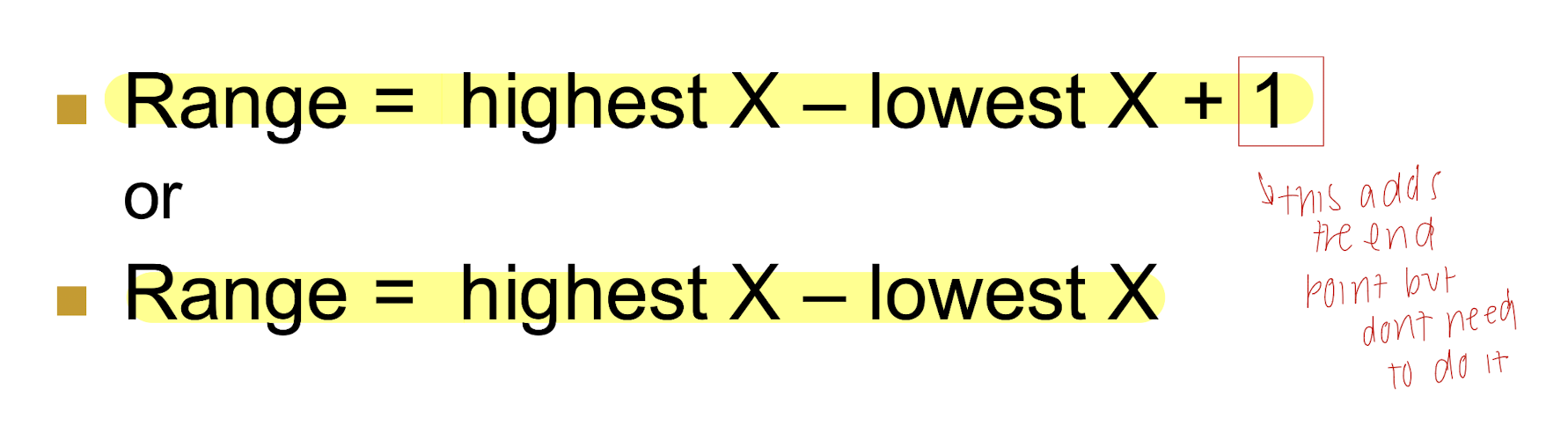
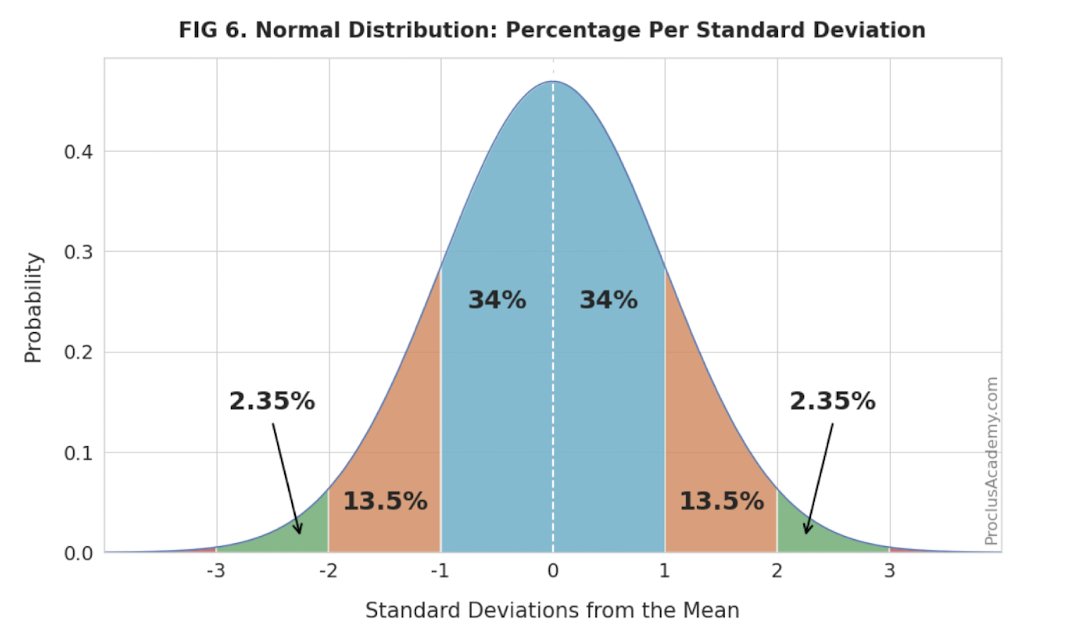
Normal Distribution

Control Condition

• Does not receive the treatment:

  This group serves as a point of comparison, acting as a baseline to show what happens without the experimental intervention. 

• Purpose:

  To rule out alternative explanations for the experimental results and isolate the effect of the independent variable. 

Experimental Condition

• Receives the treatment:

  Participants in this group are exposed to the independent variable, the factor that the researcher is manipulating or investigating. 

• Purpose:

  To observe the effects of the independent variable on the dependent variable.