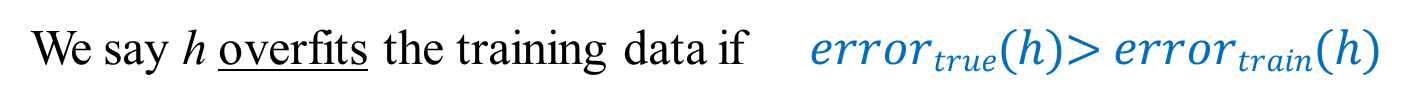Decision Trees
1/14
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
15 Terms
DT learning
Method for learning discrete-valued target functions in which the function to be learned is represented by a decision tree
Can have continuous or discrete features
Continuous features
Check if the feature is greater than or less than some threshold
The decision boundary is made up of axis-aligned planes
Internal nodes
test a feature
Branching
Determined by the feature value
Leaf nodes
outputs, predictions
Classification Tree
Discrete output
Goal with decision trees
We are guaranteed goof generalization if we are able to find a small decision tree that explains the data well
Choosing a good split
We could find the entropy of our training samples to generate our tree
Entropy formula:
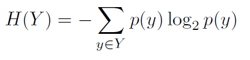
Entropy Rule of Thumb
High Entropy
Uniform like distribution over many outcomes
Flat histogram
Values sampled from it as less predictable
Low Energy
Distribution is concentrated on only a few outcomes
Histogram is concentrated in a few areas
Values samples from it are more predictable
If all Negative, entropy = 0
If all positive, entropy = 0
If 50/50 positive and negative, entropy = 1
Information Gain
Difference of the Entropy of our attribute, subtracted by the entropy of the attribute given the classification, in proportion to that attribute
The higher the IG for a particular category, the higher the precedence is given towards it
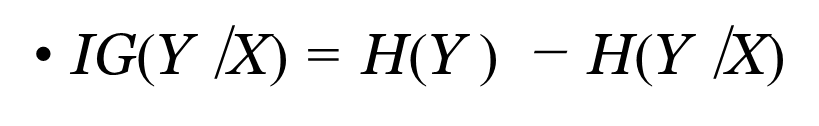
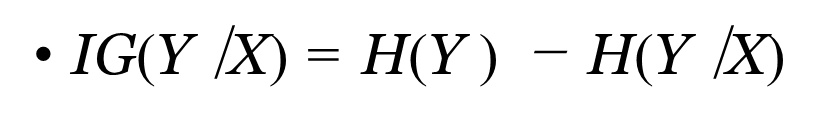
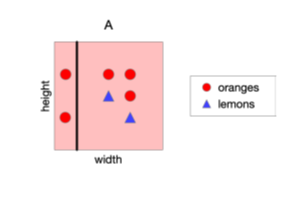
What is the Information Gain for this split? (Split A)
Steps:
H(Y) = -(5/7)log2(5/7)-(2/7)log2(2/7)
H(Orange|Left) = -(2/2)log2(2/2)-(0/2)log2(0/2)
H(Orange|Right) = -(3/5)log2(3/5)-(2/5)log2(2/5)
I.G = H(Y) - ((2/7)H(Orange|Left) + (5/7)H(Orange|Right))
Explanation: H(Y) is entropy of the split, H(Orange|Left) is the entropy of orange on the left, H(Orange|Right) is the entropy of orange on the right, I.G is the difference between the entropy of the split subtracted by the sum of the entropies of the regions proportional to how many elements in their domain compared to the whole.
Decision tree construction algorithm

What makes a good tree?
Not too small: Need to handle subtle distinctions in data
Not too big
Computational efficiency
Avoid Overfitting
We desire small trees with informative nodes near the root
Problems
You have exponentially less data in lower levels
Bigger the tree, the higher the overfitting
Greedy algorithm is not the most optimal solution
What do we consider overfitting