Geometry Circle Review

Central Angle

An angle whose vertex is at the center of a circle and whose sides are radii.

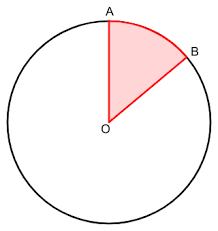
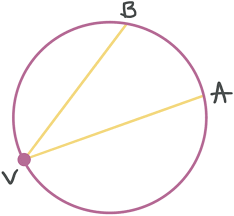
Inscribed Angle

An angle formed by two chords in a circle which have a common endpoint. The angle is half of its arc. It's the same as the measure of the arc subtended by it.

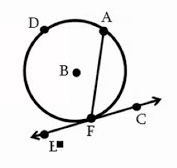
Tangent-Chord Angle

An angle formed by a tangent and a chord through the point of contact.

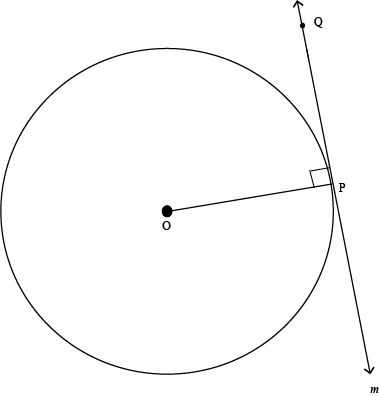
Perpendicular Radius

A radius that intersects a tangent at a right angle (90°).

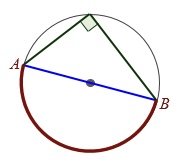
Inscribed Angle in a Semicircle

Always equals 90°

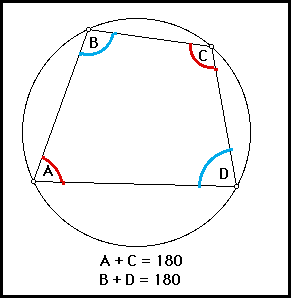
Quadrilateral Inscribed in a Circle

Has opposite angles that sum to 180°.

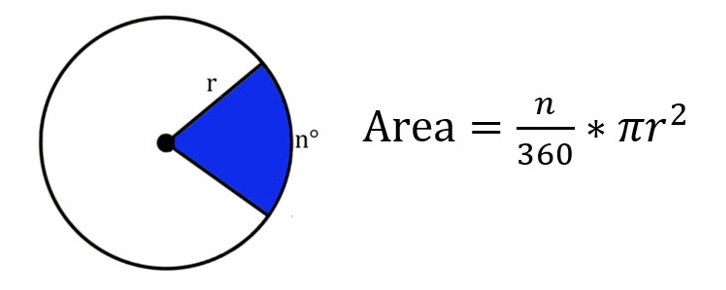
Area of a Sector formula

A = (n/360)πr^2

where A is the area, r is the radius, and θ is the angle in radians.

Sector Length

s= r * θ , where s is the length of the arc, r is the radius, and θ is the angle in radians.

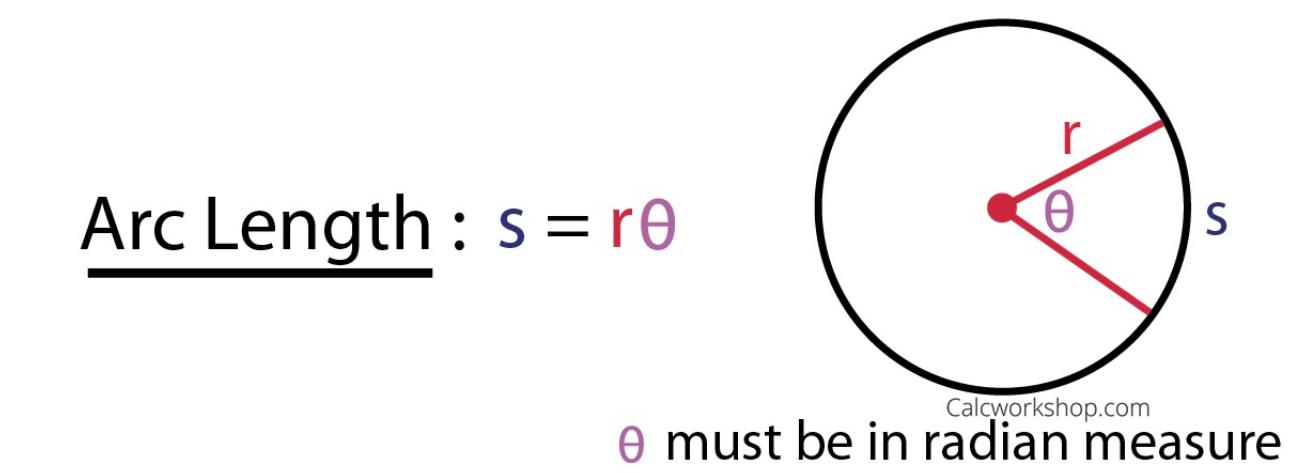
Radius

The distance from the center of the circle to any point on its circumference

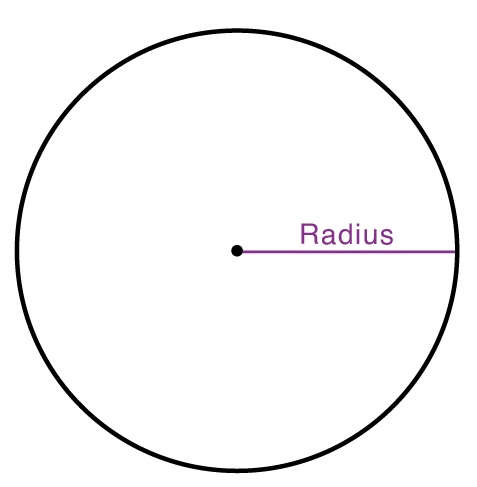
Diamater

The longest distance across the circle, passing through the center also equal to twice the radius

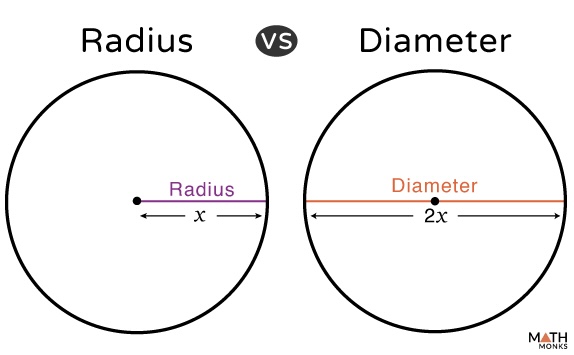
center of a circle

a fixed point that is equidistant from all points on the circumference of the circle.

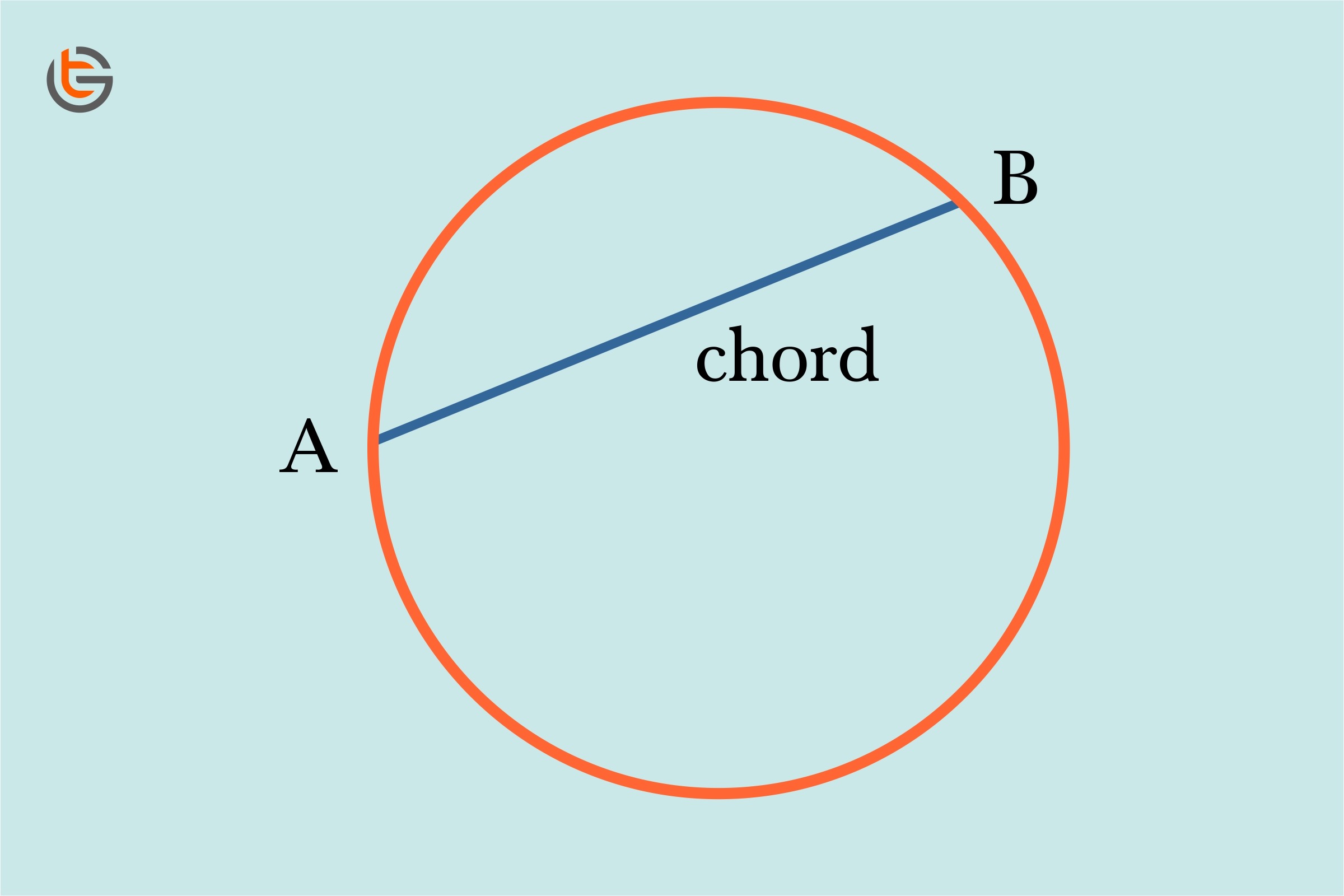
chord

A segment whose endpoints lie on the circumference of the circle.

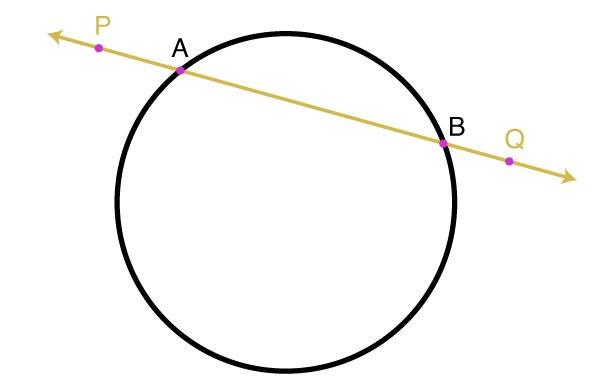
Secant line

A line that intersects a circle at two points, extending infinitely in both directions.

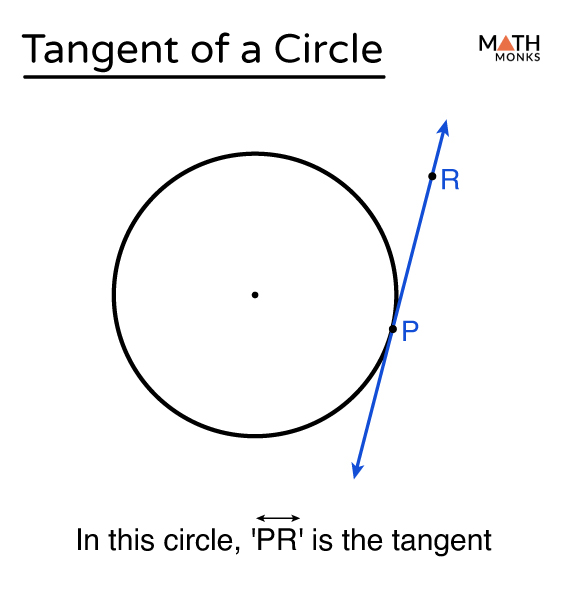
Tangent line

A line that touches a circle at exactly one point, without crossing it.

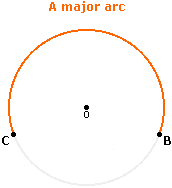
Major arc

An arc that spans more than half of the circle

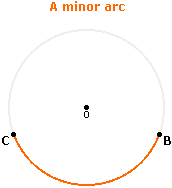
Minor arc

An arc that spans less than half of the circle

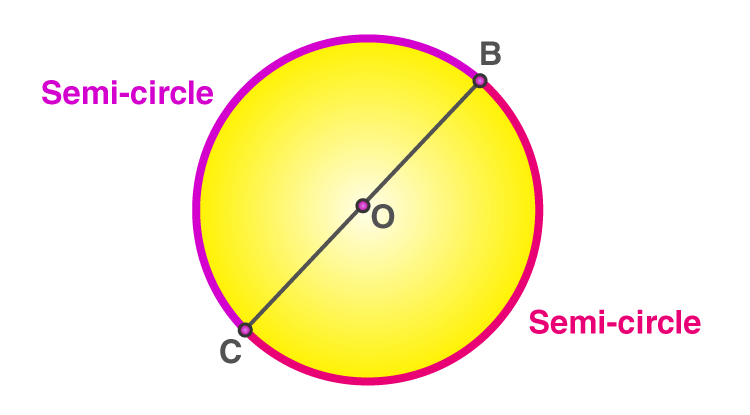
semicircle

An arc that spans exactly half of the circle

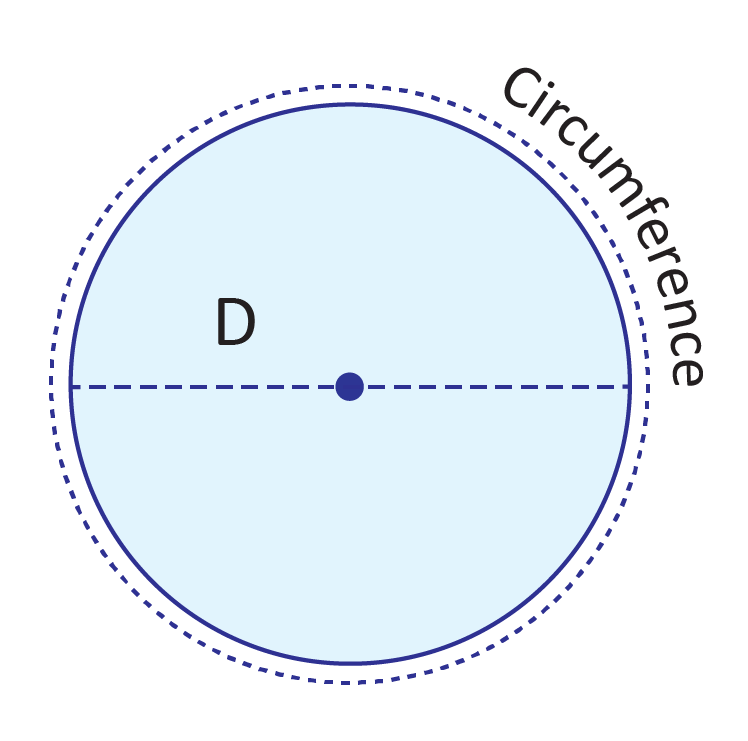
circumference

The total distance around the circle. It can be calculated using the formula C = 2πr, where r is the radius or c= πd, where d is diameter

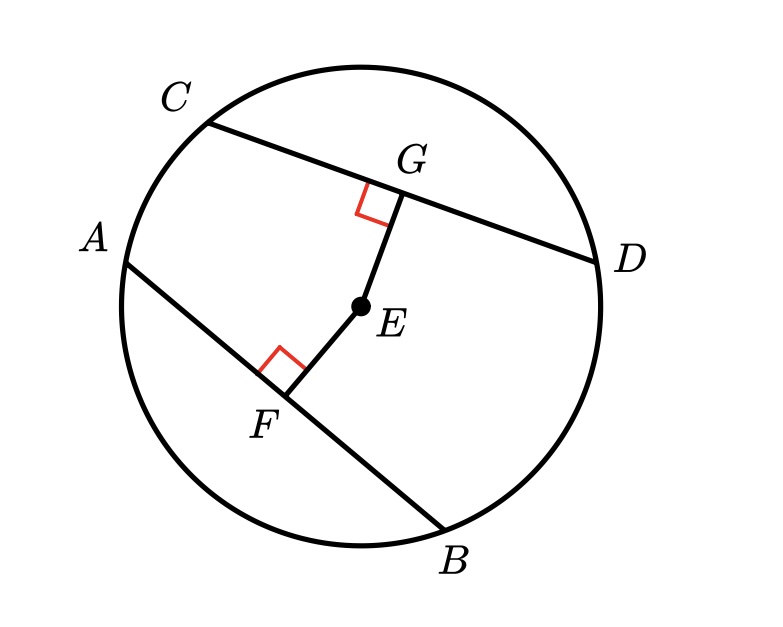
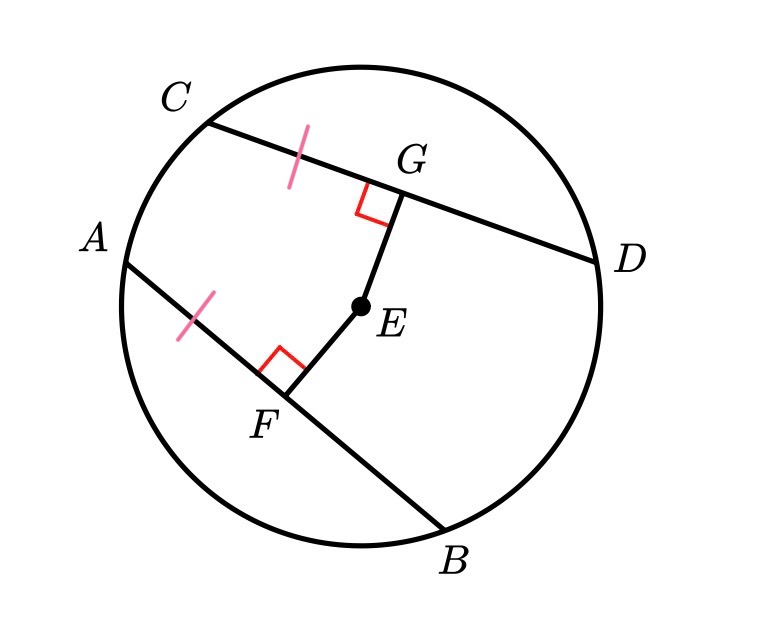
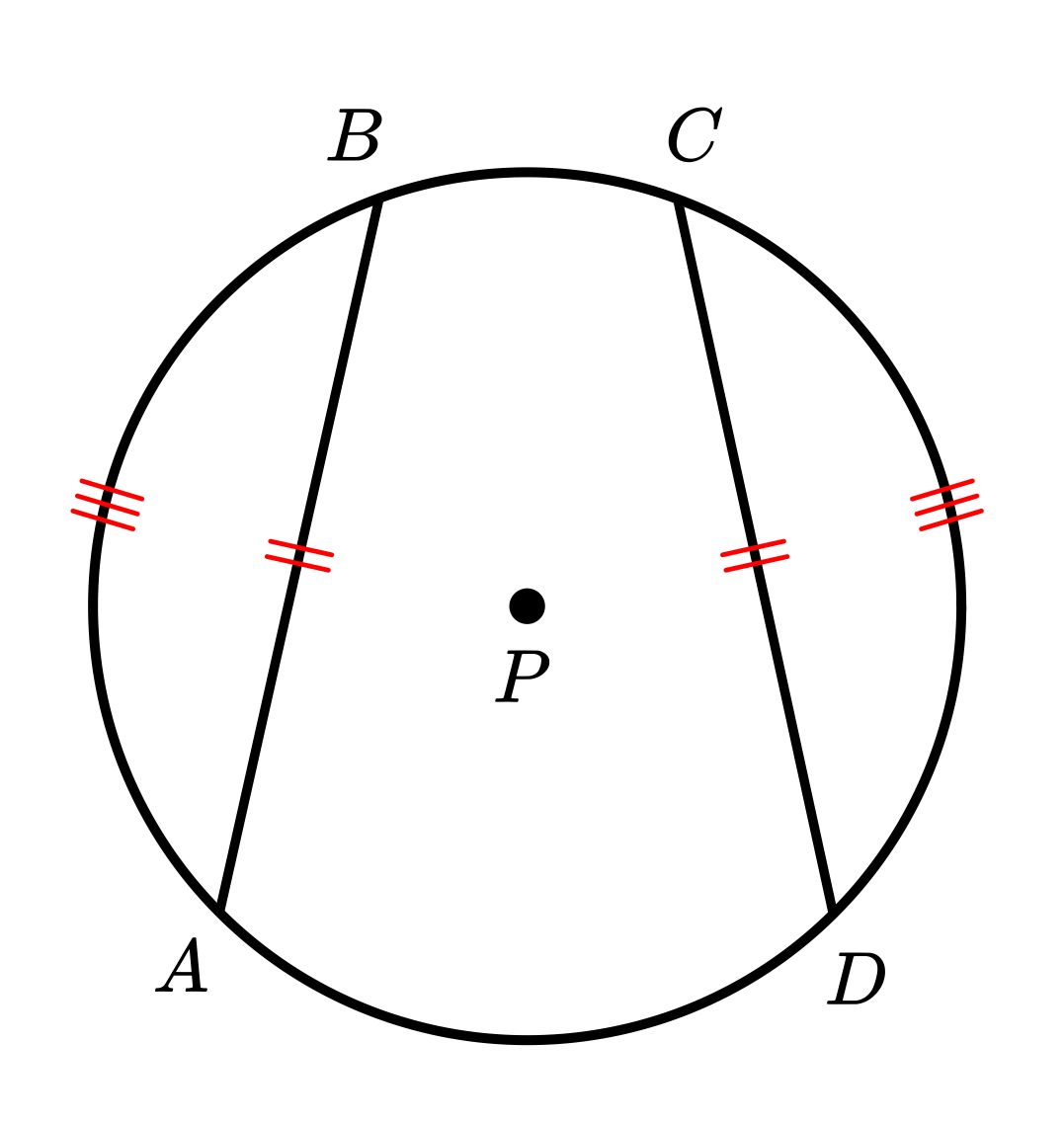
If two chords are equidistant from the center then…

they are congruent

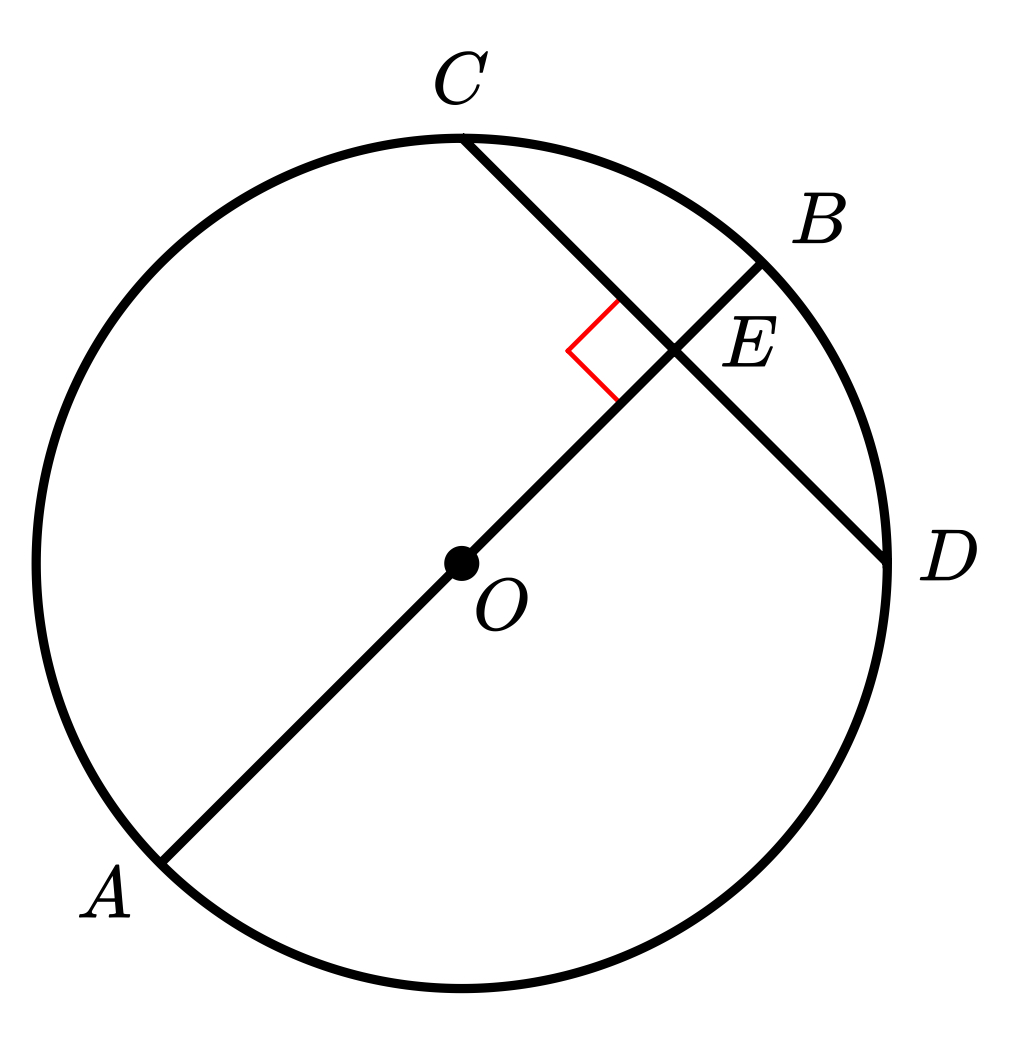
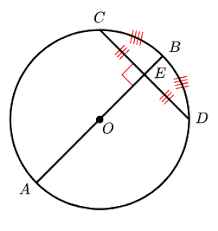
If a diameter of a circle is perpendicular to a chord then..

the diameter bisects the chord and its arc

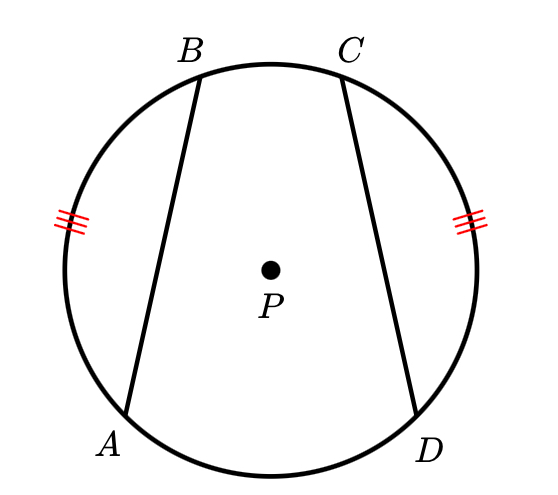
If two chords are congruent then their arcs are…

congruent

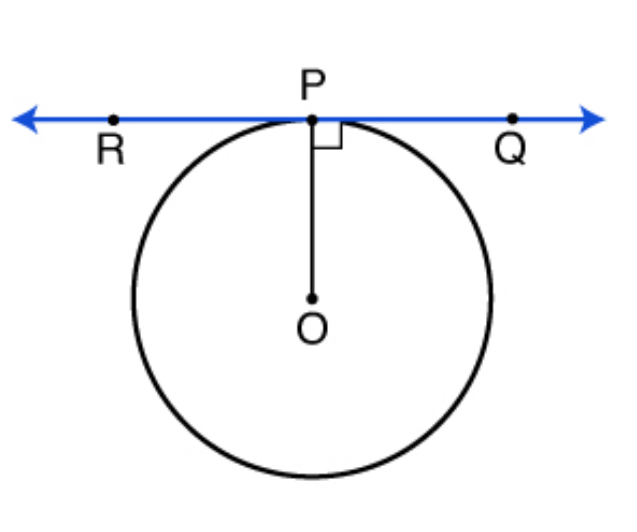
If a line is tangent to a circle then its tangent line is..

perpendicular to the radius at the point of tangency.

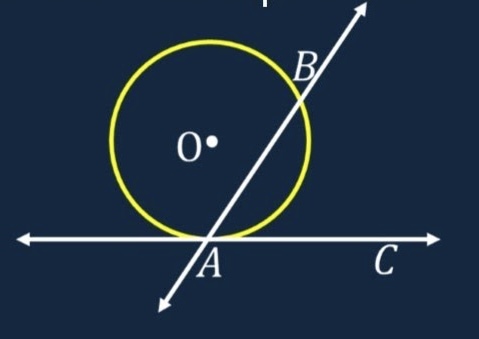
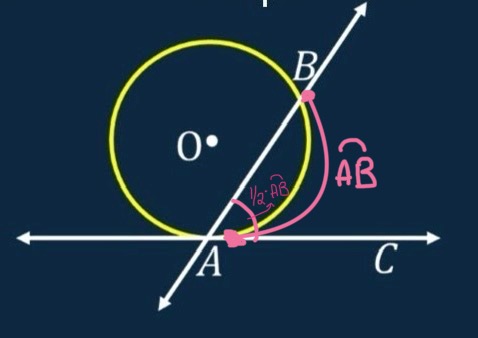
If a tangent and secant line intersects at a point on a circle, then the measure of each angle formed is

half the measure of the intercepted arc

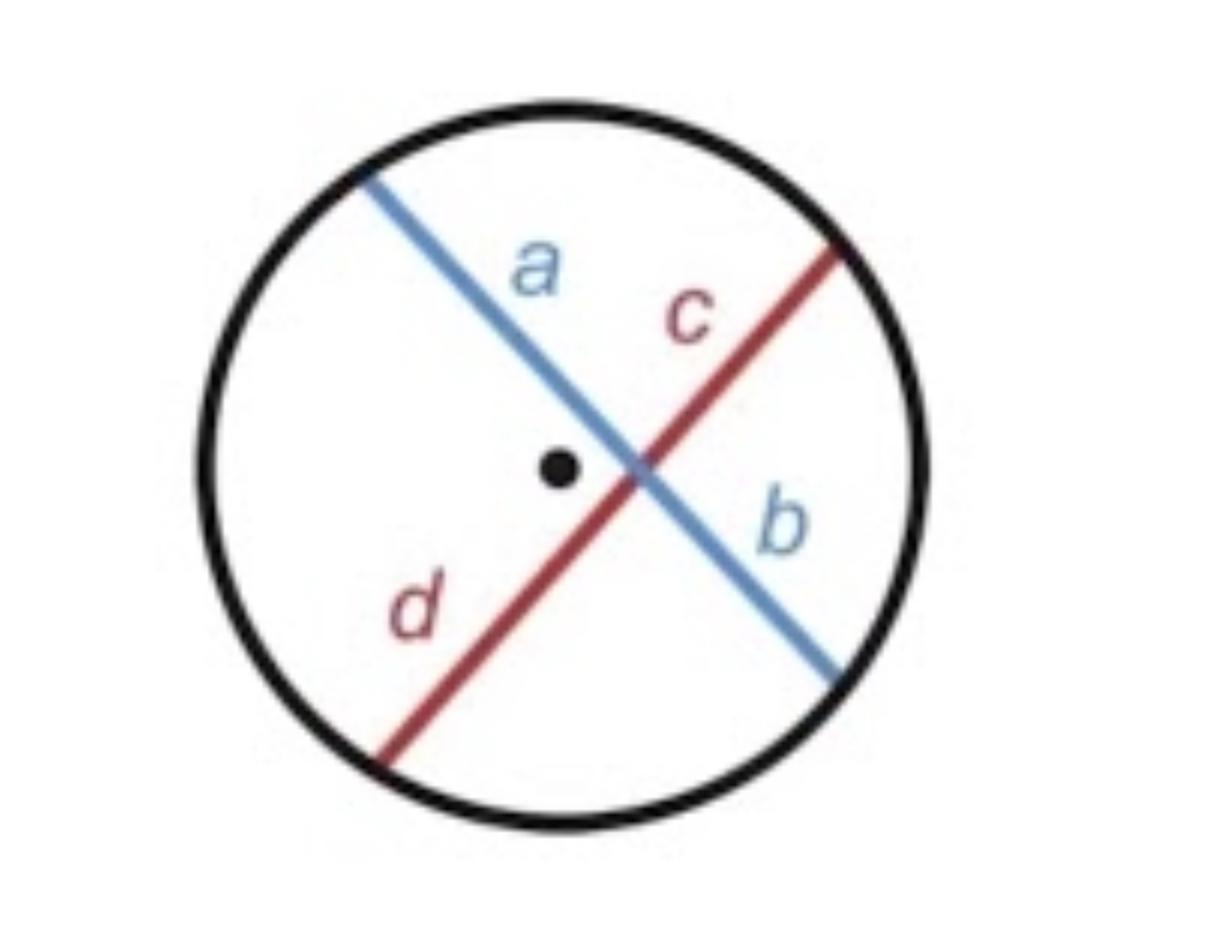
If two chords intersect in the interior of the circle then…

the measure of each angle formed is half the sum of the measures of the intercepted arcs

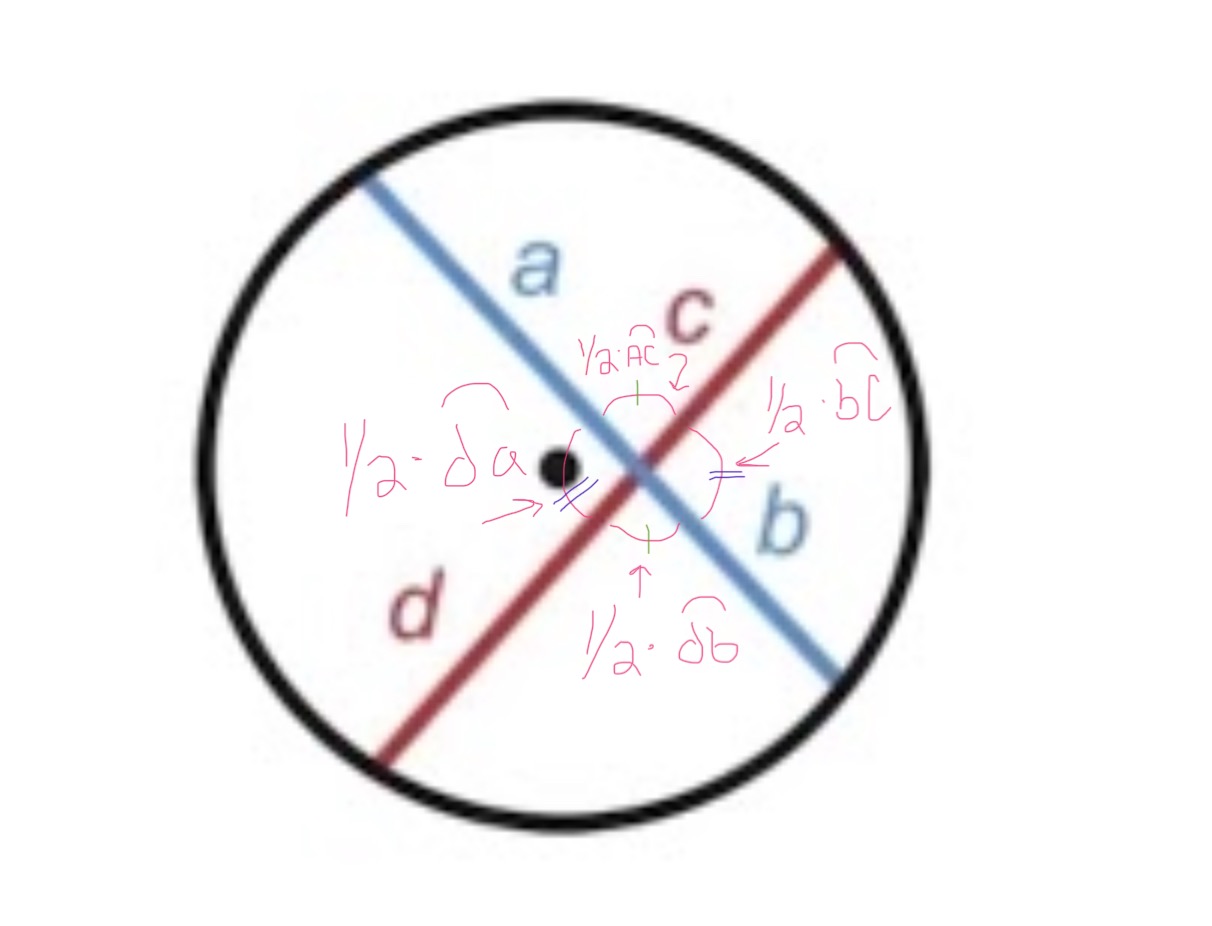
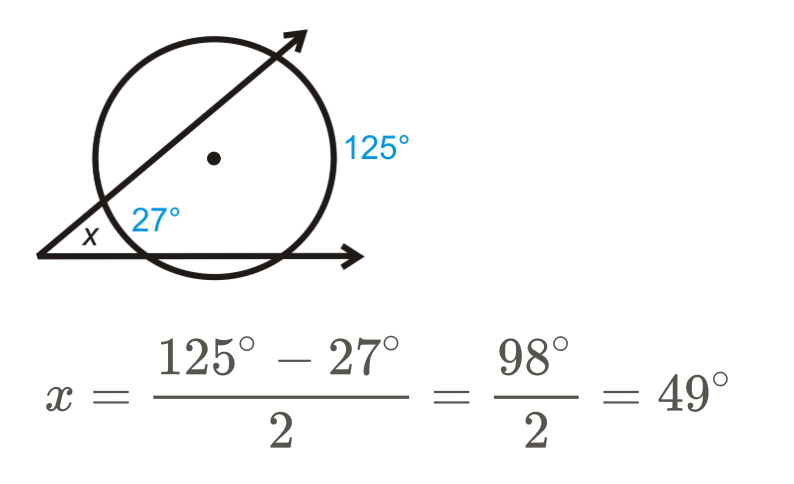
If a tangent/secant, two secants or two tangents create an exterior angle then that angle is …

half the difference of the measures of the intercepted arcs.

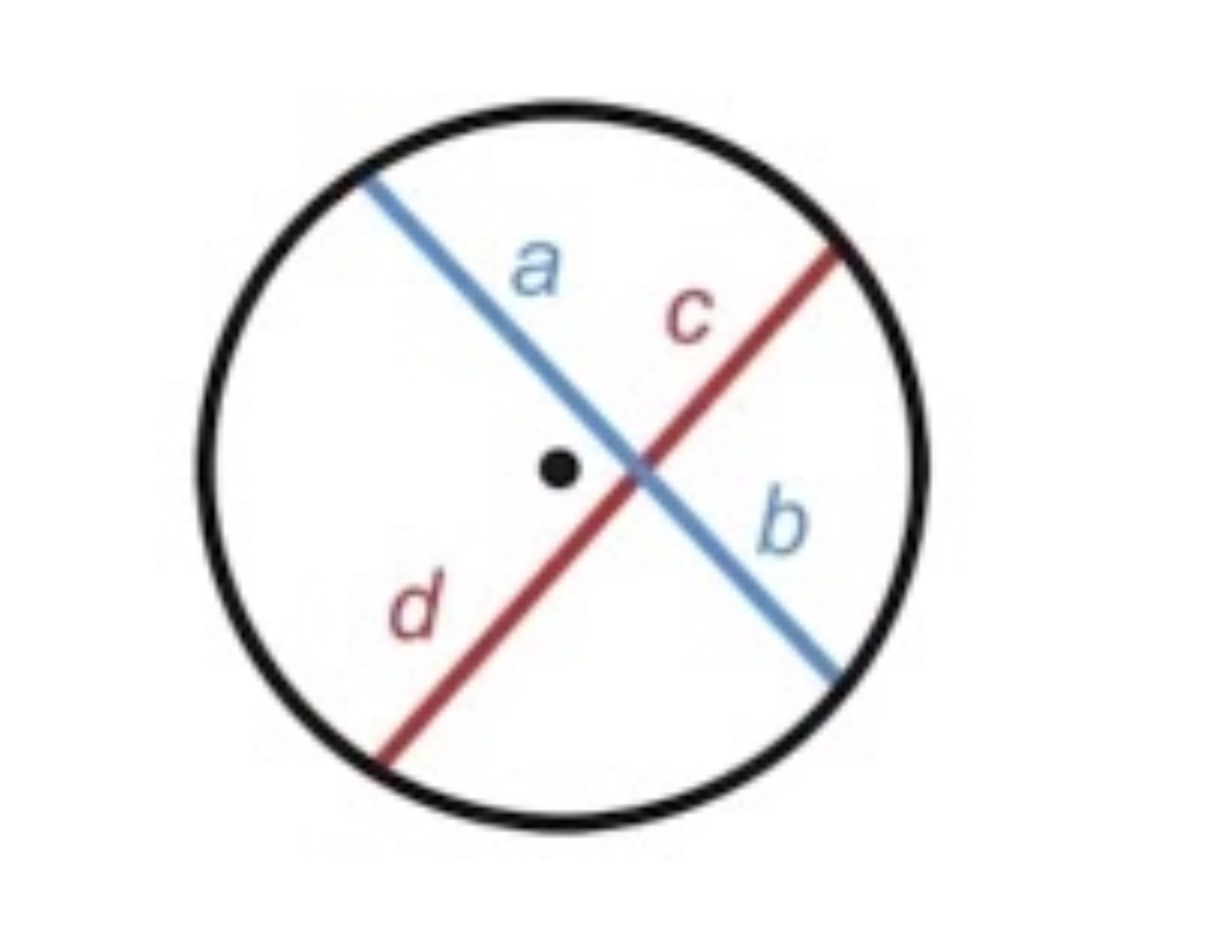
If two chords intersect in the interior of a circle then the…

product of the parts of one chord equal the product of the parts of the second chord.

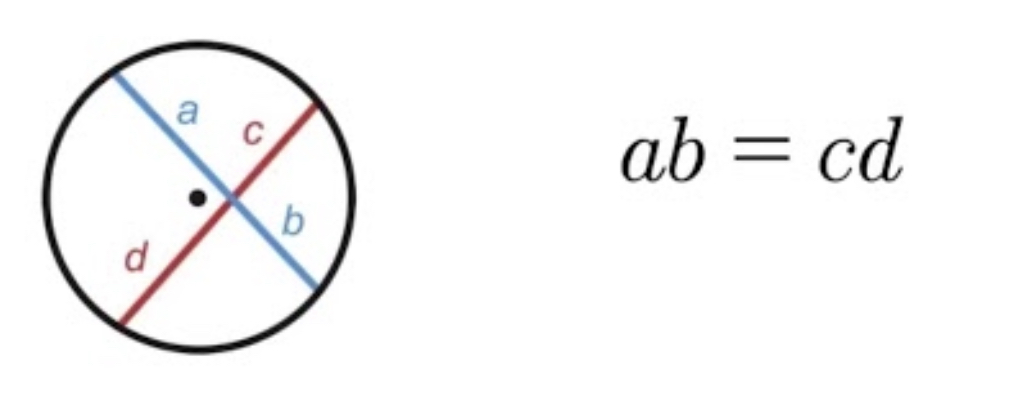
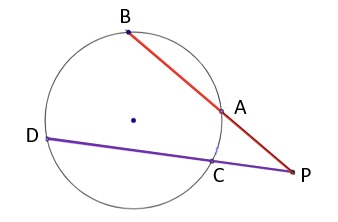
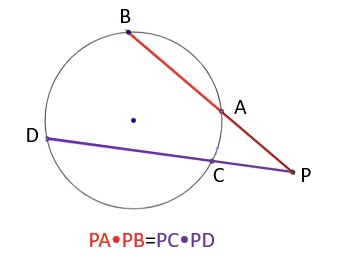
If two secants share the same external point then..

the product of the lengths of one secant and its external segment equals the product of the lengths of the other secant and its external segment.

Equation of a circle

(x-h)² + (y-k)² = r²

Center = (h,k)

Radius = r

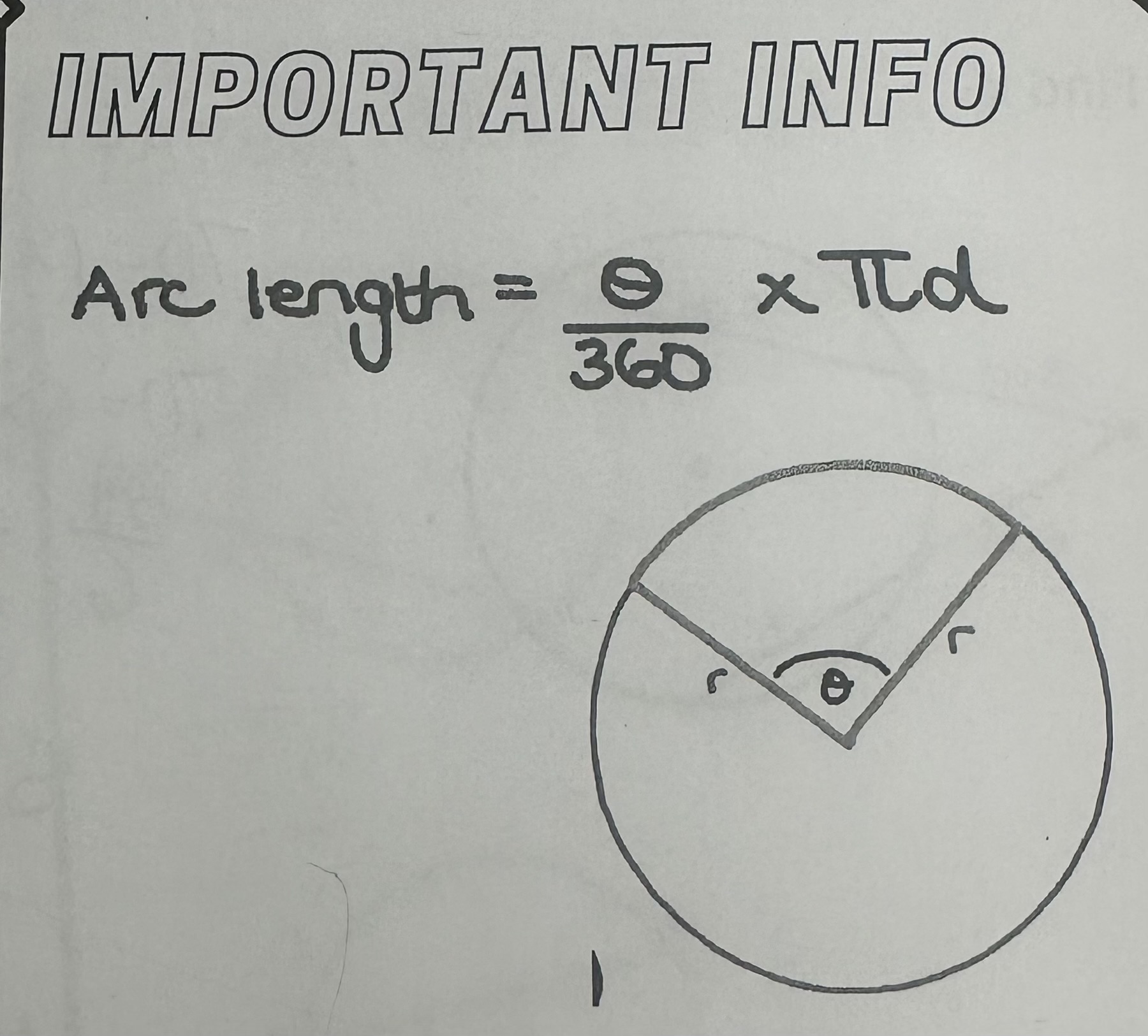
Arc Length equation USING PI

Arc length = θ/360 * πd