AP Calculus AB/BC TTKs

continuity criteria at x = c

• both one-sided limits must exist and be equal at x = c

• f(c) must equal the limit as x approaches c

removable discontinuity (hole)

limit exists at x = c, not equal to f(c)

jump discontinuity

both one sided limits exist, not equal

infinite discontinuity

• at least one of the one-sided limits approaches infinity as x approaches c

• VERTICAL ASYMPTOTE

limit of a constant

constant

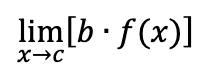
limit of a constant times a function

move constant to outside limit

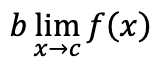
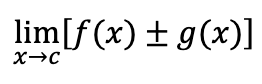
limit of two added/subtracted functions

separate limits and add

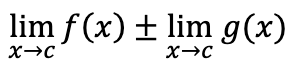
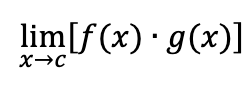
limit of two multiplied functions

separate limits and multiply

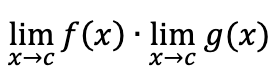
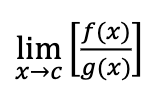
limit of two divided functions

separate limits and divide

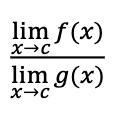
limit = constant/0

limit approaches infinity

limit = constant/approaching infinity

limit approaches 0

limit as x approaches ±∞ = c

y = c is a HORIZONTAL ASYMPTOTE (function can have max of 2)

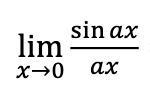
1

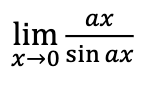
1

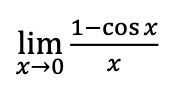
0

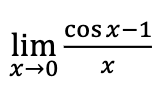
0

If f(x) is continuous on [a,b]…

f takes on every value between f(a) and f(b) INTERMEDIATE VALUE THEOREM

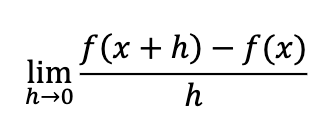
limit definition of a derivative at any point

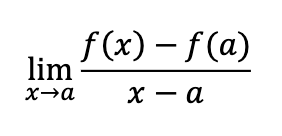
limit definition of a derivative at x = a

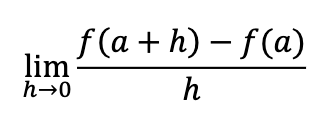
another limit definition of a derivative at x = a

normal line

perpendicular to tangent line

differentiability implies…

continuity

horizontal tangents

numerator of derivative = 0

vertical tangents

denominator of derivative = 0

first derivative test

• changes signs + to - at x = c → relative max

• changes signs - to + at x = c → relative min

• x = c is a critical point where f’ is either 0 or undefined

a function is increasing when…

f’ > 0

a function is decreasing when…

f’ < 0

f” > 0

f’ is increasing and f is concave up

f” < 0

f’ is decreasing and f is concave down

point of inflection at x = c

f” changes sign at x = c

2nd derivative test for relative MINIMUM

f’(c) = 0 and f”(c) > 0

2nd derivative test for relative MAXIMUM

f’(c) = 0 and f”(c) < 0

Product Rule

Used to find the derivative of the product of two functions. If u and v are functions, then the derivative is given by: (uv)' = u'v + uv'

Quotient Rule

low d high - high d low all over low squared