Effect size and Power - L9

Significance testing - levels of significance - look at image

p value is the likelihood of us

observing a trend in the sample (H1) If there is not a trend in the population (H0)

significance level is also the proxy of

Committing a type 1 error

Is a significant results really meaningful?

With a sufficiently larger sample, a statistical test will almost always return a sig result

Significant result doesn’t mean a

meaningful result

We can use effect size to see if the significant results is..

meaningful

Effect size is a measure of the

magnitude/strength of a difference or relationship

effect size is

independent of sample size

Effect size helps its to quantify

practical significance e.g. the importance - can be compared across studies

Common effect size measures

Cohens d (t test)
Partial eta squared for anovas

Pearsons r (correlations)
Cramer’s V for chi squared

cohens d

• measure of effect when we compare 2 groups (t tests)

Cohens d - interpretation

small - less than 0.2

Medium - 0.5

Large - 0.8

Partial eta squared

measure of effect sizes for anova - proportion of variance explained

eta squared intepretation:

0.01 = small effect

0.06 - med

0.13 - large effect

Sample size and effect size - when should we stop testing - before we have collected all the data

• Resource constraints e.g. limited time/money

• Sample size of previous research

• Central limit theorem -

• A priori power analysis

• A priori power analysis -

• work out how many p’s are needed to reliably detect an effect of a certain sample size or larger

Central limit theorem

• distribution of sample becomes more normal as sample gets bigger. More than 30 = sufficient

Decision Errors - 4 types of decisions we can make

• Acccpt Null and no effect in real world - correct d

• Accept alternative H and there is a real world effect - correct d

• Accept Hl and there’s no real world effect - Type I error

• Accept null and theres a real world effect - Type II error

alpha level is

the probability of making a type I error (set at 0.05)

Beta level is the probability of making a

Type II error - usually set at (0.2)

Look at image - displaying that alpha and beta levels -

Power = 1 - beta

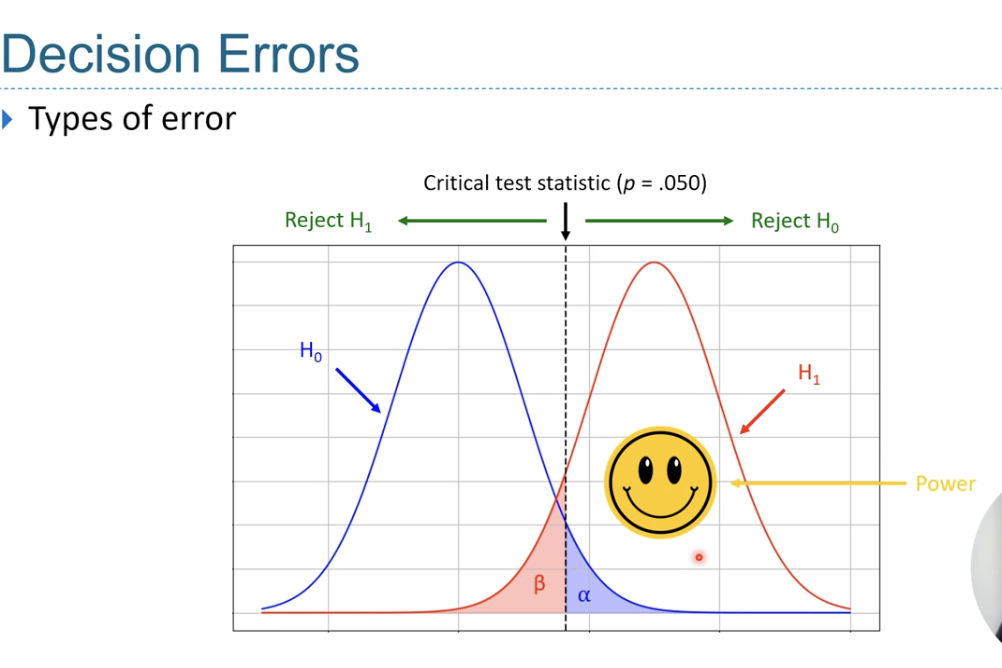
Power

the ability to detect a sig effect if H1 is true

power equation

1 - beta

If beta is set at 0.20 then

power will be 0.8 (80%)

• if there is a genuine effect, there is a 20% chance of failing to reject H0, and 80% chance to successfully reject H0.

Power helps us make sense of

results that are not significant or results that are statistically significnat but not practically significant

Power depends on 3 parameters

alpha level - always set at 0.50

Effect size - larger the effect, the more likely that the effect will be detected - more power

Sample size - larger the more likely the effect will be detected = more power

The more lenient the alpha level, the more

statistical power the test would have

beta increases when the effect is

small , meaning a decrease in power. Larger effect size = higher the power

the larger the sample size the more

power

How to increase power: significance level

set a less stringent sig level (not normally done in psych) or consider a 1 tailed test ( but this should be based on prev research)

How to increase power: increase effect size

by increasing the predicted difference between the population means (using more explicit instructions in the experiment/give more practice time)

• or, decrease population standard deviation (use more controlled environment e.g. lab study rather than natural observation, clear procedure)

How to increase power: increase sample size

recuit more participants

Power analysis with the 4 parameters (Power, sig level, effect size and sample size) we can

given any 3 estimate the 4th - we often don’t have power (use post hoc power analysis)

Power analysis p- we can also determine the sample size to achieve certain level of power (0.8) with

a specific effect size and significance level - A priori power analysis

Post hoc power analysis ….. we can look at whether a non - sig test result is

likely to be due to a lack of power

• post hoc because it is concrete after data collection

A priori power analysis - determine the required..

sample size before conducting the test

• A priori - as it is conducted before data collection - we need the other 3 parameters

Effect size for A priori power analysis

• This is the size of the effect that you would like to be able to reliably detect

Effect size for A priori power analysis - determine via Previous/ pilot study but…

• exact effect size from a pervious/ pilot study

• Assumes the conditions to be similar enough to your study

Effect size for A priori power analysis - determine via general bench marks

• effect size benchmarks (e.g. small, med, large)

• Helpful when previous studies do not provide a consistent effect size - but less precise