Calc AB Unit 1 Limits

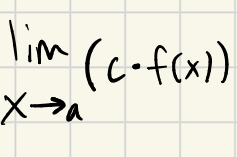
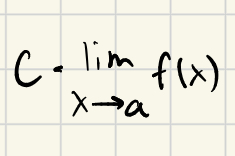
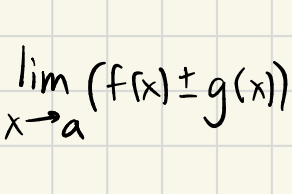
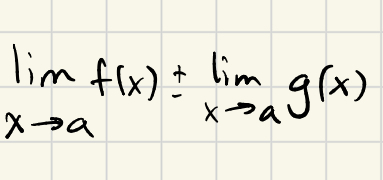
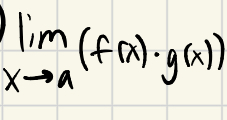
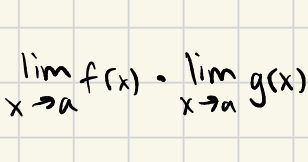
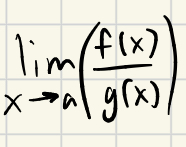
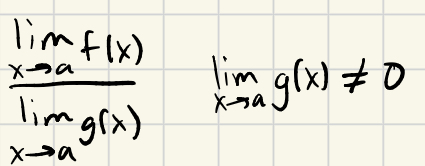
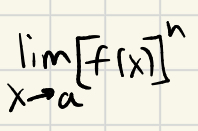
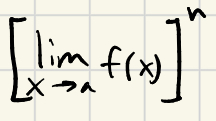
What does lim_x→ac equal?

c

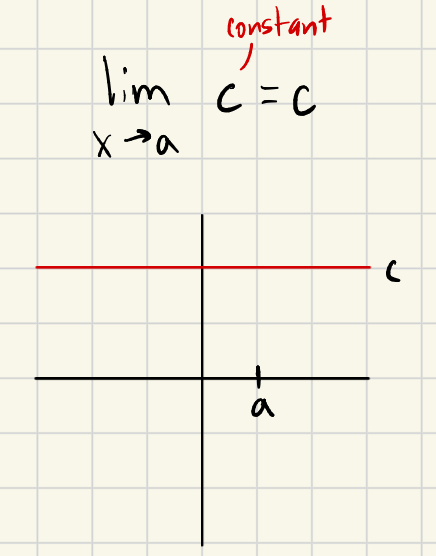
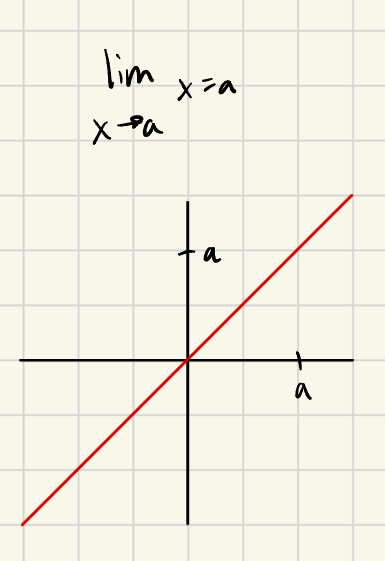
What does lim_x→ax equal?

a

When does lim_x→af(x) = f(a)

When there are no asymptotes

Denominator doesn’t equal 0

What is indeterminate form

f(a)/g(a) = 0/0

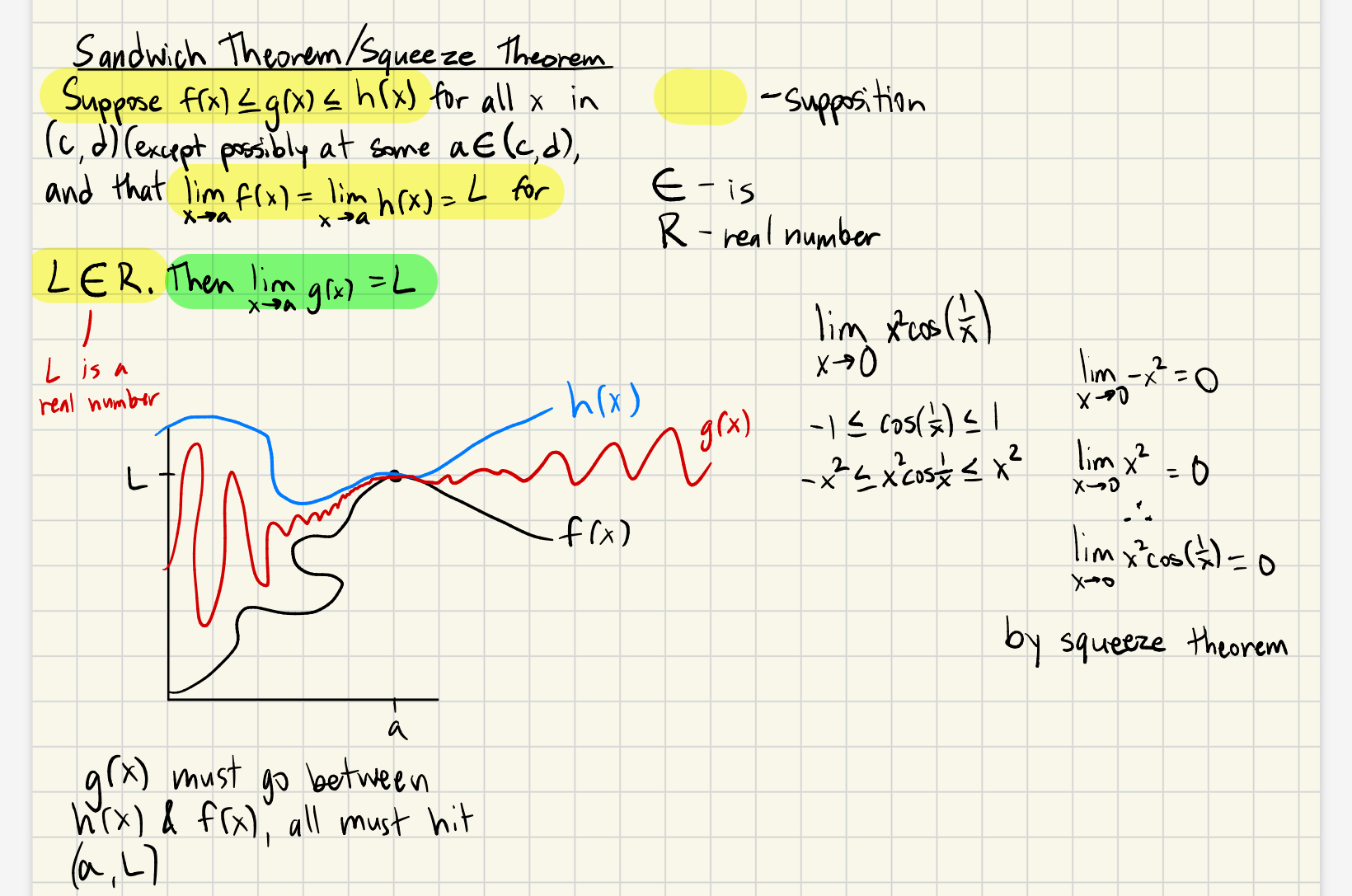
Squeeze/sandwich theorem

Suppose f(x)≤g(x)≤h(x)

And lim_x→af(x) = lim_x→ah(x) = L

Then lim_x→ag(x) = L

Continuous function rules

1. f(a) must be defined

   every x value must have a y value

2. lim_x→af(x) must exist

   overall limit

3. lim_x→af(x) = f(a)

   lim must be at func value

Intermediate value theorem

Suppose f(x) is continuous on [a,b]

And W is a number between f(a) & f(b)

Then a number c is between [a,b] where f(c) = W

If f(x) decreases without bound as x→ a, then what does lim_x→af(x) equal

-∞

If f(x) increases without bound as x→ a, then what does lim_x→af(x) equal

∞

How to know if there is an infinite limit vertical asymptote

vertical asymptote: lim_x→af(x) = (b/0) = ±∞

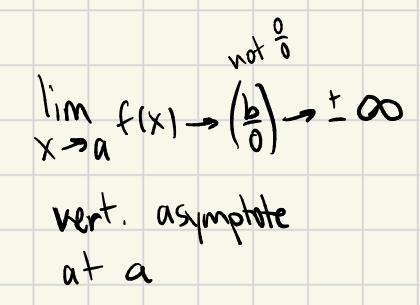
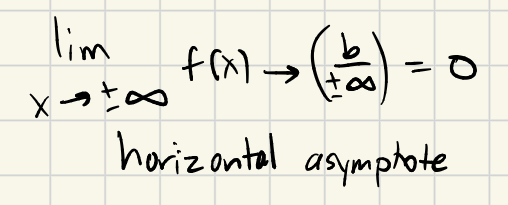
How to know if there is an infinite limit horizontal asymptote

horizontal asymptote: lim_x→±∞f(x) = (b/±∞) = 0

If f(x) approaches L as x gets very large/small, then…

Large: lim_x→∞f(x) = L

Small: lim_x→-∞f(x) = L

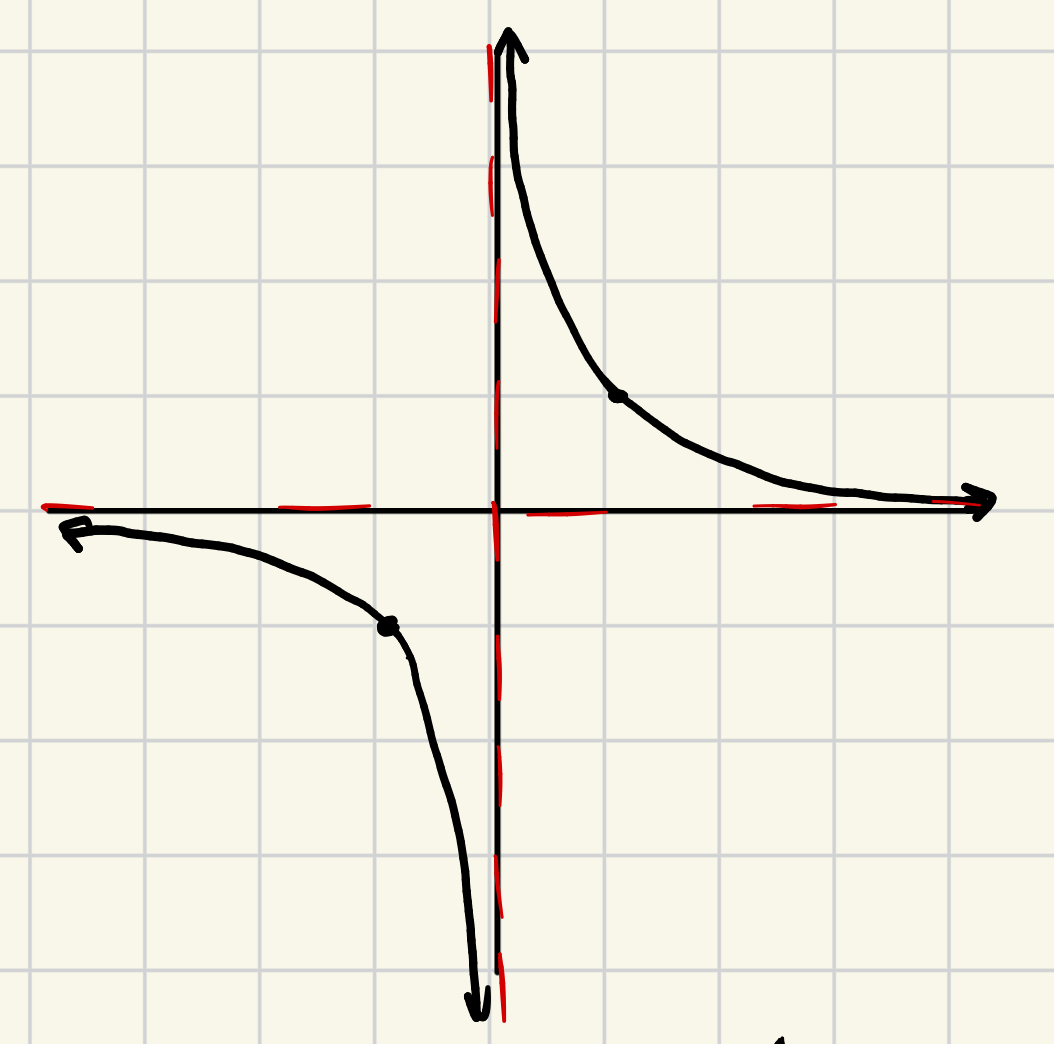
^{lim_x→∞(1/x)=}

^{lim_x→-∞(1/x)=}

0

0

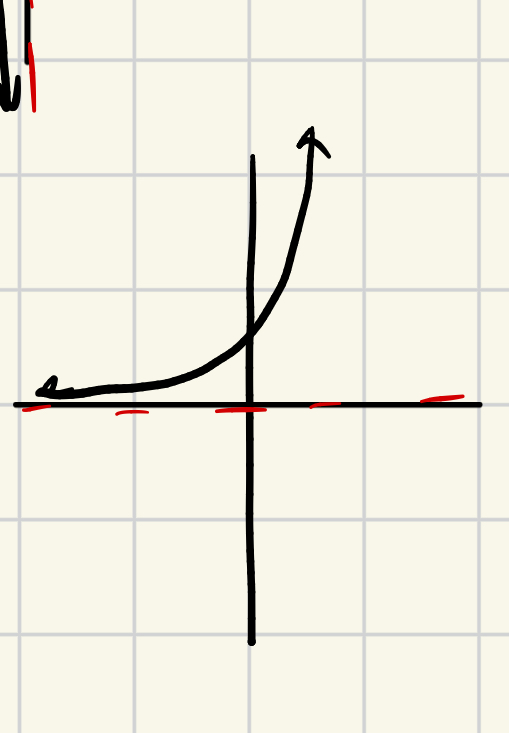
lim_x→∞(e^x)=

lim_x→-∞(e^x)=

∞

0

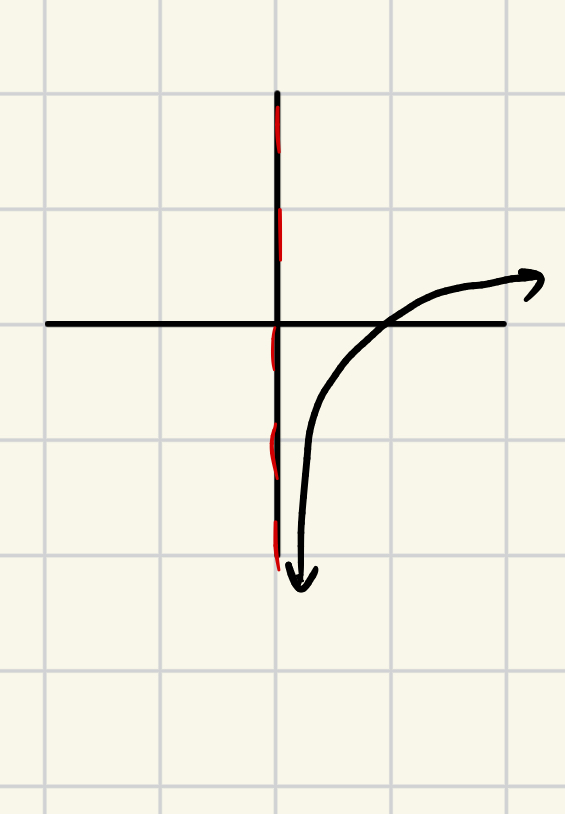
lim_x→0⁺(lnx)=

∞

How to know if a function approaches infinity?

When plugging in a, lim_x→af(x) = b/0

How to tell if discontinuous function approaches positive or negative infinity?

If a number to the left of a makes the limit negative, then it approaches negative infinity

If a number to the right of a makes the limit positive, then it approaches positive infinity

What does it mean if lim_x→af(x) = ∞

There is a vertical asymptote

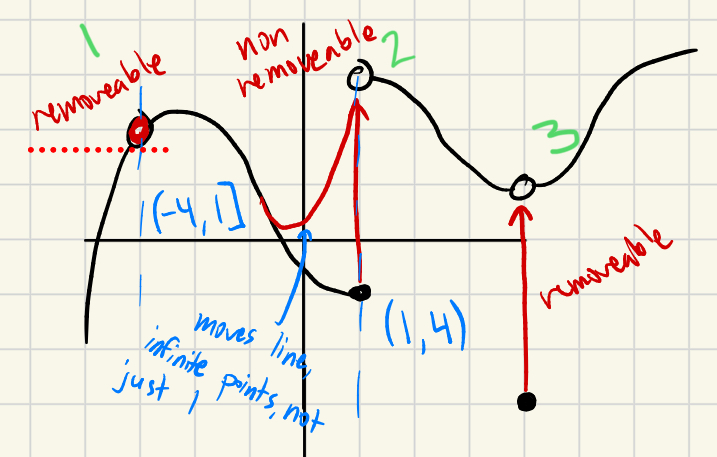
Non-removable discontinuity