5. Quantum Numbers

what do quantum numbers descirb

the e-s in an atom

what are the 2 things the pricniple quantum number deescribes

describes shells or energy levels or orbitals

1. size of a shell

2. E of a shell

ex: for Li, for 2nd shell > it is bigger than n=1 and has more E than n=1

what letter reperesnts the secondary quantum number + 2 other names for it

letter 'l'

angular momentum quantum #

the azimuthal quantum #

what was later discovered abt the emission spectrum and why was this initally missed

discoevered that EACH bright line was actually a SERIES of lines (w slightly diff frequencies therefore slightly diff Energies)

missed at first bcs the lines were so close tgt and couldnt be distinguished when tech was not so advanced

what did the presence fo multiple lines in emission spectrum mean + who theorized

1915, arnold sommerfeld theorized that each main Energy level/shell (n value) consisted of subshells

what does the secondary quantum # (l) describe + what range does its values have

l describes the SHAPE of each SUBSHELL

- the # of subshells in a shell range from 0 to n-1

ie) if n=3, number of subshells: 0,1,2 so 3 subshells

how are the subshells (l) numbered + lettered and each general shape

l = 0 = s (sharp)

l = 1 = p (principle)

l = 2 = d (diffuse)

l = 3 = f (fundamental)

s > sphere

p > dumbbell

d > 4 clover leaf

f > bunch of eggs *dont need to know

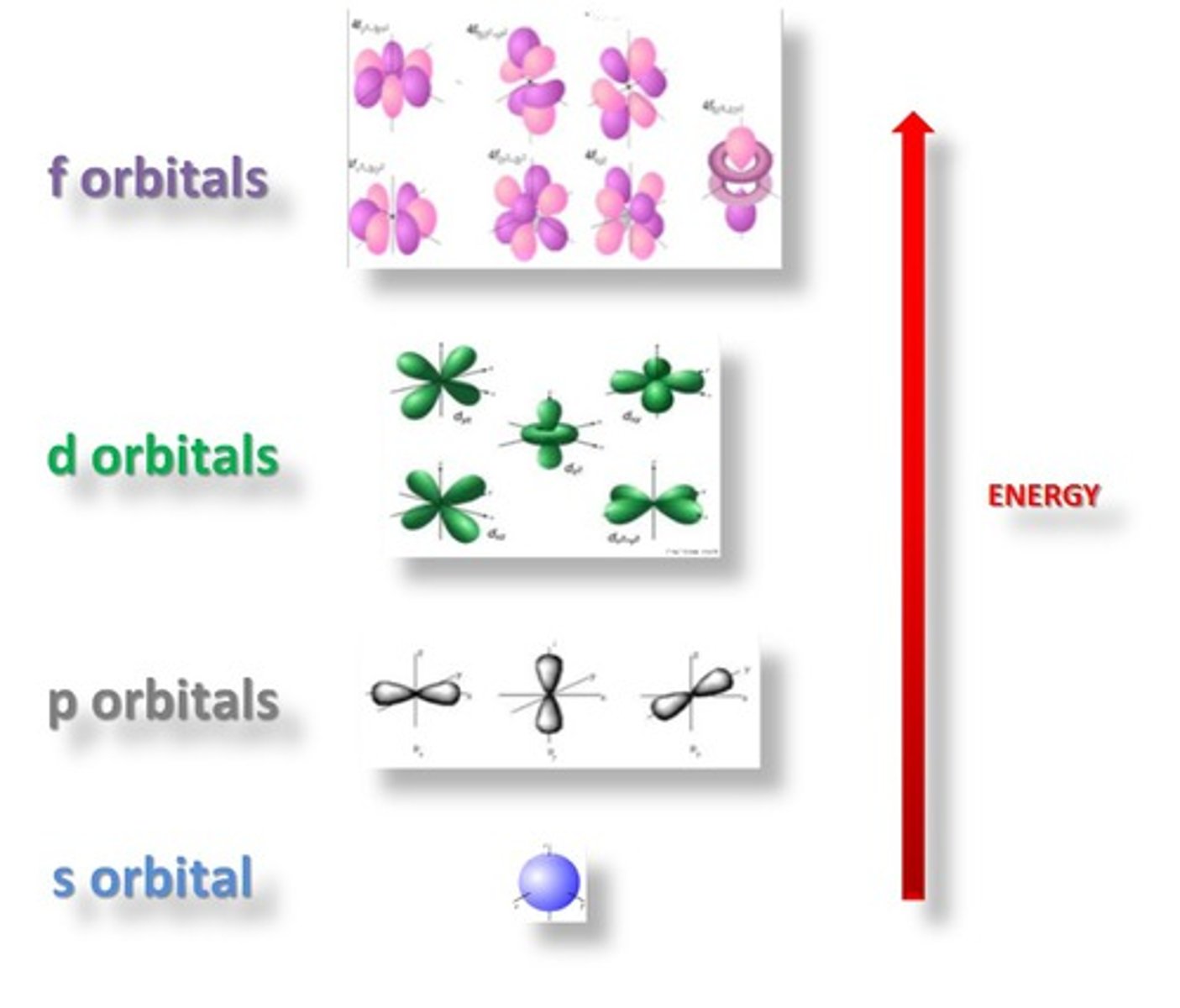
how to know how mnahy subshells each shell/orbital will have

for each shell, there are 'n' kinds of subshells

so if n=3, 3 diff types of subshells (s, p, d corresponfing to 0, 1, 2)

what is m(subscript l)? and what it describes

mₗ = magnetic quantum number

sommerfeld explained that the diff shaped subshells could exist in diff positions of orientations > known as suborbitals

> magnetic quantum # describes the orientation of one suborbital, relative to another

what is the range for the values of mₗ aand how does this correspond to the diff orientations for s,p, d, f

range for mₗ = -l to +l where the # of values possible in total correspods to the # of orientations for that subshell)

~ for s: l = 0 so mₗ can only be 0 > only 1 value means only 1 orientation (only 1 way to draw a sphere)

~ for p: l = 1 so mₗ for 1 can be -1,0,1 so 3 values = 3 orientations

~ for d: l= 2 so mₗ for 2 can be -2,-1,0,1,2 so 5 values = 5 orientations

~ for f: l =3 so mₗ for 3 casn be -3, -2, -1, 0, 1, 2, 3 so 7 values = 7 orientations

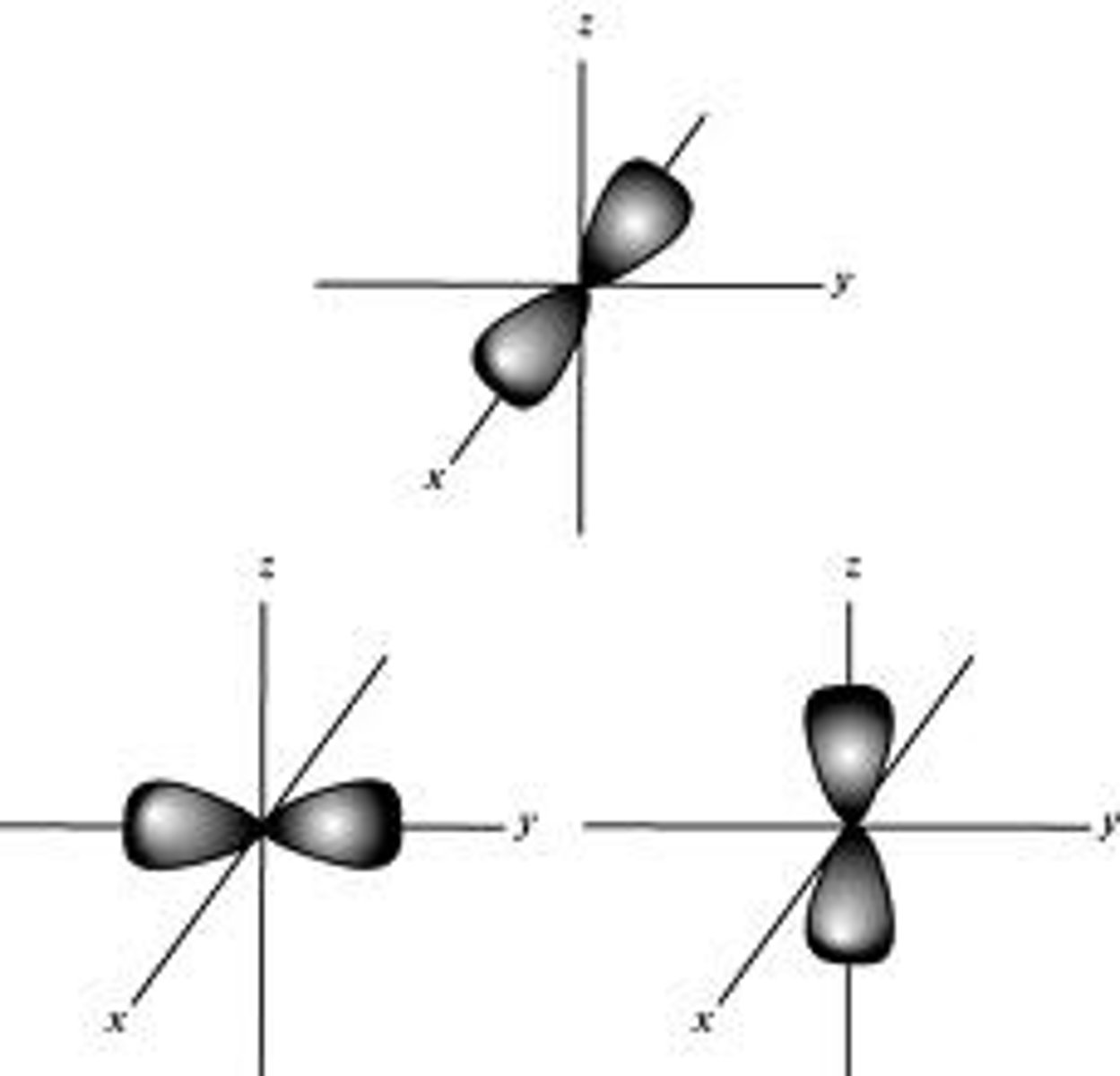
name and draw the 3 orientations for p subshell

(pₓ, pᵧ, pz)

each subscript shows which axes the balloons are aligned on top of

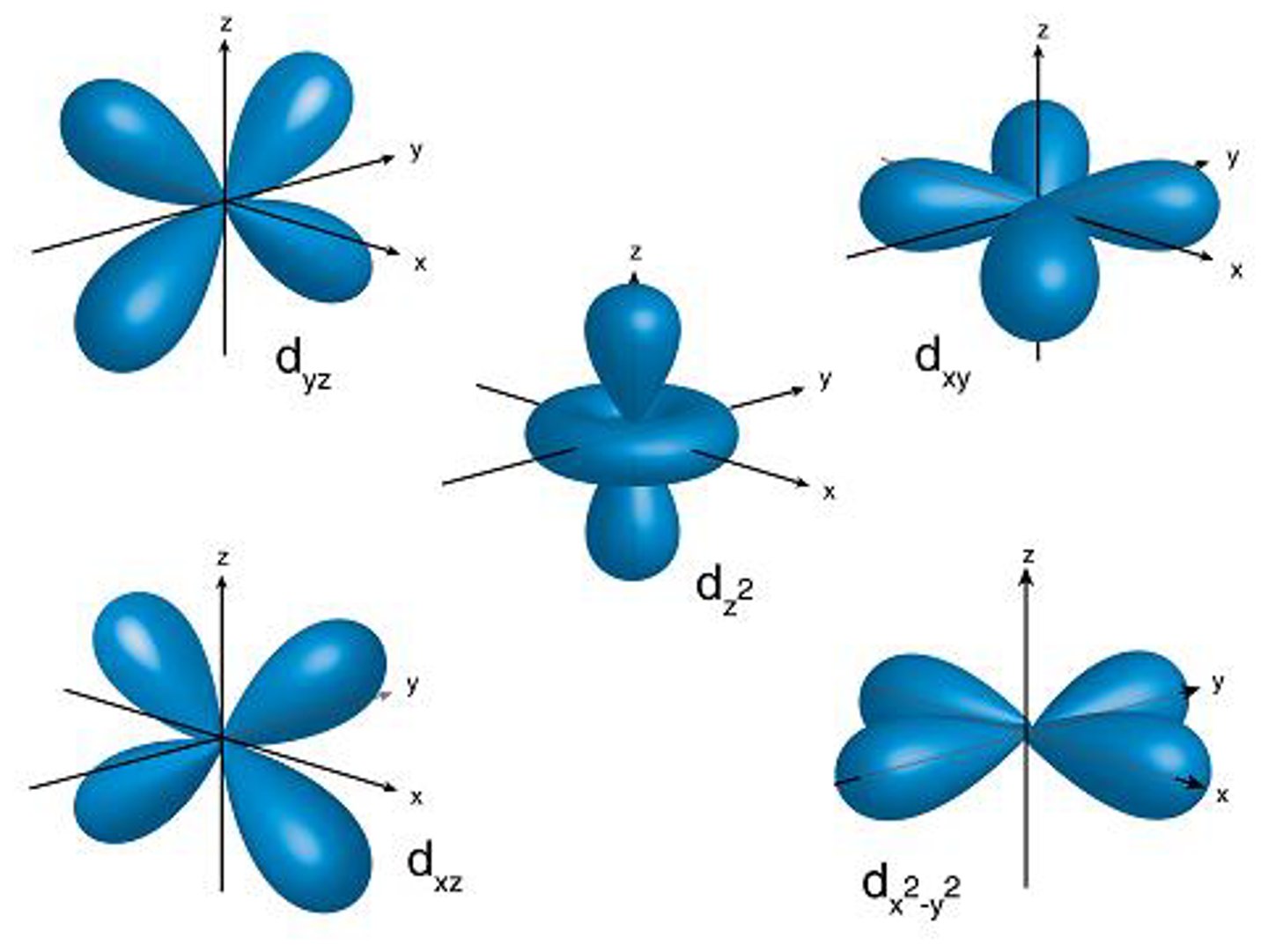
name the 5 orienattaions for d subshell + what each looks like

dₓᵧ

dᵧz

dₓz

dₓ² - ᵧ²

dz² (ring around the middle)

subscripts correspond to the planes where the balloons are in

unless name is squared, the balloons are in the space BETWEEN the 2 axes

if squared, the balloons are ON the axes

formula for the total number of suborbitals in a shell and how many e-s in eah suborbital

n^2 = the total # of suborbitals in a shell (number of values possible for mₗ)

2e-s in each suborbital

what is mₛ

magnetic spin quantum number

if e-s are negative and like charges repel, why do they pair up & who theorized the reasoning

1925, wolfgang pauli theorized that e- are constantly spinning

when they pair up, they rotate with equal magnitude but opposite direction

these opposite spins create oppste electrical force

therefore the attraction of the opp electrical forces is GREATER than the repulsion of the identical charges

Hund's Rule

Hund's rule states that:

Every level in a subshell is singly occupied before any level is doubly occupied.

All of the electrons in singly occupied sublevels have the same spin (to maximize total spin).

aka we fill up sublevels with 1 electron first before doubling them up bcs as the negatively charged electrons fill sublevels, they first try to get as far as possible from each other before having to pair up.

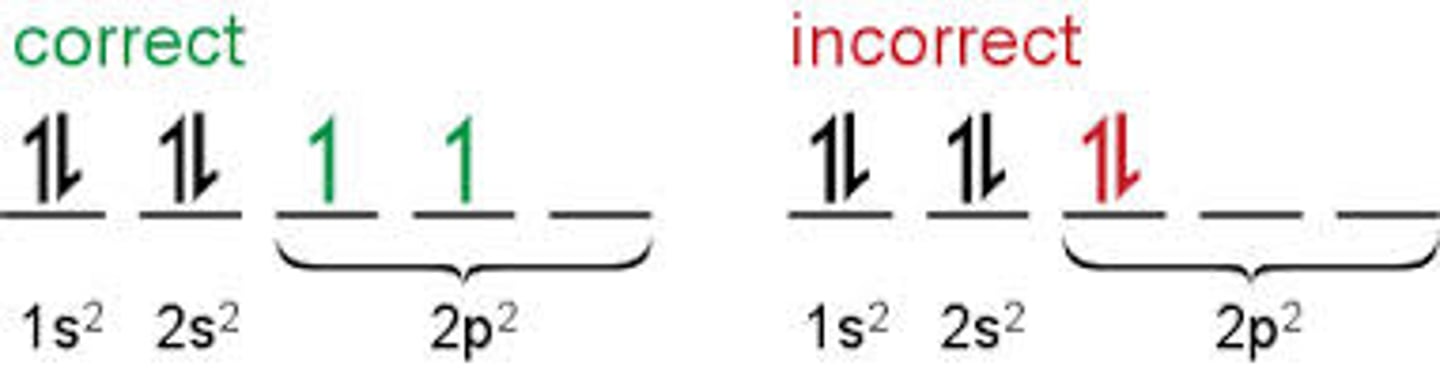
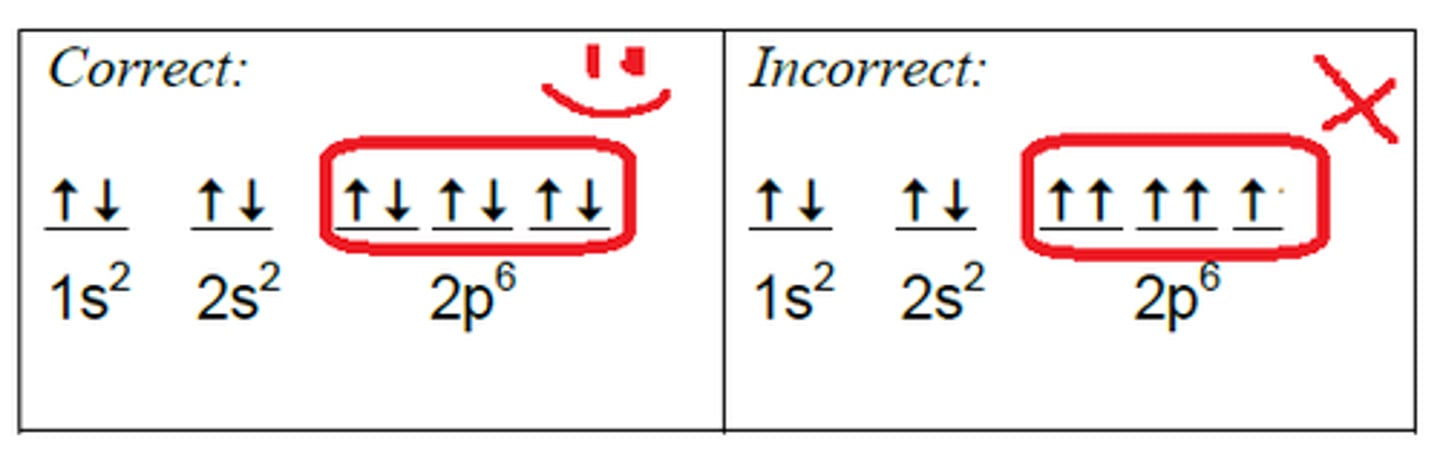
Pauli Exclusion Principle

Pauli Exclusion Principle states that, in an atom or molecule, no two electrons can have the same four electronic quantum numbers.

As an orbital can contain a maximum of only two electrons, the two electrons must have opposing spins. This means if one electron is assigned as a spin up (+1/2) electron, the other electron must be spin-down (-1/2) electron.

understand why pauli exclusion principle must alwasy be true

bcs if 2 e-s had all the same quantum numbers then they would have the same directional electric feild (no opp spin if both are +1/2 etc) so they will both repel eo completely as there is no electric fweild to overpower the repuslion of their negative charges

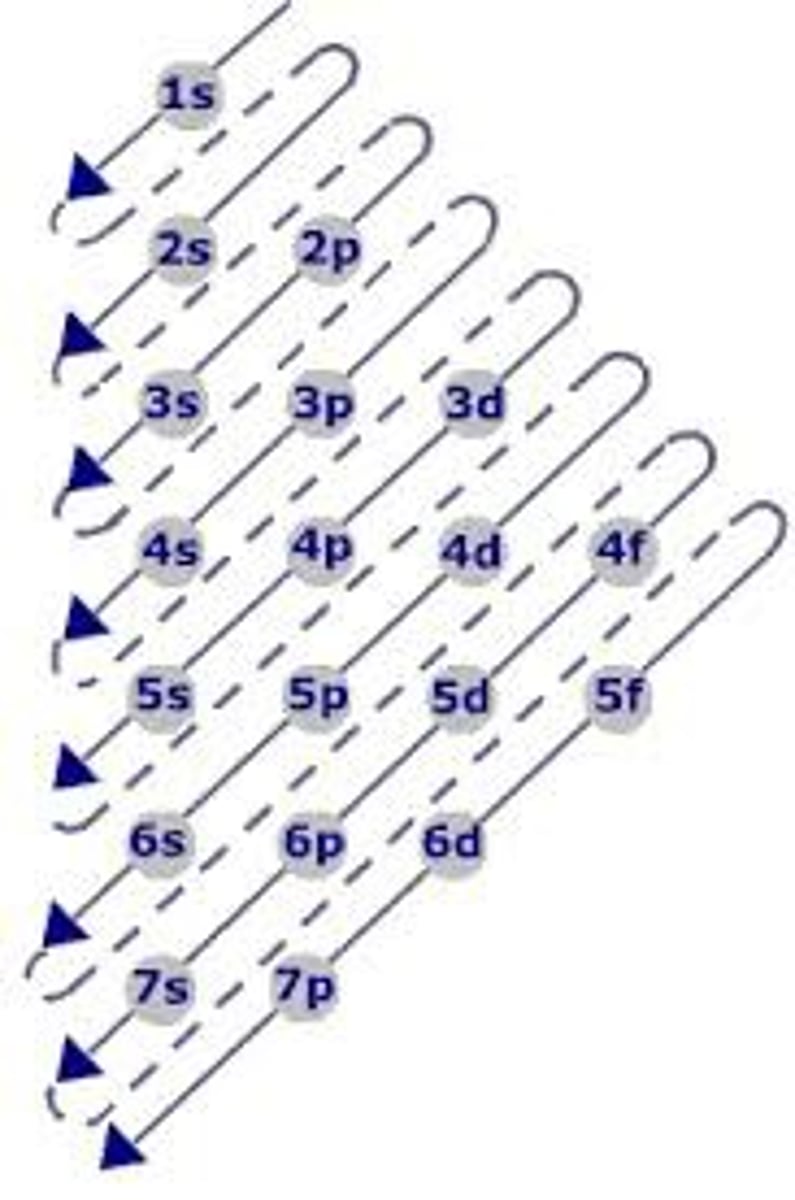
The Aufbau Principle + what visual tool helps follow the principle

The Aufbau principle states that an electron occupies orbitals in order from lowest energy to highest.

- we must fill up e-s in the lower orbitals (n=2) before starting higher orbitals (n=3)

can also use the diagonal rule of electron filling order (in diagram)