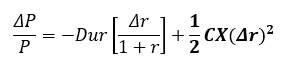Chapter 3 Lecture Notes

1. Interest Rate Measures

1. Coupon Rate

2. Required Rate of Return (r)

3. Expected Rate of Return [E(r)]

4. Required [r] versus Expected [E(r)] Rates of Return

5. Realized Rate of Return

Coupon Rate

the annual dollar coupon divided by the face value.

Example: a $1,000 par-value bond with a 5% paid semiannually.

Coupon payment (every six months)= 0.05 x $1000 / 2= $25.

Required Rate of Return (r)

the annual rate of returns an investor believes they should earn on a bond given the risk level of the investment. This is the rate used by investors to calculate fair present value (PV).

Expected Rate of Return [E(r)]

the rate of return an investor expects to earn when the investor buys the security at its current market price (P), holds it until maturity, and reinvests each coupon payment at the [E(r)].

Required [r] versus Expected [E(r)] Rates of Return

If the security is correctly priced [fair present value (PV)= current market price, (P)], the expected rate of return is the same as the required rate of return, E[r]= r.

For an undervalued security [P<PV], E[r]>r.

For an overvalued security [P>PV], E[r]<r.

Realized Rate of Return

the rate of return actually earned over the investment period.

2. Bond Valuation

The fair present value (PV) of a security is determined using the yield-to-maturity (r) as the discount rate.

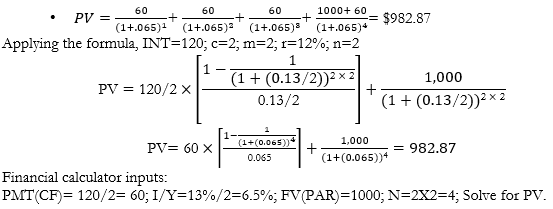
Example

What is the fair present value (PV) of a 2-year, $1000 par value bond; 12% coupon rate paid semiannually; with a required rate of return (r) of 13%?

Coupon payment (CF)=0.12 x 1000 = 120 annually, or 120/2 = $60 semiannually. r=13%/2= 6.5% semiannually. Last (fourth) payment includes principal (1000) + interest (60):

3. Equity Valuation

1. Zero Growth in Dividends

2. Constant Growth in Dividends

Zero Growth in Dividends

The present value of a stock (Pt) assuming zero growth in dividends can be written as:

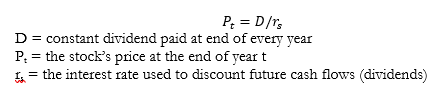
Constant Growth in Dividends

The present value of a stock (Pt), assuming constant growth in dividends, can be written as:

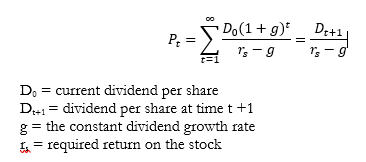
4. Impact of Interest Rate Changes on Security Values

KEY CONCEPT: Inverse relation between interest rates (r) & security prices (P). r, P

In the example above, what is the price of the bond if discount rate increases to 14%?

(i.e., what is the fair present value (PV) of a 2-year, $1000 par value bond; 12% coupon rate paid semiannually; with a required rate of return (r) of 14%?).

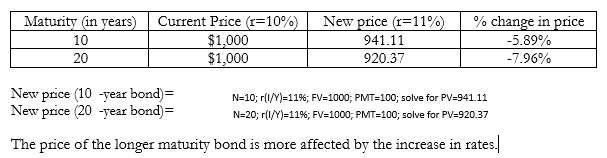
5. Impact of Maturity on Security Values

KEY CONCEPT: Longer maturity securities are more sensitive to changes in interest rates.

Example

Assume the following are $1000 par value bonds with a 10% annual coupon. Current required rate of return is 10%. Bonds have maturities of 10 and 20 years. What is their price if rates increase by 1% to 11%?

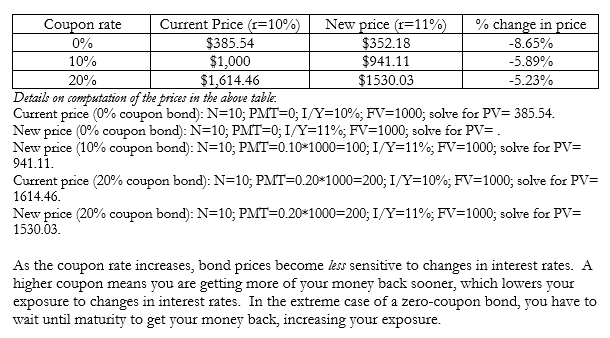
6. Impact of Coupon Rates on Security Values

KEY CONCEPT: Higher coupon rate securities are less sensitive to changes in interest rates.

Example

Assume the following are 10-year, $1000 par value bonds. Current required rate of return is 10%. What is their price if rates increase by 1% to 11%.

7. Duration

Duration is the weighted-average time to maturity on an investment.

• It measures the “weighted average number of years” until an investor recovers the amount paid for the bond.

• The weight of each cash flow is calculated by dividing the present value of the cash flow by the bond’s price. Duration weighs the time at which CFs are received by the relative importance (% of total CFs) of those CFs in present value terms.

• It measures the sensitivity (or elasticity) of a fixed-income security’s price to small interest rate changes.

For zero-coupon bonds, duration = maturity.

A simple example illustrating duration.

Generalizing the above, the formula for duration is:

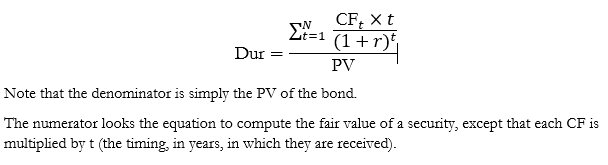
Closed formula for duration:

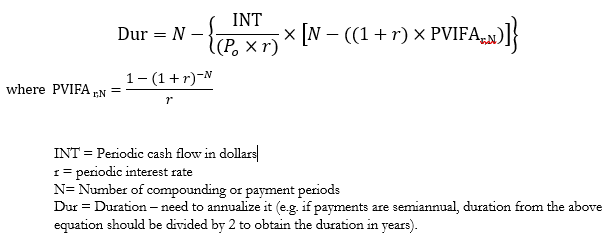
KEY CONCEPTS:

• Duration and coupon rate

  • the higher the coupon payment (rate), the shorter the bond’s duration

• Duration and yield to maturity

  • the higher the yield to maturity, the shorter the bond’s duration

• Duration and maturity

  • duration increases with maturity but at a decreasing rate.

Economic meaning of duration:

Duration measures the price sensitivity of a bond to small changes in interest rates.

The percent change in a bond’s price (%DP, or ) for a given change in interest rates (Dr) can be estimated by using duration:

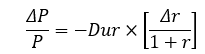
The expected $ change in price can be computed as:

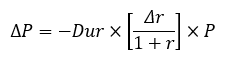
Modified duration (DurMod) can be used to predict price changes for non-annual payment loans or securities:

KEY CONCEPT:

• Duration approximation is NOT accurate for large changes in interest rates. The predicted price change for a given change in interest (using the duration) is a linear approximation of a non-linear (convex) relation between price and interest rates.

• For large increases in interest rates, duration overestimates price declines and it underestimates price increases for large decreases in interest rates.

Convexity (CX)

measures the change in slope of the price-yield curve around interest rate level r

• Convexity

incorporates the curvature of the price-yield curve into the estimated percentage price change of a bond given an interest rate change.

The duration formula can be adjusted to make it more accurate for large changes in interest rates (adjustment for convexity):