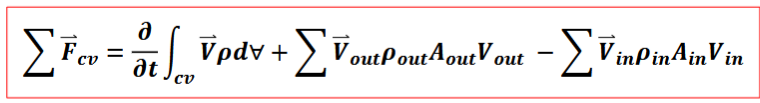biofluid mechanics exam 2

fluid dynamics & kinematics & linear momentum

Elementary Fluid Dynamics

fluid motion under assumptions of

1. Inviscid fluid - no friction force, fluid motion only governed by pressure forces and gravity

2. Steady Flow - nothing changes with time at a given location

3. Particle motion occurs along the streamline

Newton’s 2nd Law

F=ma

(Net pressure force on particle) + (Net gravity force on particle) = (particle mass) x (particle acceleration)

Velocity Vector

Ṽ, motion of each particle defined in terms of. time rate change of displacement

magnitude and direction

Streamline

lines of particle flow throughout a steady state flow field tangent to the velocity vectors

Acceleration

• time rate change of velocity

• streamwise = along streamline, a(s) = dV/dt = 𝜕V/𝜕s * ds/dt = 𝜕V/𝜕s x V

• normal = perpendicular (normal) to streamline, a(n) = V²/R

• R = radius of curvature of the streamline

Bernoulli Equation

∀ = volume. Sums forces along streamline. Used to relate hydrostatic pressure (p) to fluid height (z) and speed (V)

relationship among pressure, elevation, and velocity variation along a streamline

p + 0.5𝝆V² + 𝜸z = constant

static pressure + dynamic pressure + elevational pressure =constant (dyn+stat = stagnation pressure)

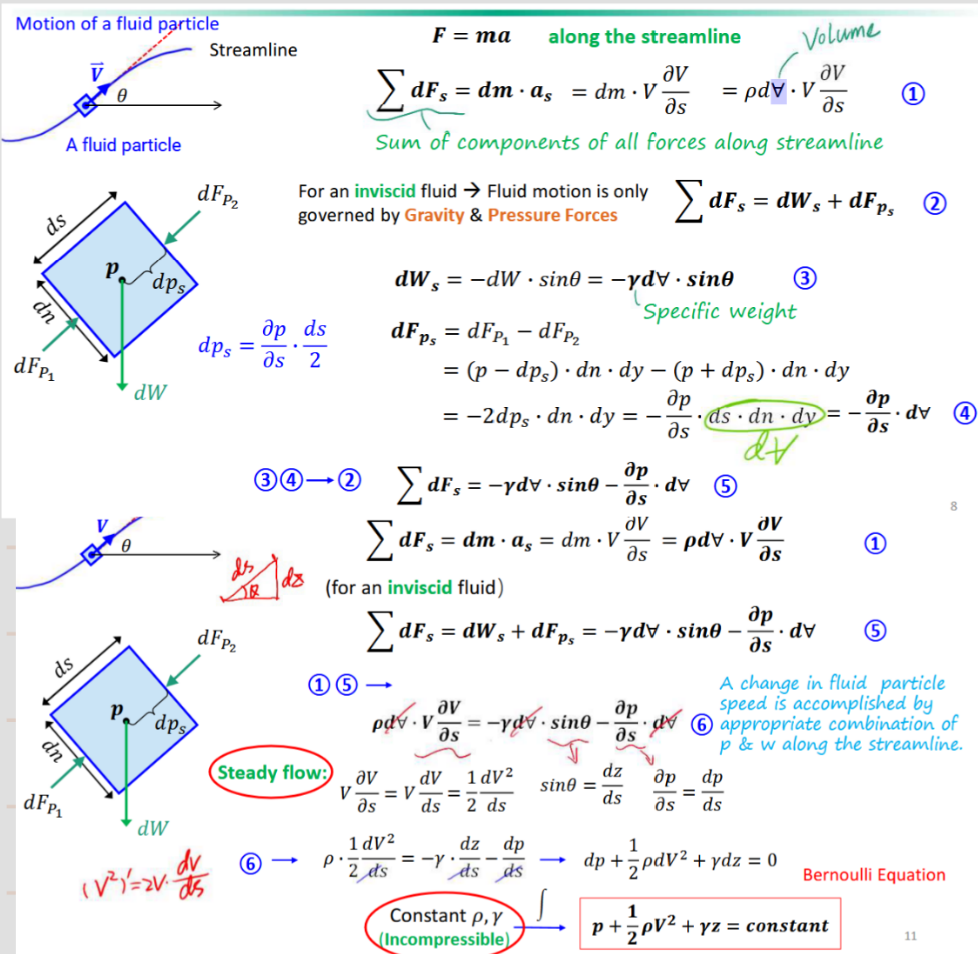
Bernouilli Equation Assumptions

1. Inviscid fluid: 𝜇 = 0

2. Steady Flow: nothing changes with time

3. Motion occurs along the streamline

4. Incompressible - constant density or 𝛾 (specific weight)

Bernouilli Equation Head Form

• P/𝜸 + V²/2g + z = H = constant. length dimension

• pressure head + velocity head (KE) + elevation head (PE) = total head

• pressure head = pressure energy = height of column of fluid to produce p = h𝜸

• velocity head = vertical distance for fluid to fall freely (no friction) to reach V from rest.

How much pressure is needed in the gills of an archerfish if it can shoot a jet of water 1 m vertically upward? Assume steady, inviscid flow.

p1 + 0.5𝝆V(1)² + 𝜸z1 = p2 + 0.5𝝆V(2)² + 𝜸z2

V1=V2=0, p2 = 0. 1 before shooting, 2 at peak of water shot

p1 = 𝜸(z2 - z1) = 9.8 × 10³ N/m³ × 1m = 9.8 × 10³ Pa

Conservation of mass

for any closed system (to mass & energy transfer) mass must remain constant over time

inflow rate = outflow rate

𝑚 = mass flow rate. Q = volume flow rate.

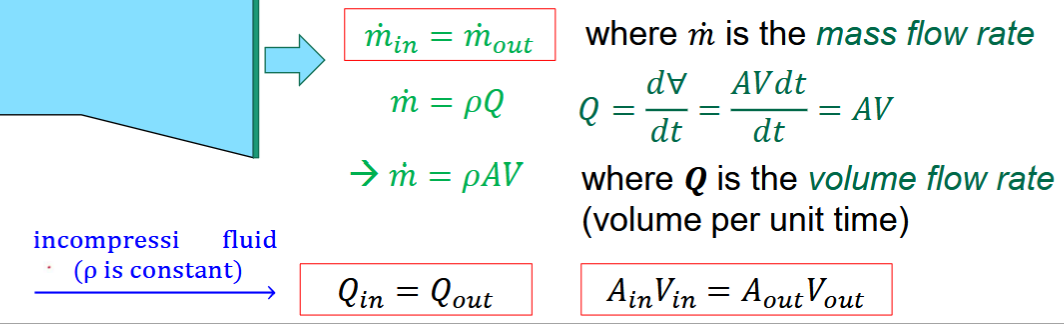
Continuity Equation

AiVi=AoVo from Qin = Qout. as area decreases velocity increases

Blood flow streamlines through from the left ventricle into the aorta can be modeled as a reducing nozzle. Model both the left ventricle and the aorta as a tube with diameter of 3.1cm and 2.7cm respectively. The pressure in the left ventricle is 130mmHg and the pressure in the aorta is 123mmHg. Blood is ejected from the left ventricle at a speed of 120cm/s. What is the blood speed at the second aorta location? Calculate the difference in height between these two
locations.

Venturi Meter

measures flowrate (Q), Bernouilli based, continuity in fluid flow in conduit with rigid walls

gage fluid, manometer. Vb > Va & zb > za → Pa > Pb flow from A to B

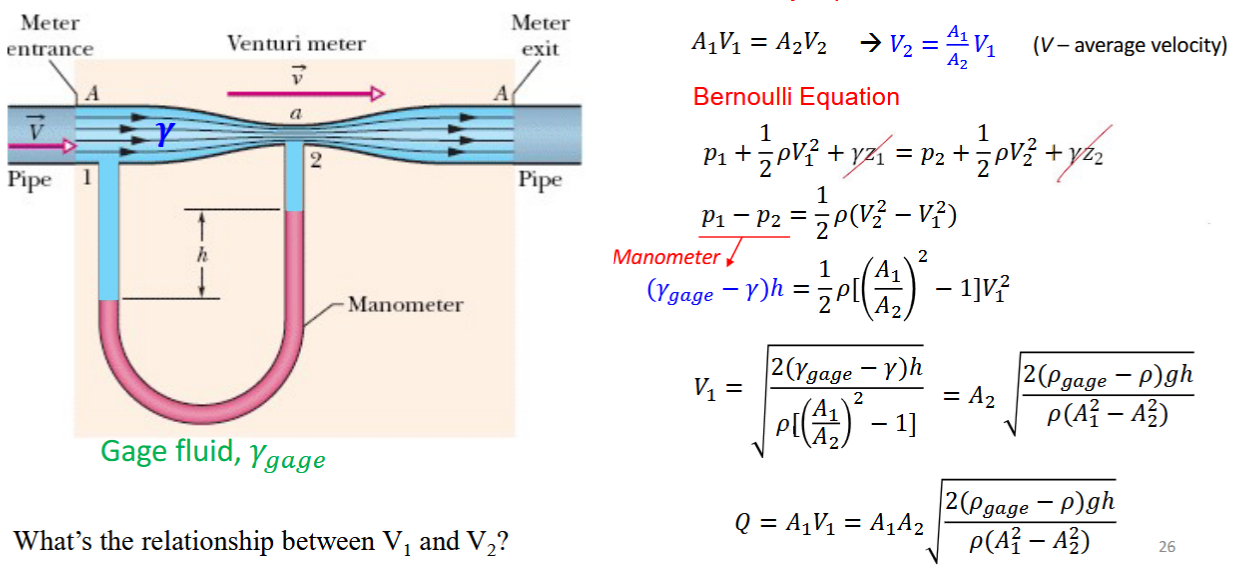
Prairie Dog Burrows

venturi tubes, air moves slower the closer it is to the surface → velocity gradient

replace used air with fresh, up to 10 meters long

one way air flow, into lower out upper based on Bernouilli equation

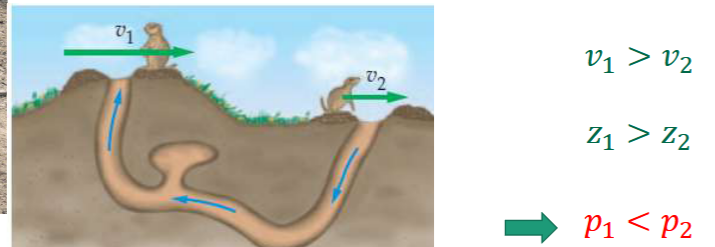
Energy Line and Hydraulic Grade Line

• measure heads, bernouilli

• energy line represents total head available to fluid

• Piezometer (p head) + pilot tube ( p + V heads) to measure heads: static p + dynamic p = stagnation p

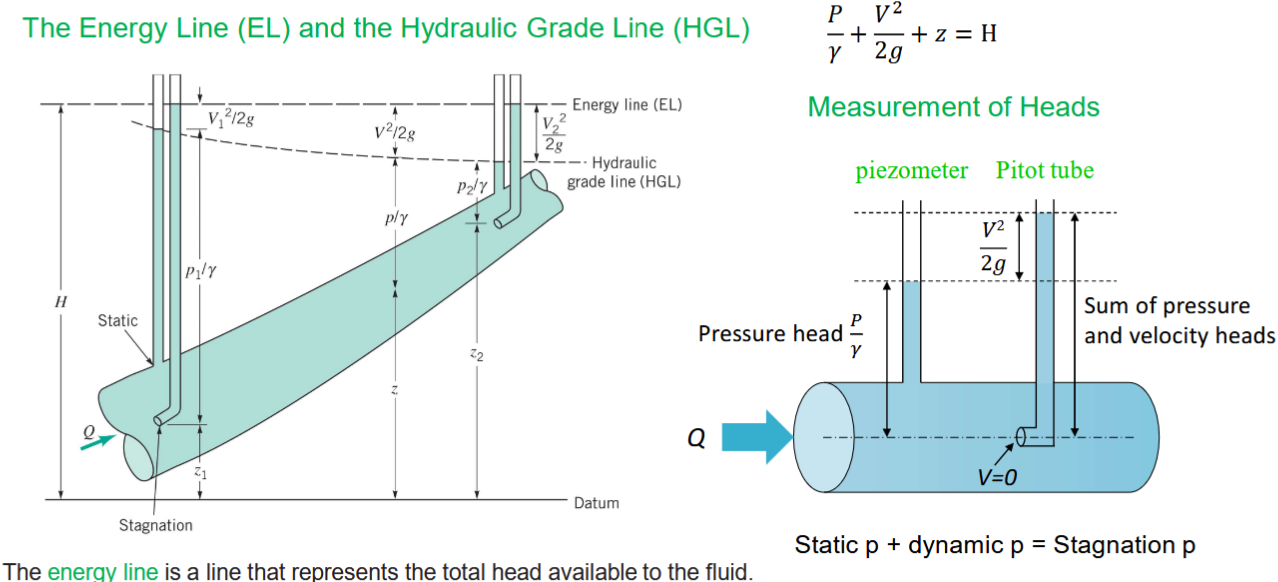
Flow Meter Equation

Fluid Kinematics

fluid motion without concern to forces necessary to create the motion

Velocity & acceleration of the fluid

Description & visualization of the fluid’s motion

Field Representation of Flow

representation of fluid parameters (density, pressure, velocity, acceleration) as function of spatial coordinates f(x,y,z) at a given instant of time

velocity and acceleration most important

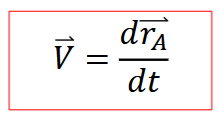
Velocity Field

velocity as function of location and time

time derivative of the position vector (r_a = relative to coordinate system, function of time if moving)

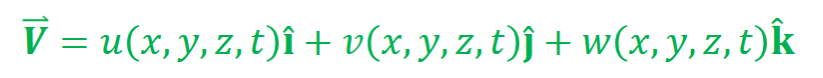
Eularian Method

stationary observer, function of position and time, easier for fluid mech

field concept - fluid motion from prescribing properties as fxns of time and space

good with many particles, fluid as a continuum

Lagrangian Method

observer moving with particles, function of time.

tracks each particle throughout flow field, point by point differential approach

good with few easily identifiable particles

Dimensional Flows

3D: V = u(x,y,z,t)i + v(x,y,z,t)j + w(x,y,z,t)k

2D: V = u(x,y,t)i + v(x,y,t)j one velocity component significantly smaller than other two

1D: V = u(x,t)i two negligible velocity requirements

Consider a velocity field given by the formula 𝑉 = (𝑢, 𝑣, 𝑤) = 2𝑥𝚤̂ − 3𝑡²𝑦𝚥̂ + 4𝑥𝑘

Is this steady flow?

No, the y component of velocity changes with time.

Streamline

line that is everywhere tangent to the velocity field. steady flow = fixed lines in space

dy/dx = v/u

aligns with streaklines & pathlines in steady flow

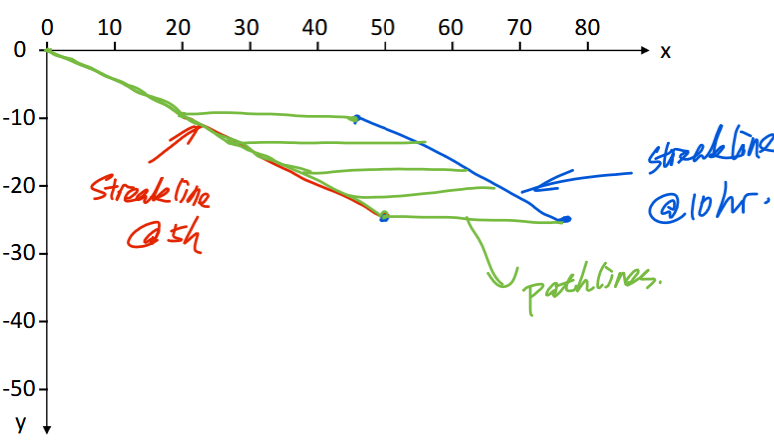
Streakline

all particles in a flow that have previously passed through P (a point)

Pathline

line traced by a particle as it flows through space as a function of time

dx/dt = u dy/dt = v

A plume of steam leaves a smokestack at x = 0 and y = 0. The plume last for 3 hrs. The wind velocity is V = 10i - 5j for the first 5 hrs, and V = 5i for the next 5hr. Show the streaklines of the plume at t = 5hrs and 10hrs.

Fluid Acceleration Lagrangian & Eularian

lagrangian: a=a(t)

eularian = acceleration field, time rate change of velocity vector

Acceleration Field 3D Vector

Types of Acceleration

1. dV/dt = local acceleration, time derivative, effects of unsteadiness of flow

2. rest = convective acceleration, spatial derivatives, contribution due to particle motion (convection) through space with a gradient in the parameter value (convective effects)

3. material acceleration = local acceleration + convective acceleration

Streamline Coordinates

s (along streamline), n (normal to streamline)

Control Volume

Fundamental physical laws: conservation of mass (continuity), newton’s laws of motion, laws of thermodynamics

volume in space through which fluid may flow. mass independent, geometric entity

given volume

System approach

collection of matter with fixed identity (same atoms or fluid particles)

flows, moves, interacts with surroundings

given mass

Reynolds Transport Theorem

Apply to use governing equations in a control volume approach
B = mb = physical parameter = mass * amount of parameter per unit mass

Finite Control Volume Analysis Governing Laws

conservation of mass - continuity equation (calc flow rates)

newton’s second law - linear momentum equation (calculate forces & torques)

first law of thermodynamics - energy equation

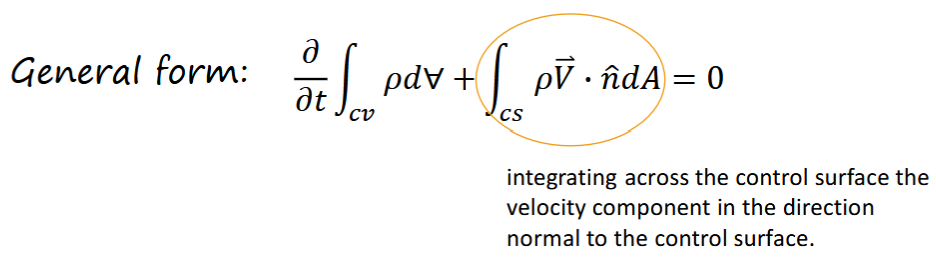
Conservation of Mass - continuity equation - cv

steady flow: m_out = m_in, 𝜕/𝜕𝑡 ∫𝜌𝑑∀ = 0, m=𝜌Q=𝜌AV if V is uniform across A

if incompressible & steady flow A1V1=A2V2

control surfaces are perpendicular to flow velocity

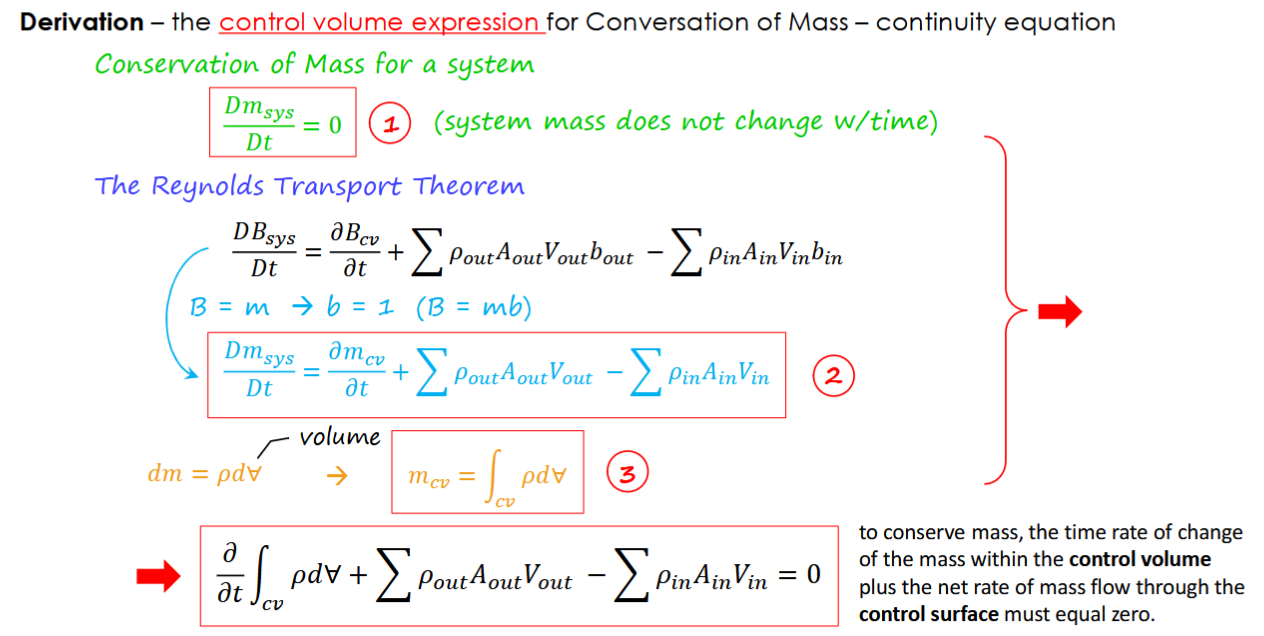
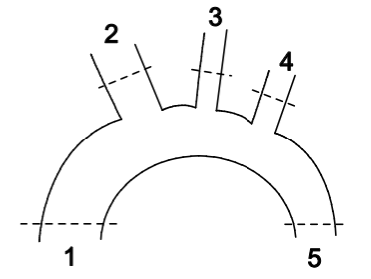
Determine the velocity of blood at cross-section 4 of the aortic arch schematized below. Assume that the diameter of the blood vessel is 3cm, 1.5cm, 0.8cm, 1.1cm and 2.7cm at cross-sections 1, 2, 3, 4 and 5 respectively. Branches 2, 3 and 4 make a 75°, 85° and a 70° with the horizontal direction, respectively. The velocity is 120cm/s, 85cm/s, 65cm/s and 105cm/s at 1, 2, 3 and 5 respectively. There is inflow at 1 and outflow at all of the remaining locations. Assume steady-flow at this particular instant in time and that the volume of interest is non-deformable.

Stream Tube

• bundle of streamlines, defined by surface formed from streamlines

• no flow crosses the surface. constant Q: Q=A1V1=A2V2

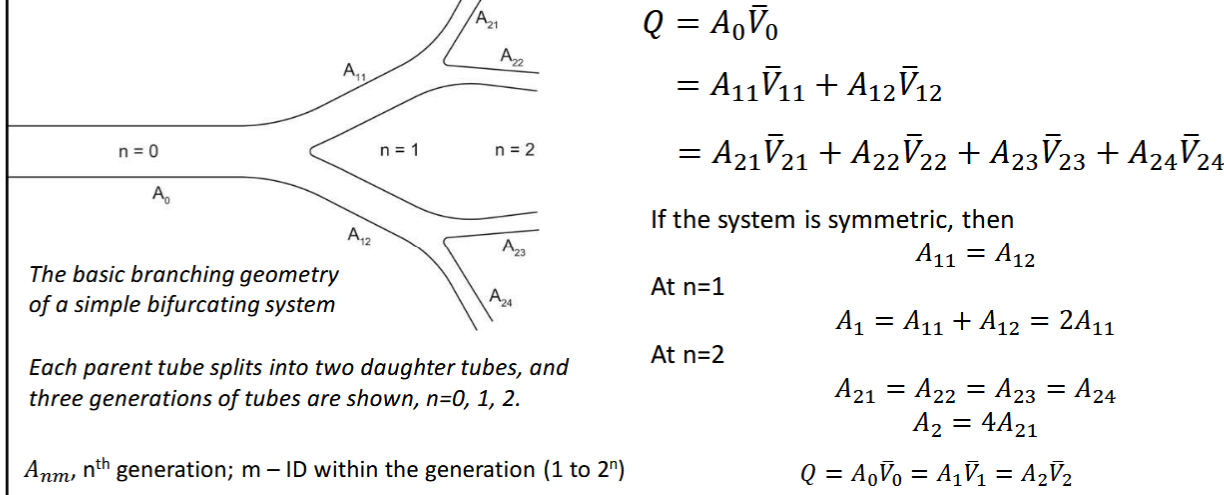
• mass conservation used to analyze gross flow features in branching networks- lung airways & vasculature

Incompressible, laminar blood flow develops in a straight blood vessel having radius R. At section (1), the velocity profile is uniform; the velocity is equal to a constant value U and is parallel to the pipe axis everywhere; At section (2), the velocity profile is axisymmetric and parabolic, with zero velocity at the pipe wall and a maximum value of umax at the centerline. 𝑢2 = 𝑢max*[1-(r/R)²].

How are U and umax related? How are the average velocity at section 2 and umax related?

Calculate the time rate of change in air density during expiration. Assume that the lung has a total volume of 6000mL, the diameter of the trachea is 18mm, the air flow velocity out of the trachea is 20cm/s and the density of air is 1.225kg/m3. Also assume that lung volume is decreasing at a rate of 100mL/s and that at the instant in time that we are measuring the system, density is uniform within the volume of interest.

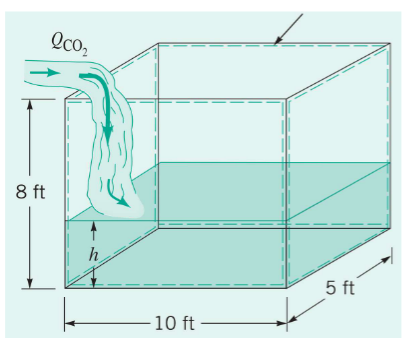
Construction workers in a trench are installing a new waterline. The trench is 10 ft long, 5 ft wide, and 8 ft deep. As a result of being near an intersection, carbon dioxide from vehicle exhaust enters the trench at a rate of 10 ft3/min. Because carbon dioxide has a greater density than air, it will settle to the bottom of the trench and displace the air the workers need to breathe. Assume that there is negligible mixing between the air and carbon dioxide.

(a) Estimate the time rate of change of the depth of carbon dioxide in the trench, in feet per minute at any instant.
(b) Calculate the time, it would take for the level of carbon dioxide to reach 6 ft, the approximate height to fully engulf the utility workers

Control Volume Velocity - moving nondeforming

1. Vcv = cv velocity = velocity of cv as seen from a fixed coordinate system

2. V = absolute velocity = fluid velocity seen by stationary observer in a fixed coordinate system

3. W = relative velocity = velocity relative to moving cv

4. V = W + Vcv. continuity equation uses W

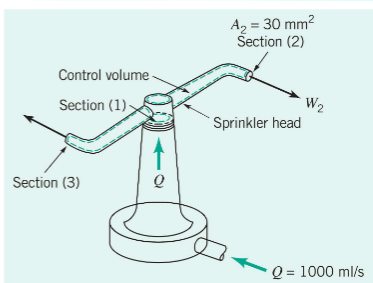
Water enters a rotating lawn sprinkler through its base at the steady rate of 1000 ml/s. The exit area of each of the two nozzles is 30 mm2.

Determine the average speed of the water leaving the nozzle, relative to the nozzle, if
(a) the rotary sprinkler head is stationary,
(b) the sprinkler head rotates at 600 rpm, and
(c) the sprinkler head accelerates from 0 to 600 rpm.

average speed of water relative to the nozzle is independent of sprinkler head speed or acceleration

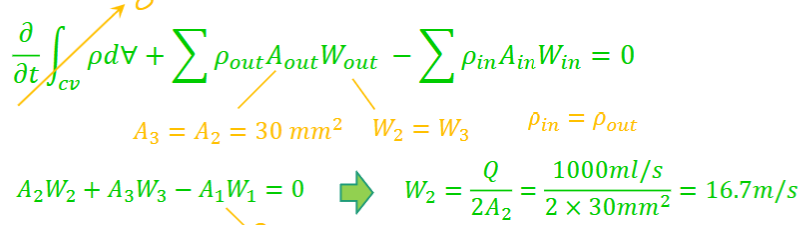
Volumetric flow rate

Q, [m³/s]

For a circular pipe with radius R, the mass flowrate 𝒎̇ = _____.

𝜌𝑽(𝝅𝑹²), uses cross sectional area

Consider steady flow through a cold pipe with constant area. If the outlet density is 80% of the inlet density 𝝆𝟐 = 𝟎. 𝟖 𝝆𝟏 then the outlet velocity V2 = _____ V1.

1.25

A stationary observer sees water leaving a rocket at 3 m/s downwards. The water makes the rocket travel upwards at 1 m/s. The water's relative velocity with respect to the rocket is _____ m/s.

-4

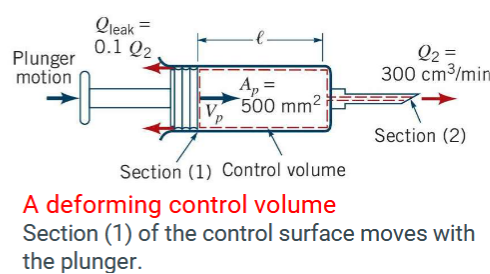
A syringe is used to inoculate a cow. The plunger has a face area of 500 mm2. The liquid in the syringe is to be injected steadily at a rate of 300 cm3/min. The leakage rate past the plunger is 0.10 times the volume flowrate out of the needle.

With what speed should the plunger be advanced?

Basic Laws → cv Equations

Reynolds Transport Theorem

conservation of mass → continuity

newton’s 2nd law of motion → linear momentum equation

1st law of thermodynamics → the energy equation

Linear Momentum Conservation

momentum of sys cannot be changed wo action of a force

time rate change of momentum = F

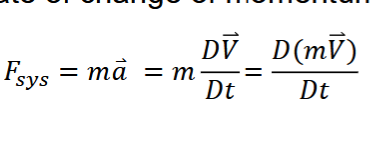
Linear Momentum Derivation

1st term = time rate change of linear momentum of contents of cv

2nd term = net flow of linear momentum through control surface = momentum flux

vector equation of external forces

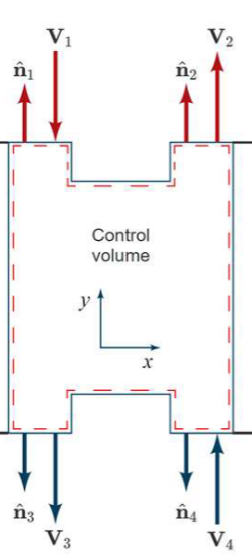
A control volume is shown with 4 sections. Sections 1 and 4 are inlets while sections 2 and 3 are outlets. Each section has a normal vector 𝒏 and a velocity vector 𝑽. Of special interest is the sign of the momentum flux term. Which section has positive momentum flux? Select all that apply.

sections 2 & 3

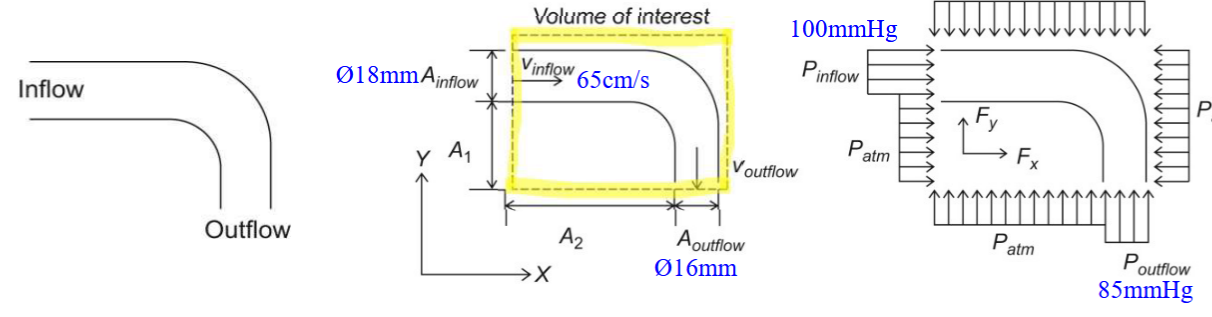
Determine the force (FA, Anchoring force) required to hold the brachial artery in place during peak
systole. Assume at the inlet the pressure is 100mmHg and at the outlet the pressure is 85mmHg
(these are gage pressures). The diameter of the brachial artery is 18mm at the inflow and 16mm at
the outflow. The blood flow velocity at the inlet is 65cm/s. For simplicity neglect the weight of the
blood vessel and the weight of the blood within the vessel.

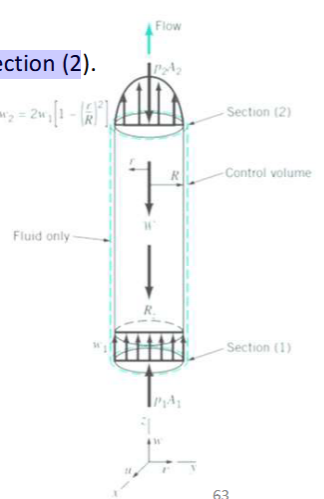
Incompressible, laminar water flow develops in a vertical straight pipe having radius R shown as below. At section (1), the velocity profile is uniform; the velocity is equal to a constant value U and is parallel to the pipe axis everywhere. At section (2), the velocity profile is axisymmetric and parabolic, with zero velocity at the pipe wall and a maximum value of umax at the centerline.

Develop an expression for the fluid pressure drop that occurs between section (1) and section (2).

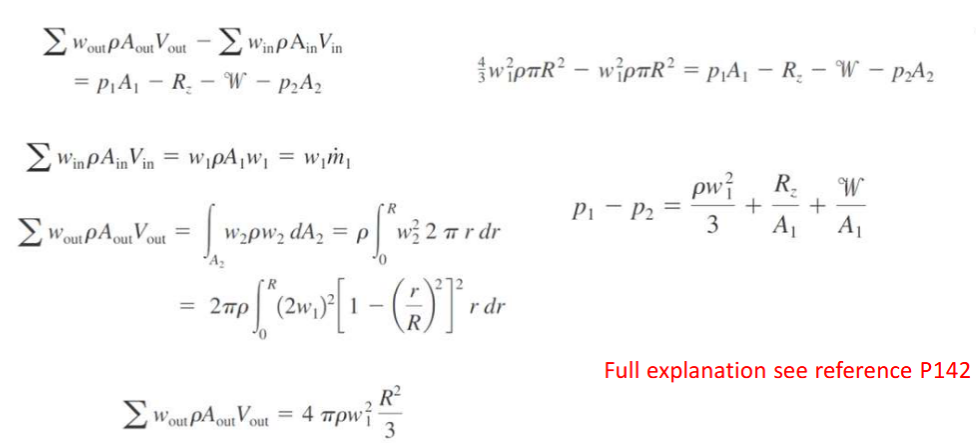
Linear Momentum General Equation

directional (pos or neg), time rate change = 0 for steady state but the time rate change of the system is not 0.

may need to use gage pressure, only considers external forces

Fx from u, Fy from v, Fz from w