Geometry: Diliations and similarity

What does "prime" mean and what is it represented by?

"Prime" refers to the new image or point after a transformation, such as a dilation. It is often represented with a symbol (like A') or a number (A1, A2, etc.) to show the position of the transformed point relative to the original.

What is dilation?

Dilation is a transformation that changes the size of a figure but keeps its shape. It involves expanding or contracting the figure based on a center of dilation and a scale factor.

What does "the center of dilation" mean?

The center of dilation is the fixed point from which the figure is dilated. All points in the figure are moved along lines that radiate out from this center, either getting closer (shrinking) or farther away (expanding), depending on the scale factor.

When writing down coordinates always make sure to use…

parenthesis and commas, like this: (A,B)

What is a scale factor?

A scale factor is the ratio that describes how much the figure is enlarged or reduced during dilation.

• If the scale factor is greater than 1, the figure enlarges.

• If the scale factor is between 0 and 1, the figure shrinks.

• A scale factor of 1 means the figure stays the same size.

When dilating something, do you multiply or divide?

You multiply the distances by the scale factor. This changes the size of the figure but keeps the proportional relationships between the points the same.

How do you dilate something?

1. Identify the center of dilation.

2. Calculate the distance between each point on the figure and the center of dilation.

3. Multiply the distance by the scale factor.

4. Plot the new points at the scaled distances from the center.

What does it mean to multiply by a fraction?

Multiplying by a fraction means you are reducing the size of the figure. The fraction represents the new ratio of the dilated size to the original size. For example, a scale factor of 12\frac{1}{2}21​ means the figure will shrink to half its original size.

What does it mean to multiply by a fraction?

Multiplying by a fraction means you are reducing the size of the figure. The fraction represents the new ratio of the dilated size to the original size. For example, a scale factor of ½ ​ means the figure will shrink to half its original size.

What is the process of dilating line segments?

• Identify the center of dilation (it could be any point, not necessarily the origin).

• For each endpoint of the line segment, measure the horizontal and vertical distances from the center of dilation.

• Multiply both the horizontal and vertical distances by the scale factor.

• The new endpoints will be located at the scaled distances along the same lines from the center.

  Why do we multiply both distances?
  To keep the shape of the figure intact. Dilating each coordinate in both directions ensures the proportions of the line segments remain consistent.

What does it mean to preserve the direction, and why is it important?

Preserving the direction means that when a figure is dilated, the orientation of the points remains the same. For example, if a point is to the right of the center of dilation, it will still be to the right after dilation. This is important because dilation doesn't just resize figures, it also maintains their relative positions and orientations, ensuring that the shape of the figure stays consistent.

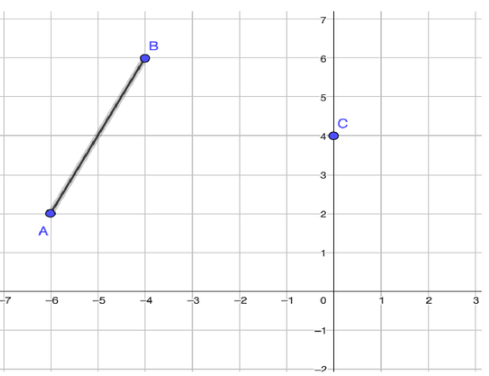
State the coordinates of A' and B' after a dilation of 1/2 centered at point C.

A' = (−3,3)
B'= (−2,5)

When dilating always start from ________.

your center of dilation

A' = ____
B'= ____

A' = (6,−5)
B' = (10,3)

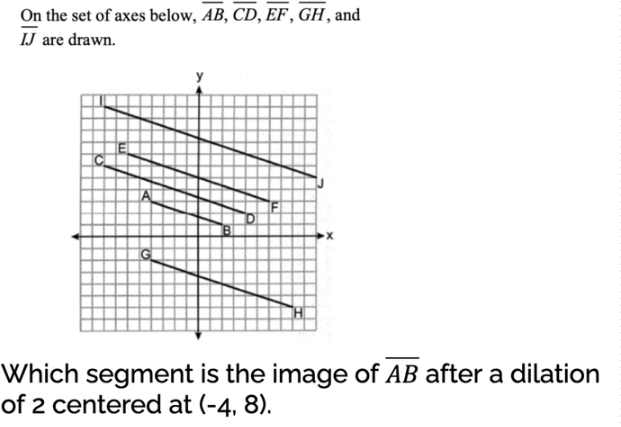
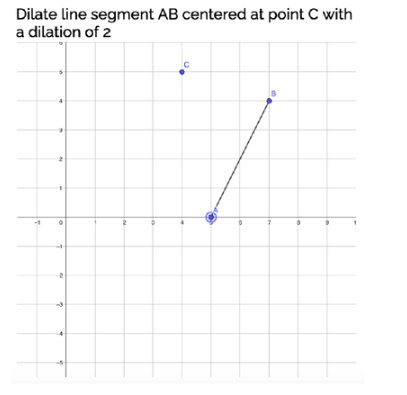
Which segment is the image AB after a dilation of 2 centered at (-4,8)

GH

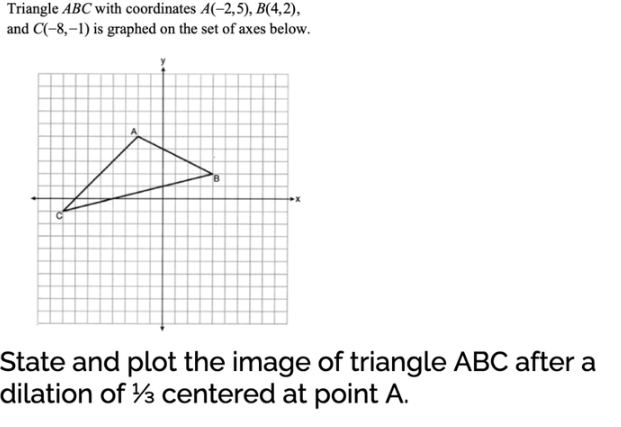
State and Plot the points on paper (Or on a website) and write the points below. Be sure to put parenthesis.

A' = ____
B'= ____

C’ = _____

A'= (−2,5)
B' = (0,4)
C'= (−4,3)

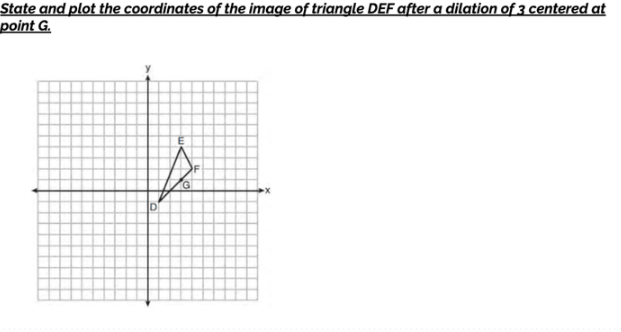
Remember to plot your points on paper (or a website)

D'=
E'=
F'=

D'=(−3,−5)
E'=(3,10)
F'=(6,4)

Plot your coordinates on paper (or a website) and state your coordinates below

J'=
O'=
E'=

J'=(4,6)
O'=(−8,2)
E'=(8,−6)

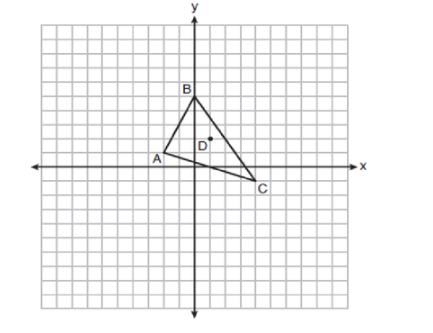
Triangle ABC and point are graphed on the set of axes below.
Graph and label (on paper) triangle A'B'C', the image of triangle ABC , after a dilation of scale factor 2 centered at point D.
Then state the points for A', B' And C' below.

A' =
B' =
C' =

A' = (−5,0)
B' =(−1,8)
C' = (7,−4)

What is the center of dilation in geometry?

The center of dilation is the fixed point in a plane about which all points of a figure are expanded or contracted. It acts as the “anchor” that stays in place while the figure changes size. Every point in the original shape, when connected to its image after dilation, passes through the center of dilation.

How can you find the center of dilation using a graph with two similar figures?

Draw straight lines connecting each point in the original figure to its corresponding point in the dilated figure. The point where at least two of those lines intersect is the center of dilation. Using a ruler helps ensure precision since small errors can change where the lines meet.

hat is the formula for the scale factor in a dilation?

The formula for the scale factor is

Scale factor = New length/Old length

This ratio tells you how much larger or smaller the new figure is compared to the original.

If the original side length is 6 and the new side length is 3, what is the scale factor?

The scale factor is 3/6 = 1/2. That means the image is half the size of the original, so it is a reduction. Every distance from the center of dilation to point on the shape is now half as long.

The scale factor formula is ________ divided by ________.

New divided by old. This means you take the measurement from the dilated figure and divide it by the measurement from the original figure. It shows the ratio of enlargement or reduction.

What does a scale factor less than 1 mean?

A scale factor less than 1 means the image is smaller than the original — this is called a reduction. The points of the image are closer to the center of dilation than those of the original shape. For example, a scale factor of ½ ​ shrinks all distances by half.

What does a scale factor greater than 1 mean?

A scale factor greater than 1 means the image is larger than the original — this is called an enlargement. The points move farther away from the center of dilation. For example, a scale factor of 4 makes every length four times longer than the original.

How can the scale factor confirm the correct center of dilation?

Once you guess the center by drawing lines, you can test it using the scale factor. Measure how far each point moved from that center and see if the distances match the ratio found. If they do, your center of dilation is correct; if not, your intersection point may be slightly off.

If the scale factor is 1/3​, what does that tell you about the dilation?
A) The image is three times larger
B) The image is one-third the size of the original
C) The image and original are congruent
D) The image has no center of dilation

B) The image is one-third the size of the original. This means it’s a reduction, and all distances from the center of dilation are one-third as long as before.

What are two common sources of error when finding the center of dilation on paper or a screen?

Common errors include drawing lines that are slightly off-angle and using inconsistent points between the original and image. Even a tiny error in line placement can cause the intersection to shift. Using a ruler, aligning carefully, and confirming with the scale factor helps reduce these mistakes.

Why might someone choose different points (like L and L’ then also A and A’) when finding the center of dilation?

Any corresponding sides can be used because the dilation affects all points in the same way. Using different pairs of points helps double-check accuracy, especially if one pair is hard to measure. It also provides variety, so you don’t rely on only one side that could have a drawing error.

If the scale factor is 1/2, moving from the smaller shape to the larger one means you must ________ the distances.

Double. Since the larger shape is twice the size of the smaller one, each coordinate change from the center of dilation must be multiplied by 2. This confirms that the scale factor works both ways — enlargement and reduction.-

What is one reason to calculate the scale factor after guessing the center of dilation?

Calculating the scale factor afterward allows you to test whether your drawn intersection is correct. If the distances from the supposed center match the ratio of the scale factor, the center is accurate. It’s a way to mathematically verify a geometric estimate.

Which of the following is not true about dilation?
A) It changes the size of a figure
B) It changes the shape of a figure
C) It has a fixed center point
D) It uses a scale factor

B) Dilation does not change the shape of a figure — only its size. The figure remains similar to the original.

What should you always use when drawing lines to find a center of dilation?

A ruler or straightedge is essential to maintain precision. Even a small wobble can cause the lines to miss the true intersection. Careful, neat drawing ensures that the visual method matches the numerical scale factor check.

When the scale factor is 2, every distance from the center of dilation is ________ as long.

Twice. Each point in the image is double the distance from the center compared to the original. That’s what creates an enlargement.

How do you confirm a scale factor of 1/3​ visually?

From the center of dilation, measure the movement of a point to its image. The new movement should be one-third of the original distance if it’s a reduction. Conversely, going the other way (from small to big) should triple the distance.

What happens to coordinates during dilation when the center is the origin (0,0)?

Each coordinate is multiplied by the scale factor. For example, if the scale factor is 2 and the original point is (3,4), the image point becomes (6,8). This makes it easy to compute dilations algebraically when the center is at the origin.

Why is the scale factor method useful when doing dilations digitally (like in online flashcards)?

Because you can’t draw or measure directly on the screen, using ratios and coordinates allows you to confirm answers numerically. It replaces the need for drawing tools while still verifying geometric relationships. Understanding the math behind the visuals is key in these situations.

What is the simple algebraic equation that describes a dilation?

X′=C+k(X−C). It shows that the new point X′ lies along the line from the center C through the original point  X, stretched or shrunk by a scale factor k. This is the most compact and general form of a dilation equation.

𝑋′=𝐶+𝑘(𝑋−𝐶)X′ the letter C stands for ________.

The center of dilation. It’s the fixed point around which the figure expands or contracts. Every line from C to X extends through X' in a straight path.

How can you rearrange X' = C + k(X - C) to solve for the center C?

Subtract C from both sides and expand to get X' - C = k(X - C). Then you can solve for C algebraically or split into x and y coordinates. This leads to the formulas a = (x2 - kx1) / (1 - k) and b = (y2 - ky1) / (1 - k).

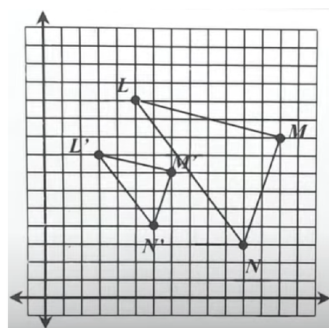
Find the center of dilation and the scale factor. Write the scale factor as a fraction in simplest form.

The center of dilation is (1,5)
The scale factor is ½ ​

Use drawing method or this formula:

SKIPPYSKIPSKIPS

SKIP

When k (Scale factor) > 1, the image point X' is ________ from the center than the original point.

Farther. The figure enlarges because the distances from the center are multiplied by a number greater than 1. This is how dilation creates a bigger but similar image.

What happens if the scale factor k = 1 in X' = C + k(X - C)?

If k = 1, then X' = X, meaning there is no change in size or position. The figure stays exactly the same because each point remains the same distance from the center. This is essentially a “no dilation” transformation.

What information do you need to find the center of dilation algebraically?

You need at least one pair of corresponding points — one from the original figure and one from the dilated image — and the scale factor. With those values, you can plug into the formulas for a and b. More pairs help verify your result is consistent.

How do you find the x-coordinate of the center of dilation using points and a scale factor?

Use the formula a = (x’ - kx) / (1 - k). Here x is the original x-value, x’ is the dilated x-value, and k is the scale factor. This tells you exactly where the center lies horizontally.

How do you find the y-coordinate of the center of dilation using points and a scale factor?

Use the formula b = (y’ - ky1) / (1 - k). This works just like the x-coordinate formula but finds the vertical position of the center. Together, the two coordinates give the full center (a, b).

The formula for finding the center of dilation is a = (x' − kx1) / (1 − k) and b = (y’ − ky1) / (1 − k), where (a, b) = ________.

The coordinates of the center of dilation. These formulas come from rearranging the dilation equation for x and y. They allow you to solve for the center without needing to draw lines.

You know X(4, 2) → X'(10, 8) and the scale factor is 2. What is the center of dilation?

A) (2, 1)
B) (−2, −4)
C) (−4, −4)
D) (0, 0)

B) (−2, −4). Using a = (10 − 2×4)/(1 − 2) = −2 and b = (8 − 2×2)/(1 − 2) = −4, we find the center. Checking with both coordinates confirms the same point.

Why is this algebraic method useful for online or non-graphing work?

Because you can’t draw or measure, the formula gives a precise way to calculate the center numerically. It removes the guesswork and works even when you only have coordinates and a scale factor. It’s especially helpful for digital quizzes or geometry software.

To check if a guessed center is correct, the distances from the center to the original and image points should have a ratio equal to ________.

The scale factor. If the distances follow the same ratio, the guessed center is correct. This rule holds true whether you find it visually or algebraically.

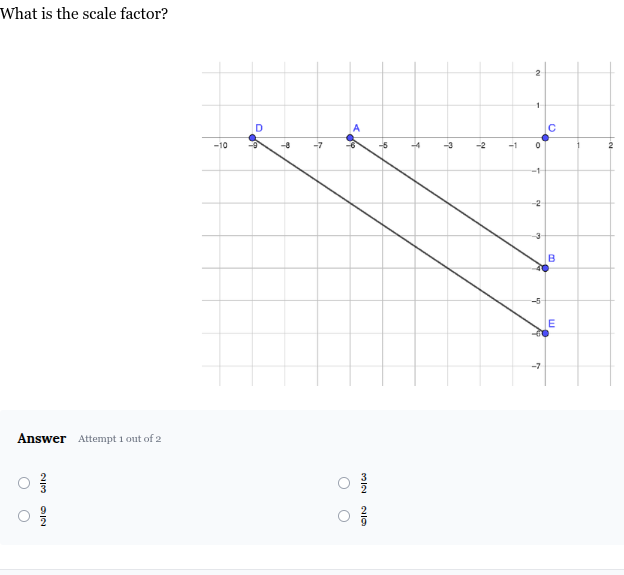
In the diagram below, DE is the image of AB after a dilation centered at the origin. The coordinates of the vertices are A(-6, 0), B(0, -4), D(-9,0) and E(0, -6).

What is the scale factor?

3/2. K = x’/x

Look at the question below.

Choice 3

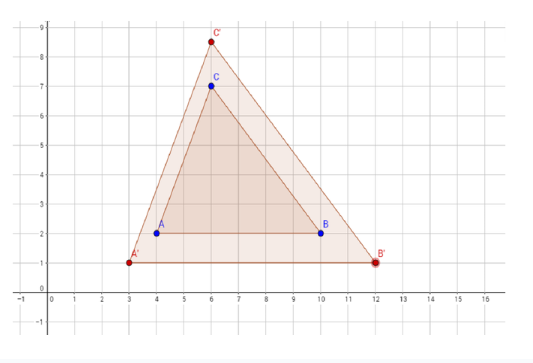
Find the scale factor and center of dilation. WRITE THE SCALE FACTOR IN SIMPLEST FRACTION FORM.

The center of dilation is (6,4)
The scale factor is 3/2

What is a scale factor in geometry?

The scale factor is the number you multiply the dimensions of a figure by to enlarge or reduce it during a dilation.

How do you find the scale factor using sides of similar figures?

Divide a side of the image by the corresponding side of the original figure.
Example:
Original side = 4 cm, Image side = 12 cm

Scale factor  = 12/4 = 3

True or False: The scale factor is always positive.

True — it represents a size change, not direction.

A triangle has a side of 5 cm. After dilation, the side is 15 cm. What is the scale factor?

15/5 = 3cm

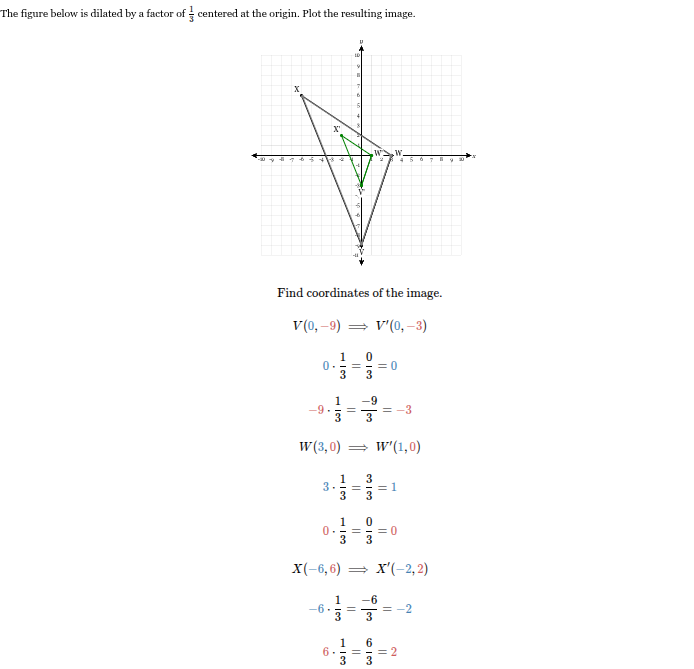
The figure below is dilated by a factor of 1/3 ​ centered at the origin. Plot the resulting image using graph paper (online or offline).

Should look like this

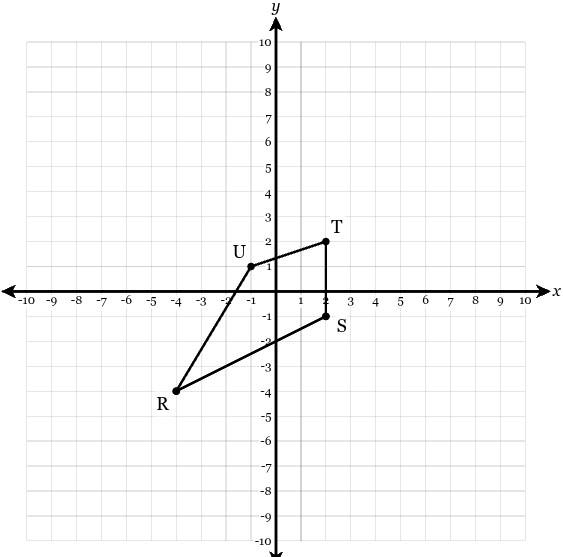
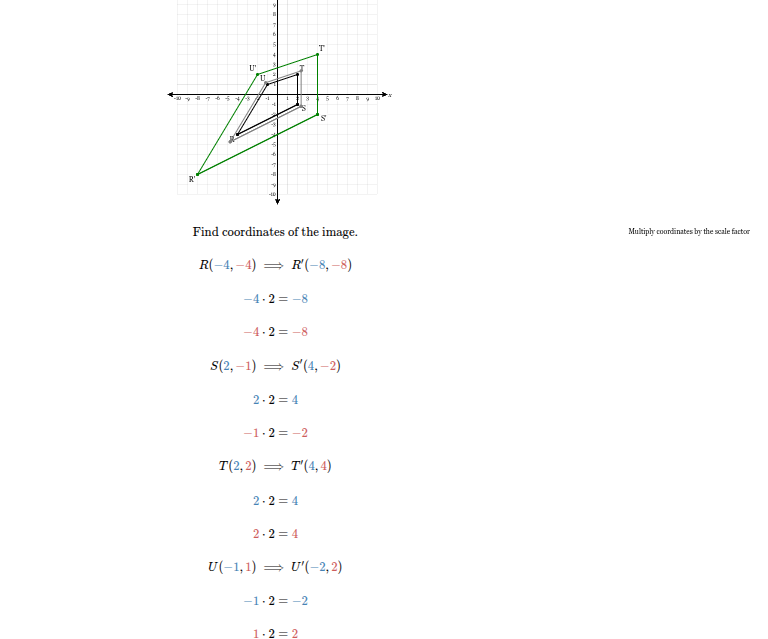
The figure below is dilated by a factor of 2 centered at the origin. Plot the resulting image using graphs paper.

Should look like this

The figure below is dilated by a factor of 3/2 centered at the origin. Plot the resulting image.

Should look like this

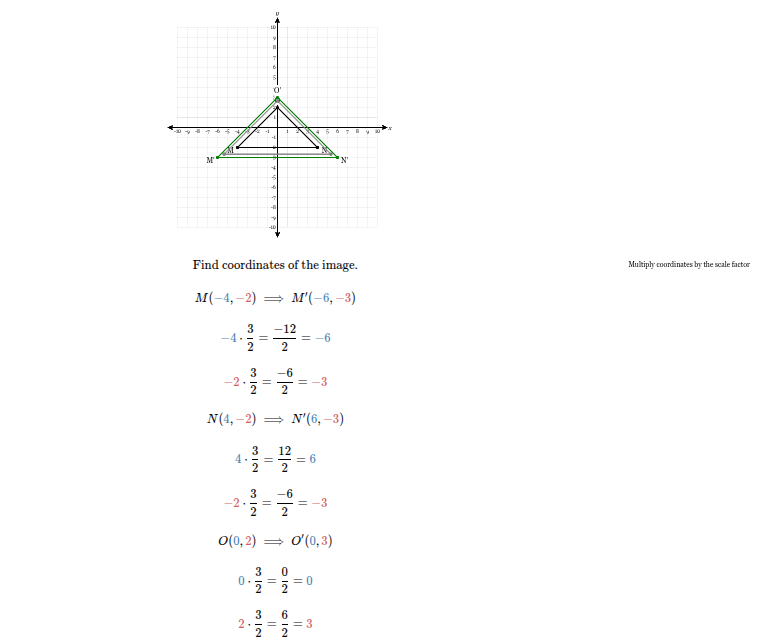
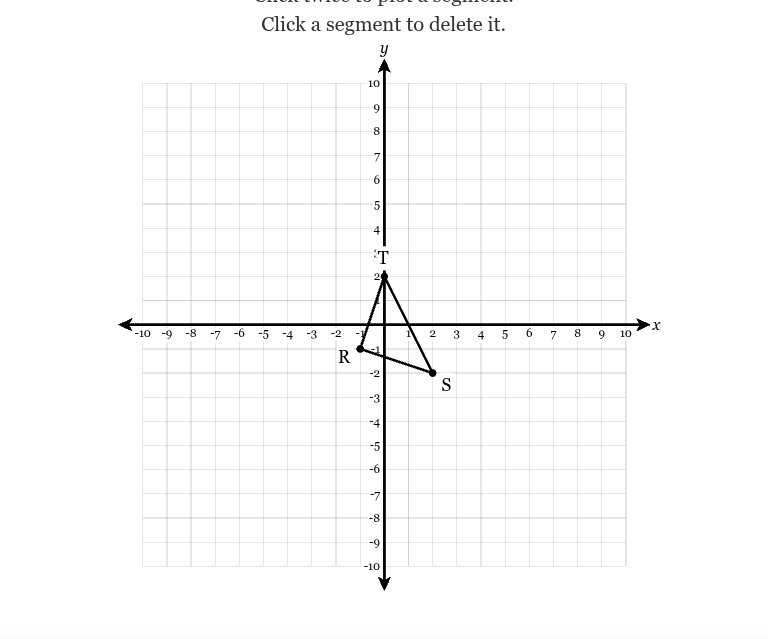
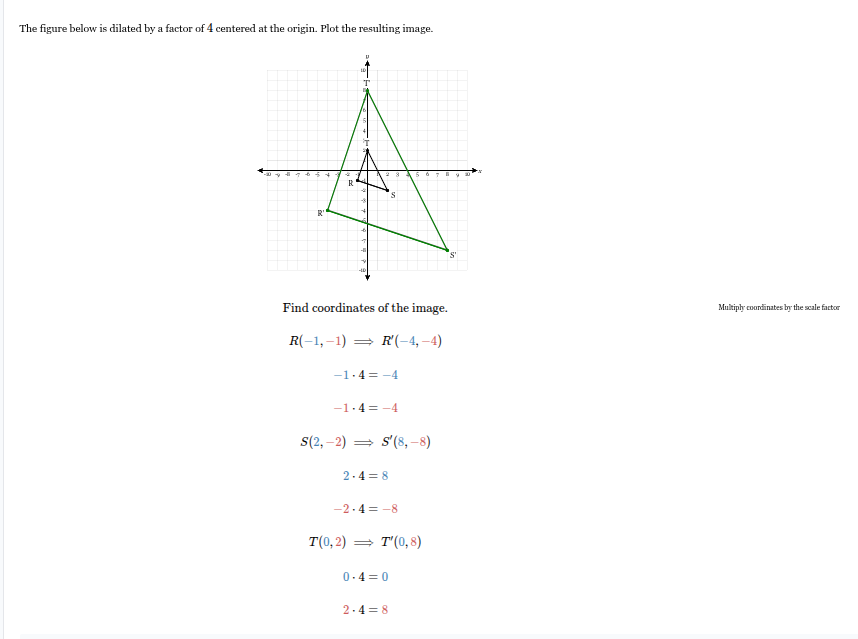
The figure below is dilated by a factor of 4 centered at the origin. Plot the resulting image.

Should look like this

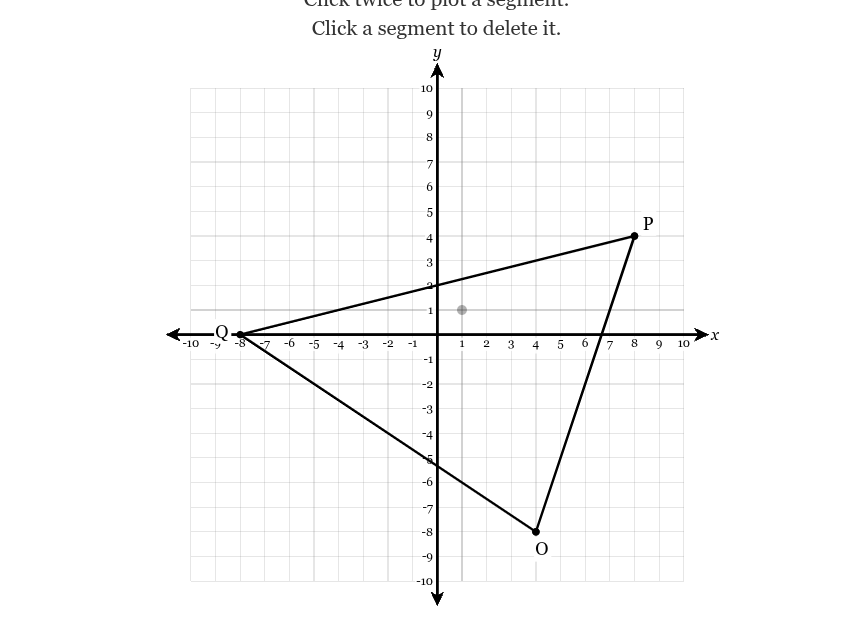
The figure below is dilated by a factor of 1/4 centered at the origin. Plot the resulting image.

Should look like this 

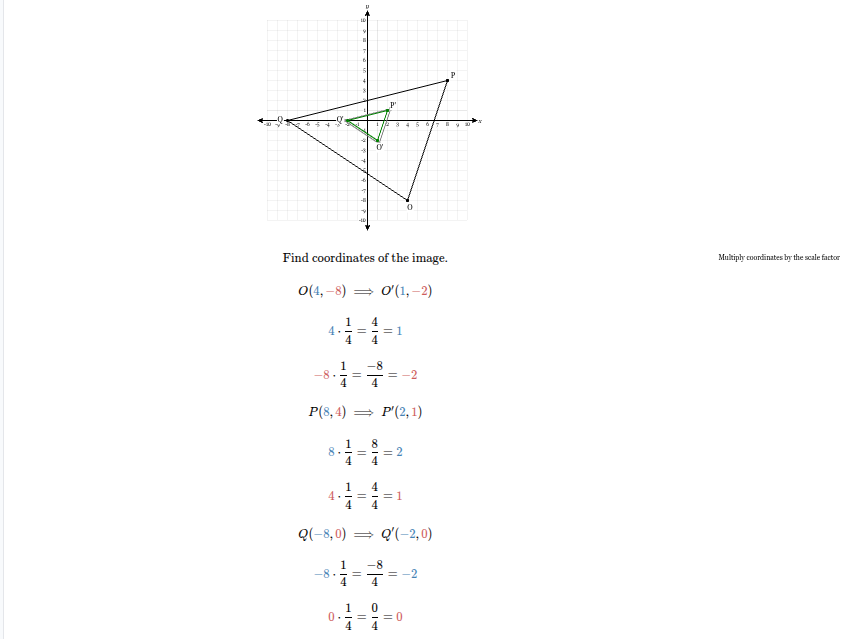
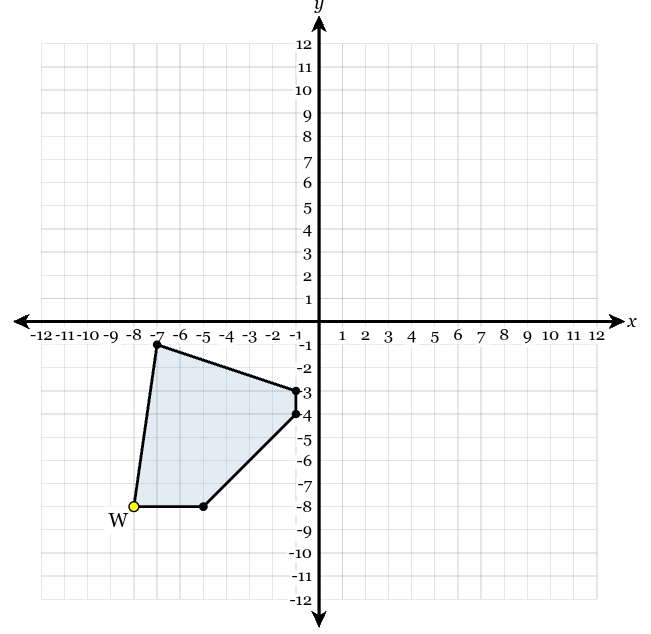
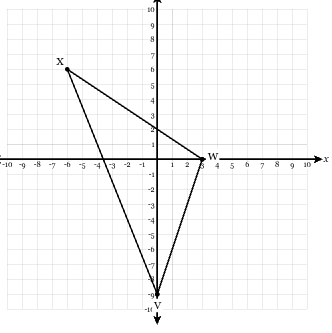
The figure below is dilated with the center of dilation at the origin and a scale factor of 1/4​ and then rotated 180° counterclockwise. What are the coordinates of the image of point W after these transformations?

(2,2)

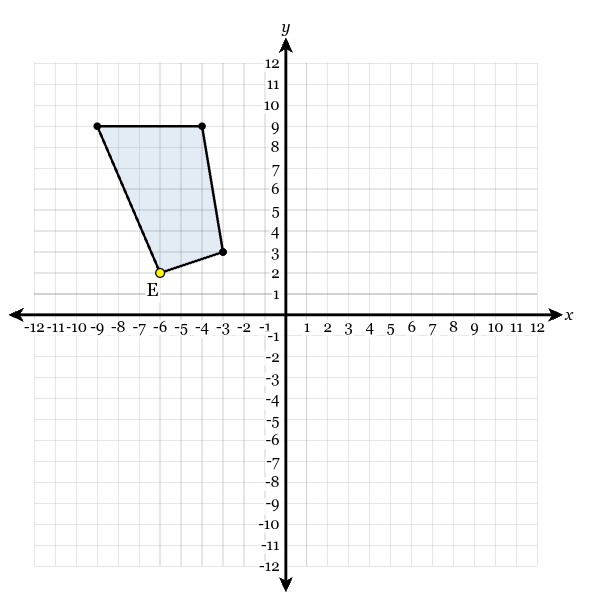
The figure below is rotated 180° clockwise and then dilated with the center of dilation at the origin and a scale factor of 1/2​. What are the coordinates of the image of point E after these transformations?

(3,−1)

The figure below is reflected over x-axis and then dilated with the center of dilation at the origin and a scale factor of 1/3​. What are the coordinates of the image of point P after these transformations?

(−3,2)

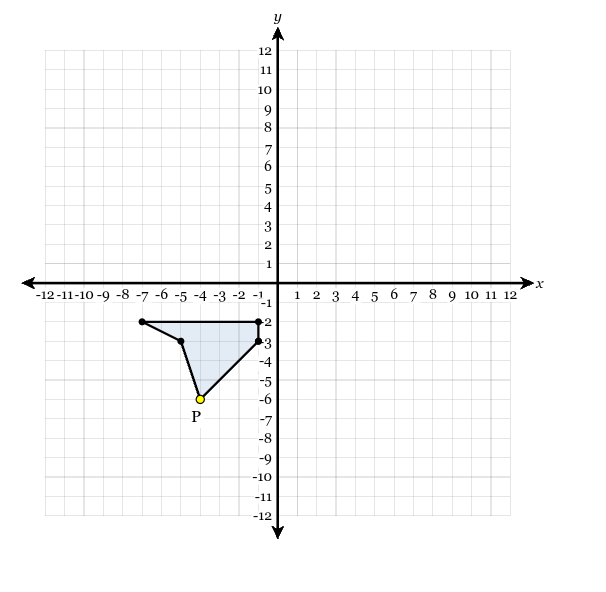
The figure below is dilated with the center of dilation at the origin and a scale factor of 1/2​ and then reflected over x-axis. What are the coordinates of the image of point P after these transformations?

(−2,3)

What is slope?

Rise/run or (y₂ - y₁)/(x₂- x₁)

Whenever two lines have the same slope they are _____

parallel

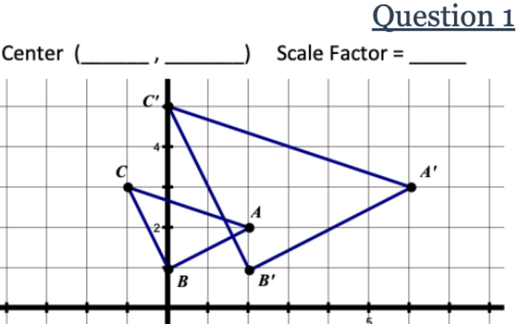
The Center of dilation is___

The scale factor is__

(-2,1)

2

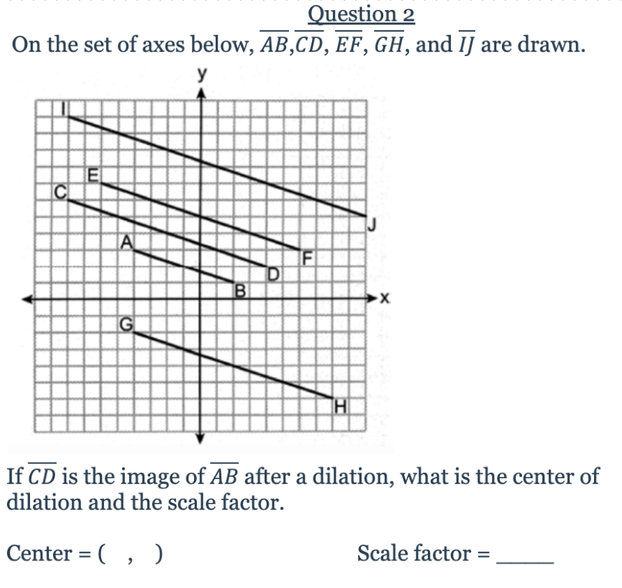
Briefly explain how you arrived at your answer.

The Center of dilation is ____
The scale factor is ___

The Center of dilation is (0,0)
The scale factor is 2

Scale factor = ___

Center of dilation = ____

Briefly explain how you got at your answer

The Center of dilation is (3,5)
The scale factor is 2

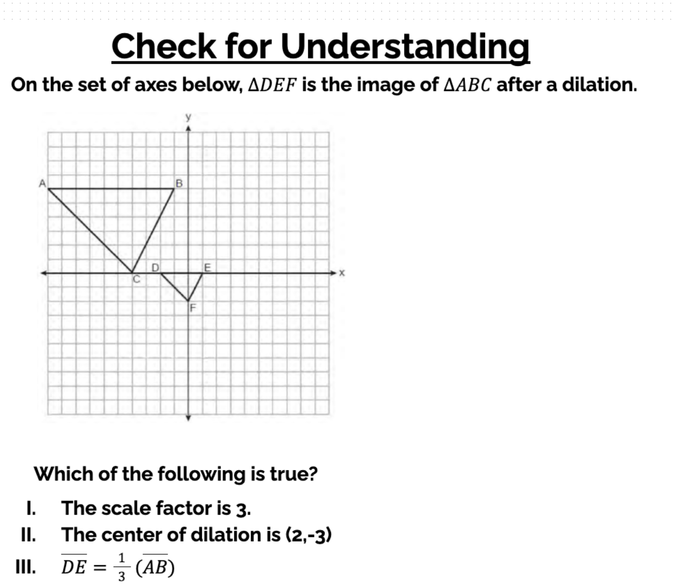
1) I only

2) II only

3) II and III only

4) I, II and III

3) II and III only

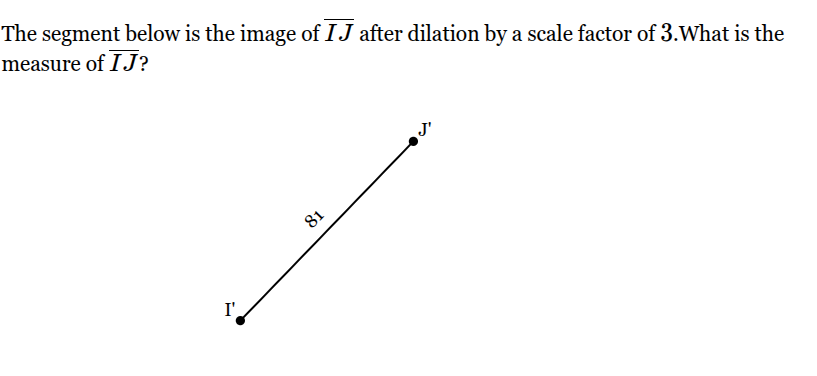
How long is IJ?

27

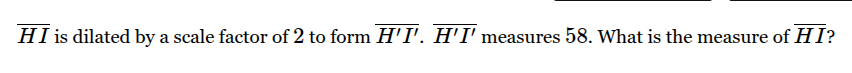
29

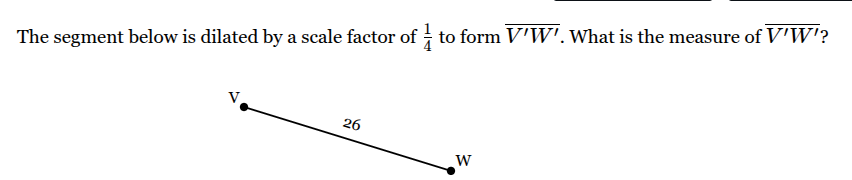
6.5 or 13/2

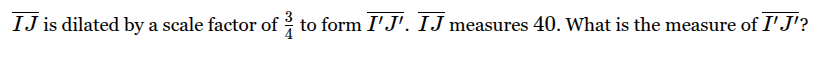
30

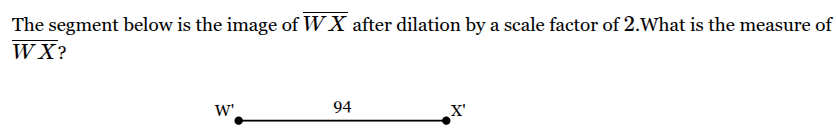
47

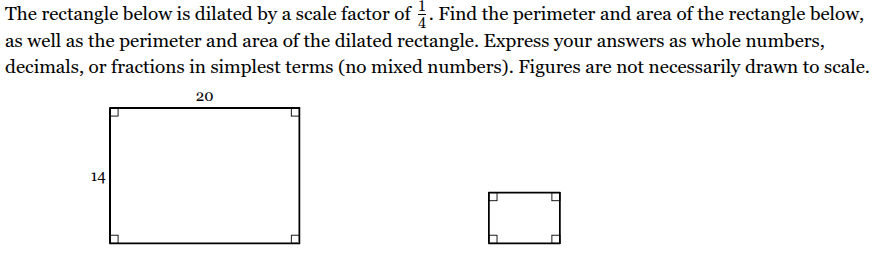
The rectangle below is dilated by a scale factor of one 1/4 ​. Find the perimeter and area of the rectangle below, as well as the perimeter and area of the dilated rectangle. Express your answers as whole numbers, decimals, or fractions in simplest terms (no mixed numbers). Figures are not necessarily drawn to scale.

Perimeter of given rectangle: ____ units

Perimeter of dilated rectangle: ____ units

Area of given rectangle: ____ units²

Area of dilated rectangle: ____ units²

Perimeter of given rectangle = 68 units.
Area of given rectangle = 280 units².
Perimeter of dilated rectangle = 17 units.
Area of dilated rectangle = 35​/2 units².

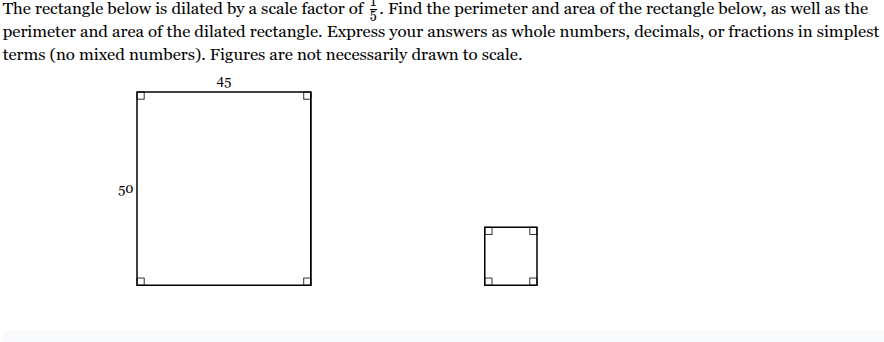
The rectangle below is dilated by a scale factor of 1/5​. Find the perimeter and area of the rectangle below, as well as the perimeter and area of the dilated rectangle. Express your answers as whole numbers, decimals, or fractions in simplest terms (no mixed numbers). Figures are not necessarily drawn to scale.

Perimeter of given rectangle _____ units

Perimeter of dilated rectangle ______ units

Area of given rectangle_____  units²

Area of dilated rectangle _____ units²

Perimeter of given rectangle = 190 units.
Area of given rectangle = 2250 units².
Perimeter of dilated rectangle = 38[ units.
Area of dilated rectangle = 90 units².

The rectangle below is dilated by a scale factor of 5. Find the perimeter and area of the rectangle below, as well as the perimeter and area of the dilated rectangle. Express your answers as whole numbers, decimals, or fractions in simplest terms (no mixed numbers). Figures are not necessarily drawn to scale.

Perimeter of given rectangle ____ units

Perimeter of dilated rectangle ______ units

Area of given rectangle ____ units²

Area of dilated rectangle _____ units²

Perimeter of given rectangle = 20 units.
Area of given rectangle = 24 units².
Perimeter of dilated rectangle = 100 units.
Area of dilated rectangle = 600 units².

The right triangle below is dilated by a scale factor of 2. Find the perimeter and area of the right triangle below, as well as the perimeter and area of the dilated right triangle. Express your answers as whole numbers, decimals, or fractions in simplest terms (no mixed numbers). Figures are not necessarily drawn to scale.

Perimeter of given right triangle ____ units

Perimeter of dilated right triangle ____ units

Area of given right triangle ____ units²

Area of dilated right triangle ____ units²

Perimeter of given right triangle = 56 units.
Area of given right triangle = 84 units².
Perimeter of dilated right triangle = 112 units.
Area of dilated right triangle = 336 units².

A rectangle with a perimeter of 125 units is the image of a rectangle that was dilated by a scale factor of 4/3. Find the perimeter of the preimage, the original rectangle, before its dilation. Round your answer to the nearest tenth, if necessary.

93.8

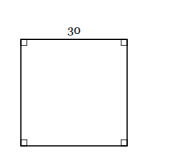
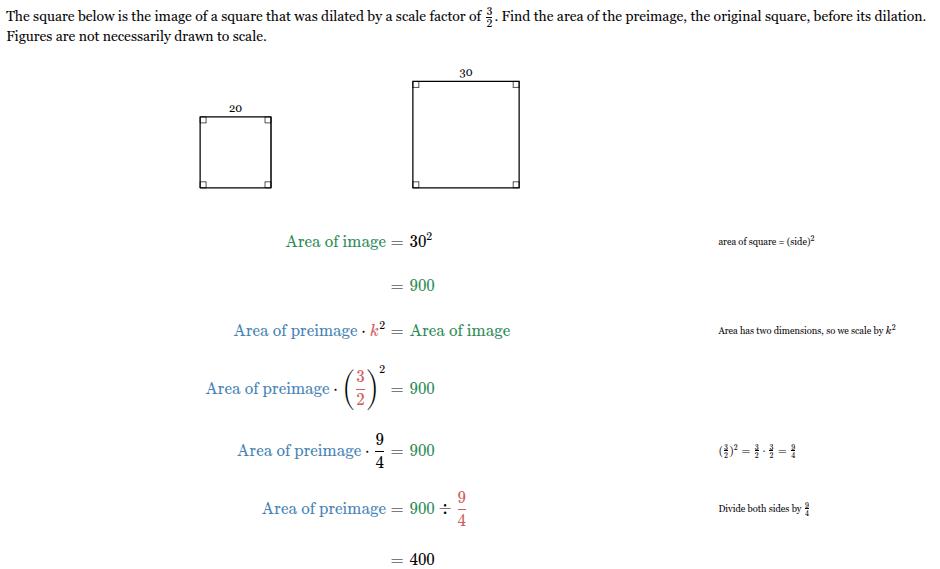
The square below is the image of a square that was dilated by a scale factor of 3/2 . Find the area of the preimage, the original square, before its dilation. Figures are not necessarily drawn to scale.

400

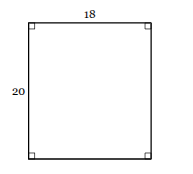
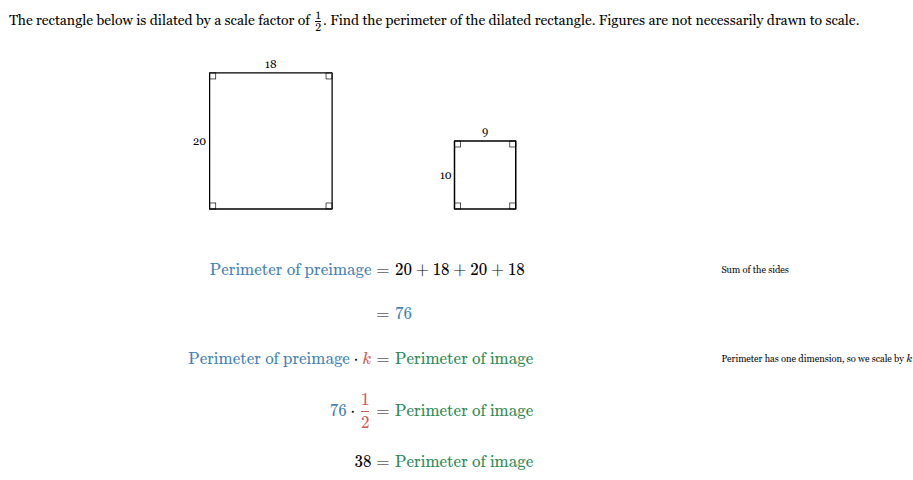
The rectangle below is dilated by a scale factor of 1/2​. Find the perimeter of the dilated rectangle. Figures are not necessarily drawn to scale.

38 units

A rectangle with a perimeter of 133 units is dilated by a scale factor of 1/4​. Find the perimeter of the rectangle after dilation. Round your answer to the nearest tenth, if necessary.

33.3 units

A triangle with a perimeter of 69 units is the image of a triangle that was dilated by a scale factor of 4. Find the perimeter of the preimage, the original triangle, before its dilation. Round your answer to the nearest tenth, if necessary.

17.3 units

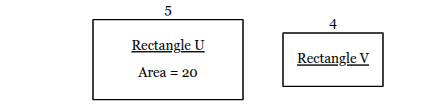
Rectangles U and V are similar. If the area of rectangle U is 20, what is the area of rectangle V?

12.8

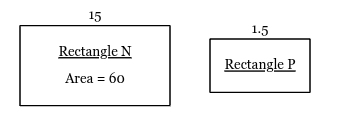
Rectangles N and P are similar. If the area of rectangle N is 60, what is the area of rectangle P?

0.6

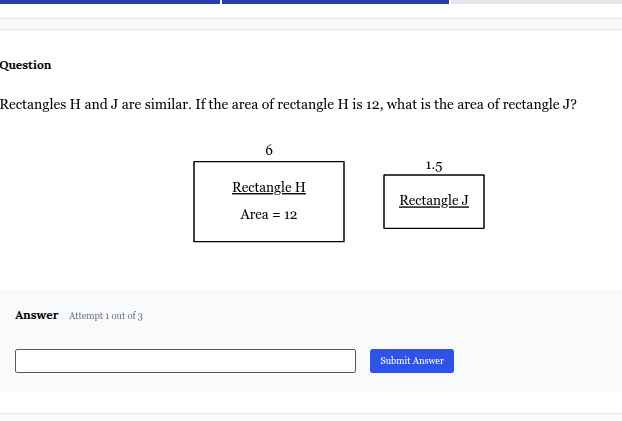
Rectangles H and J are similar. If the area of rectangle H is 12, what is the area of rectangle J?

0.75

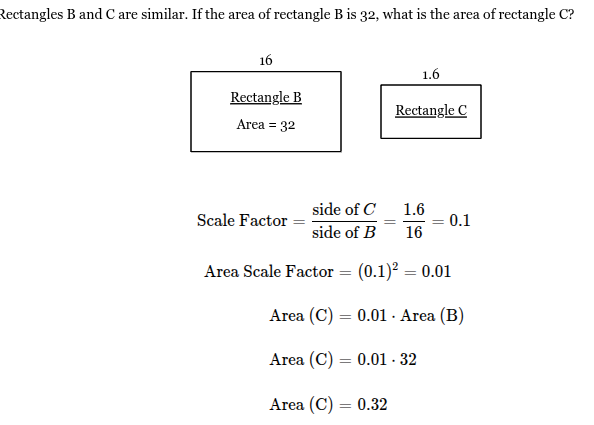
Rectangles B and C are similar. If the area of rectangle B is 32, what is the area of rectangle C?

0.32

Triangle FGH is dilated by a scale factor of 5 to form triangle F'G'H'. Side G'H' measures 85. What is the measure of side GH?

17

Watch VideoShow Examples

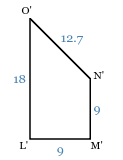
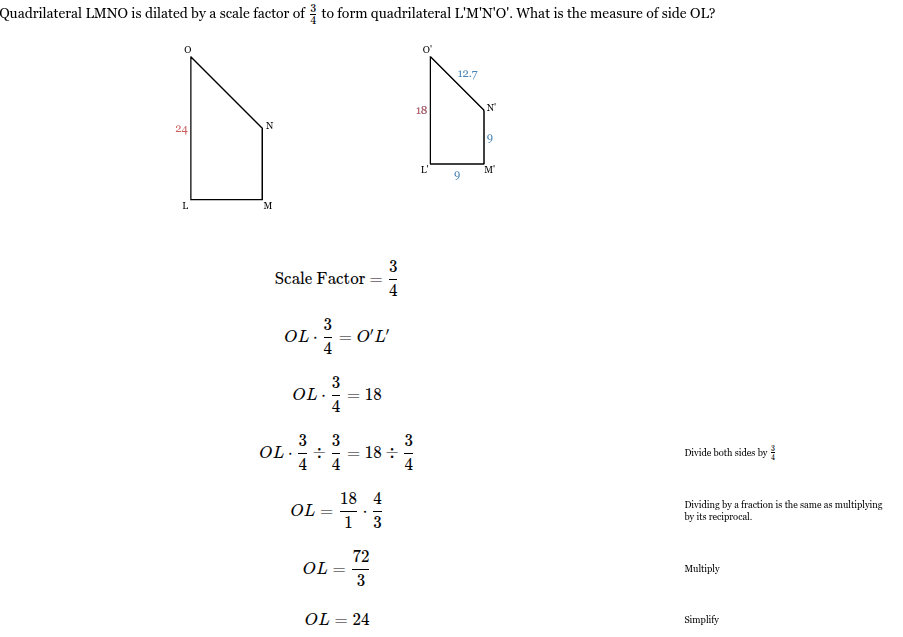
Quadrilateral LMNO is dilated by a scale factor of 3/4 to form quadrilateral L'M'N'O'. What is the measure of side OL?

OL = 24

Triangle QRS is dilated by a scale factor of 1/2 ​ to form triangle Q'R'S'. Side RS measures 35. What is the measure of side R'S'?

17.5

Quadrilateral LMNO is dilated by a scale factor of 2/3​ to form quadrilateral L'M'N'O'. What is the measure of side O'L'?

16

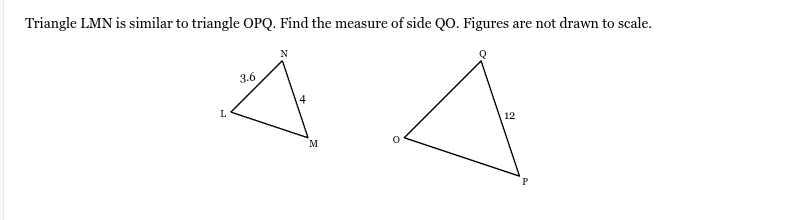
Triangle LMN is similar to triangle OPQ. Find the measure of side QO. Figures are not drawn to scale.

10.8

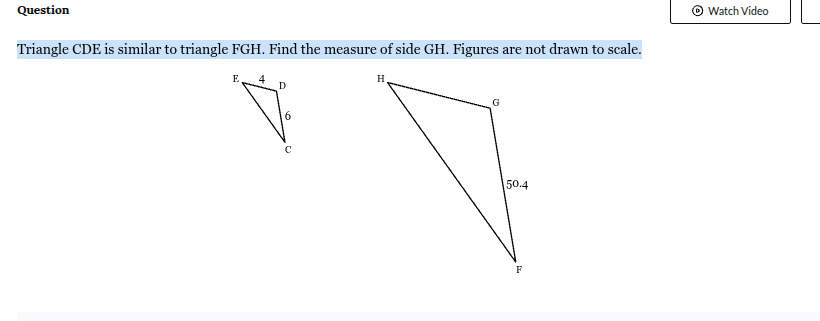
Triangle CDE is similar to triangle FGH. Find the measure of side GH. Figures are not drawn to scale.

33.6

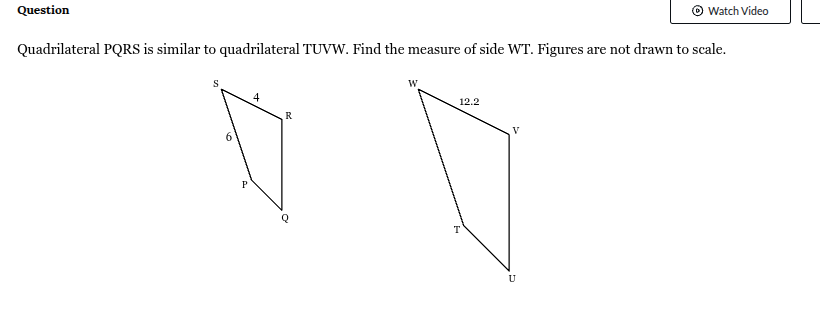
Quadrilateral PQRS is similar to quadrilateral TUVW. Find the measure of side WT. Figures are not drawn to scale.

18.3

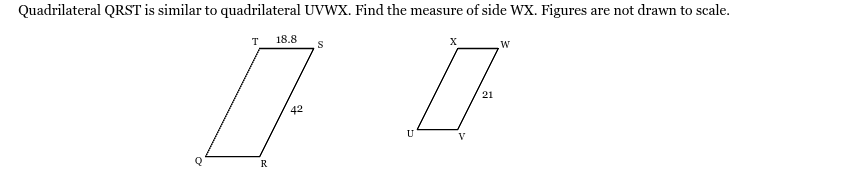
Quadrilateral QRST is similar to quadrilateral UVWX. Find the measure of side WX. Figures are not drawn to scale.

9.4