AP Calculus AB
1/36
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
37 Terms
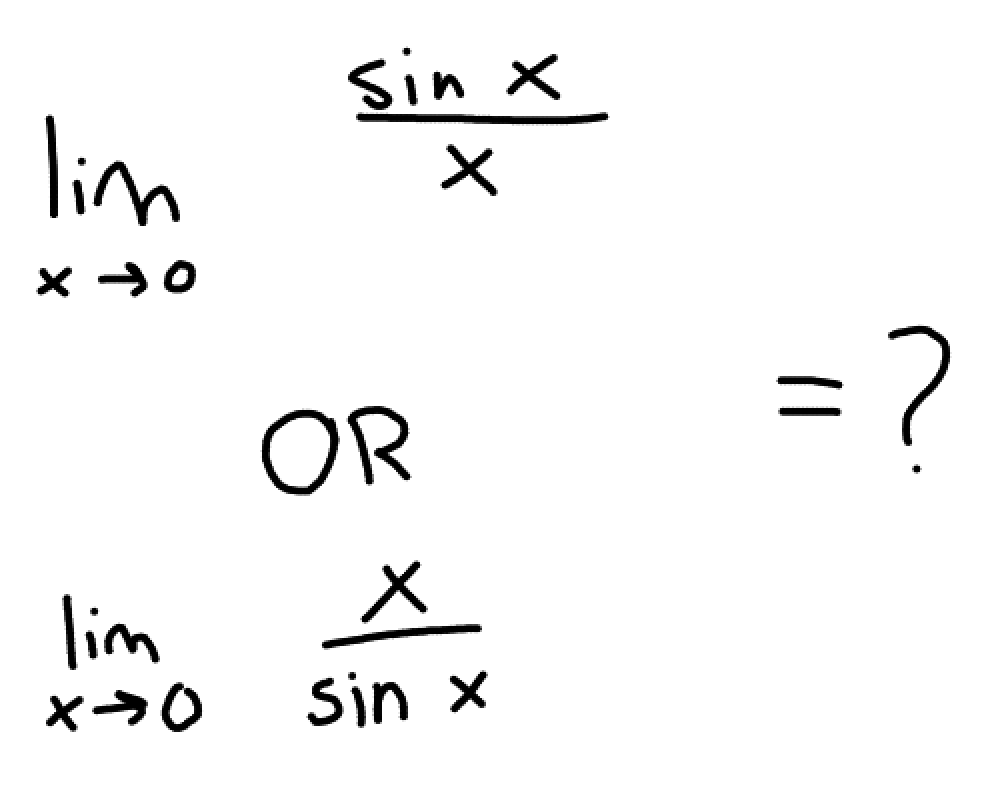
1
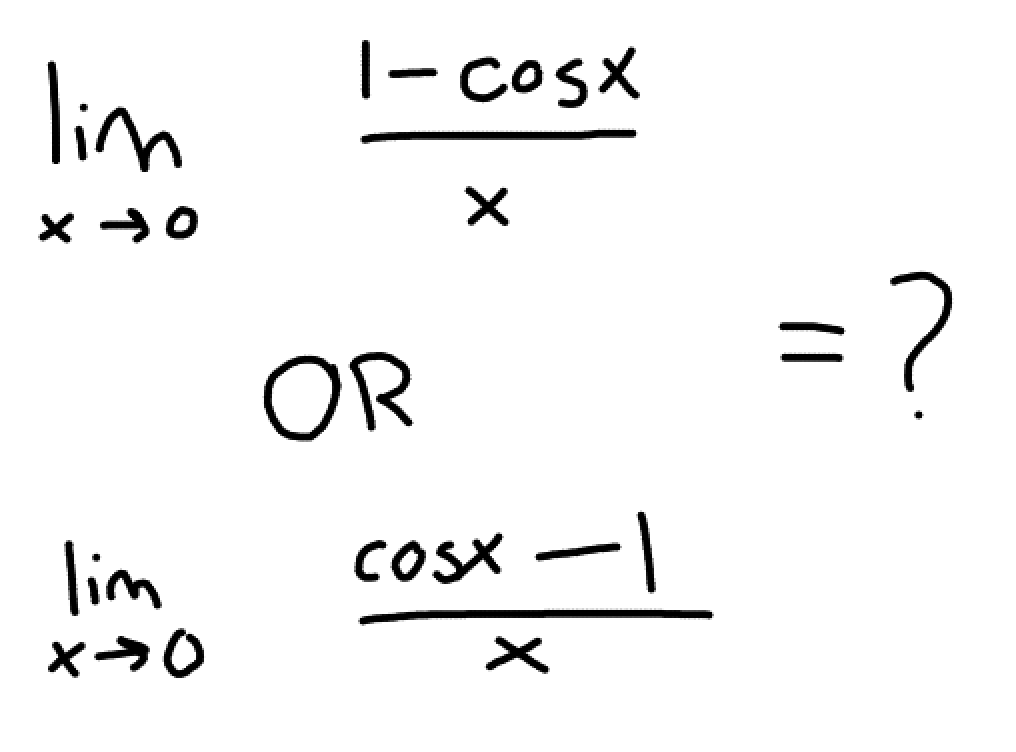
0
In terms of Horizontal asymptotes, if the denominator grows faster the limit is approaching what?
0
In terms of Horizontal asymptotes, if the Numerator grows faster, the limit approaches what?
Infinity or negative infinity
In terms of Horizontal asymptotes, if the numerator and denominator grow at the same rate, the limit is approaching what?
The ratio of their leading coefficients.
For a function to be continuous at x=c, the following 3 conditions must be met:
f( c ) is defined
The limit as x approaches c of f(x) exists
The said limit equals f(c).
What does the intermediate value theorem (IVT) tell us?
This theorum tells us IF f is continuous from a to b, then EVERY value between f( a ) and f( b ) exists at some point within the interval [a,b]
What formula do we use to determine the average rate of change over an interval?
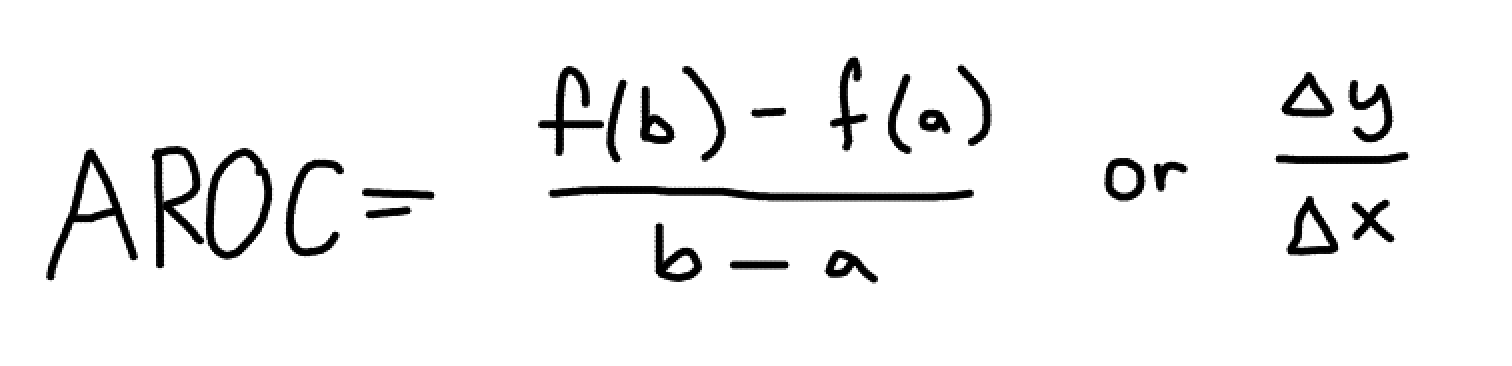
What equation would we use to determine the slope of the secant line?
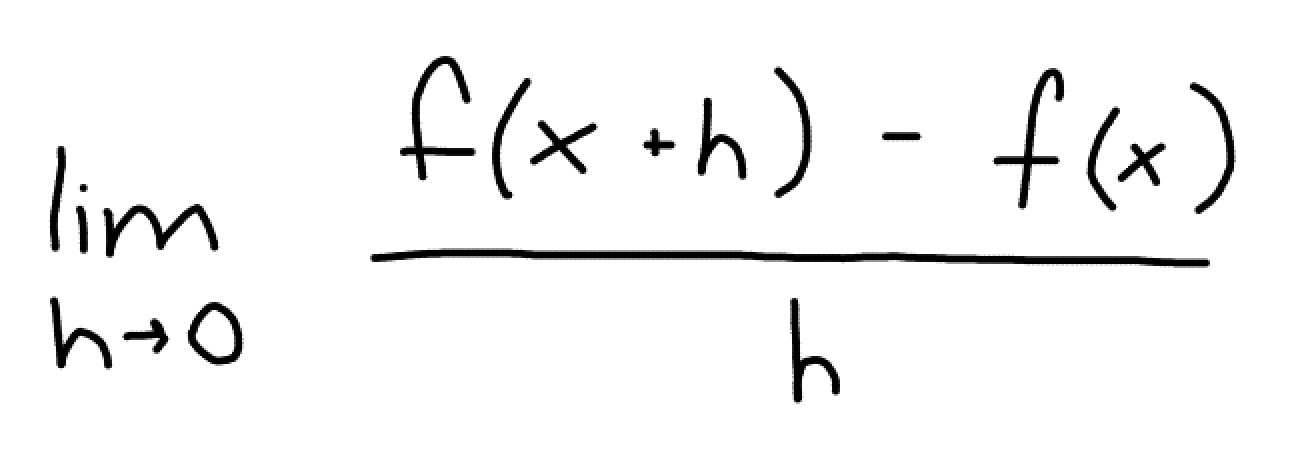
Where would a derivative fail to exist? (3 answers)
At a discontinuity (Hole)
At a corner or cusp (Think the corner of a absolute value function)
At a vertical tangent (Think at (0,0) of a cube root function)
True or false: Differenciability implies continuity
True
True or false: Continuity implies differenciability
False
What does the mean value theorum tell us?
The theorum states if a function f is differenciable (and thereby continuous) over the interval (a,b), then there exists at least 1 point c within that open interval where the instantaneous rate of change (IROC) is equal to the average rate of change (AROC) over the entire interval.
What is the formula for the power rule?
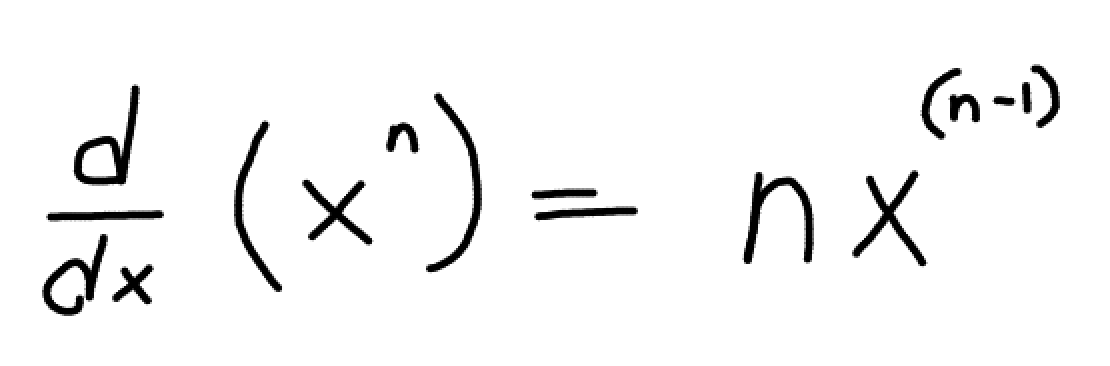
What is the formula for the Product rule?
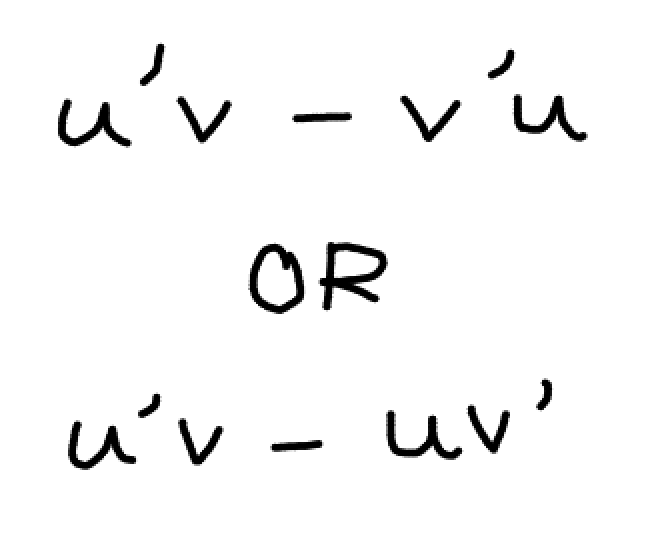
What is the formula for the quotient rule?

What is the difference between a secant line and a tangent line?
A secant line connects 2 points, and is related to AROC
A tangent line touches 1 point, and is related to IROC
What is the derivative of a position graph s(t) ?
Velocity: s’(t) or v(t)
What is the derivative of a velocity graph s’(t) or v(t)?
Acceleration: s’’(t) or v’(t) or a(t)
If the velocity of a particle is negative, what direction is the particle moving?
Left, or downward (depending on what axis the particle is moving on)
When would you use the chain rule?
When you are trying to find the derivative of a function within a fuction

What are the derivatives of these trig fuctions?
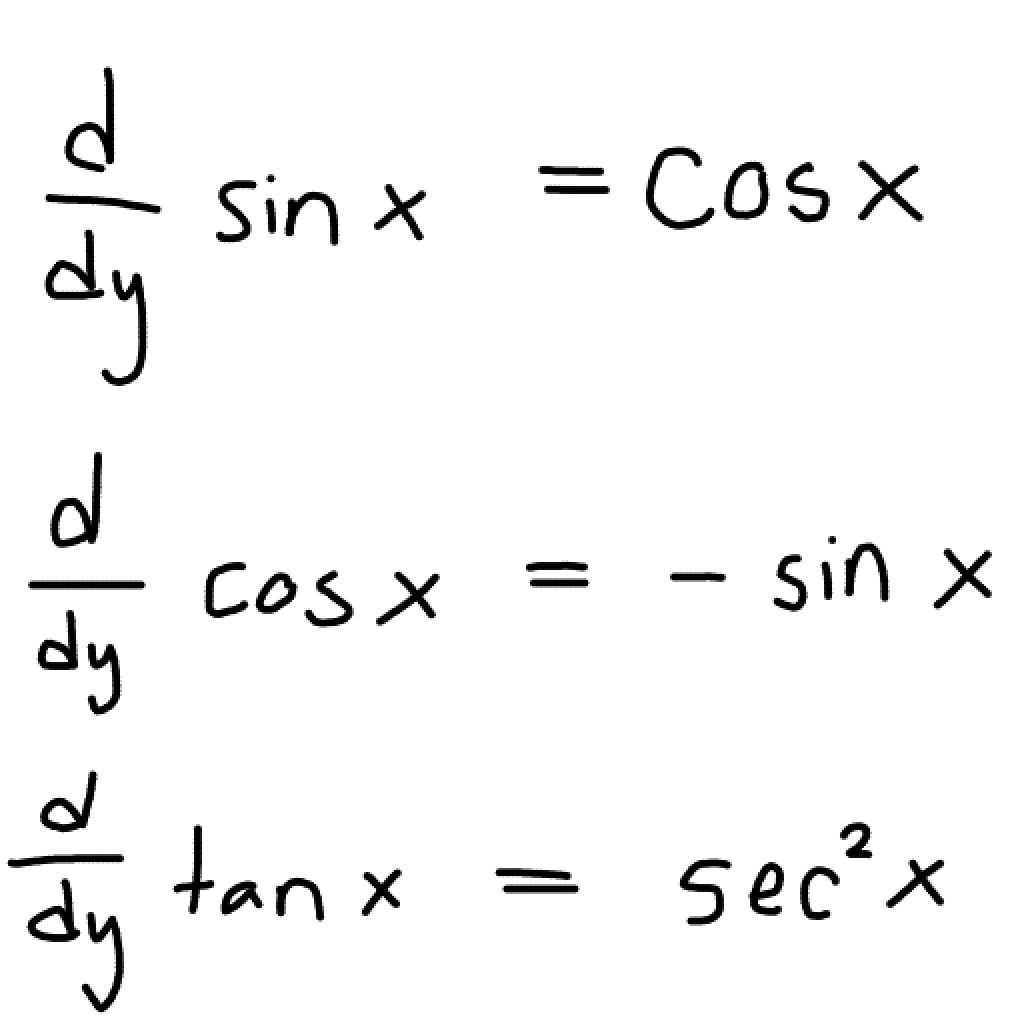
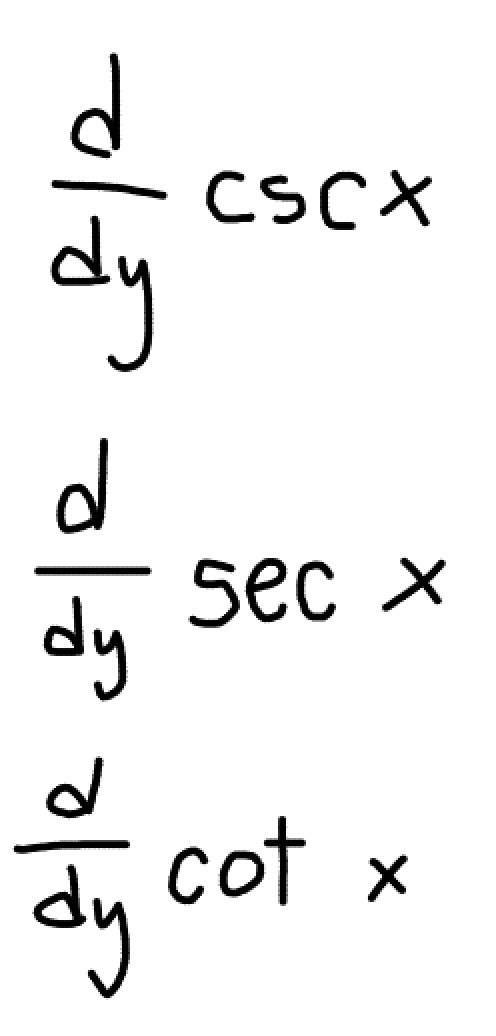
What are the derivatives of these trig functions?
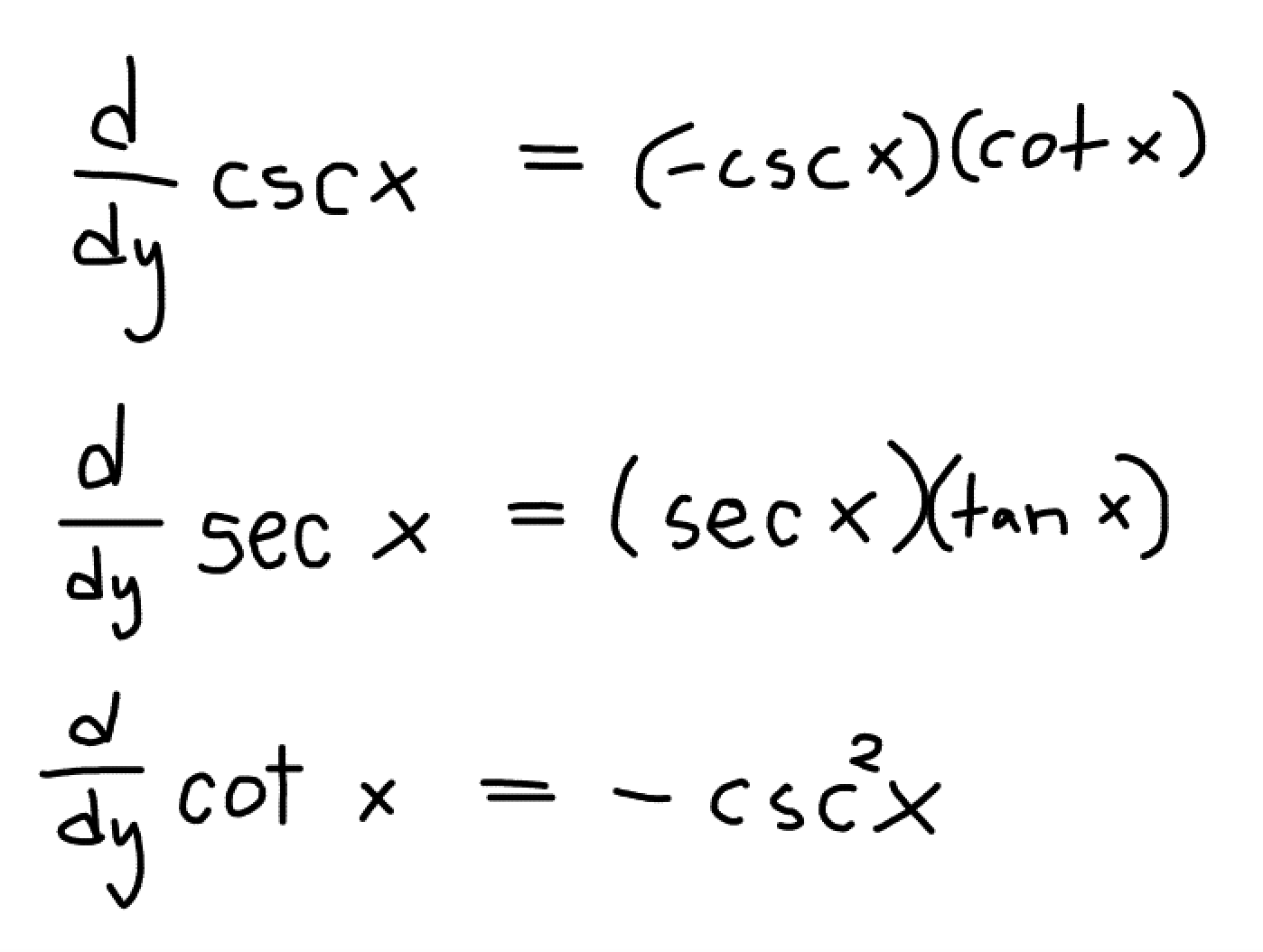
What is the derivative of an exponential function (base e)?

What is the derivative of an exponential function (not base e)?
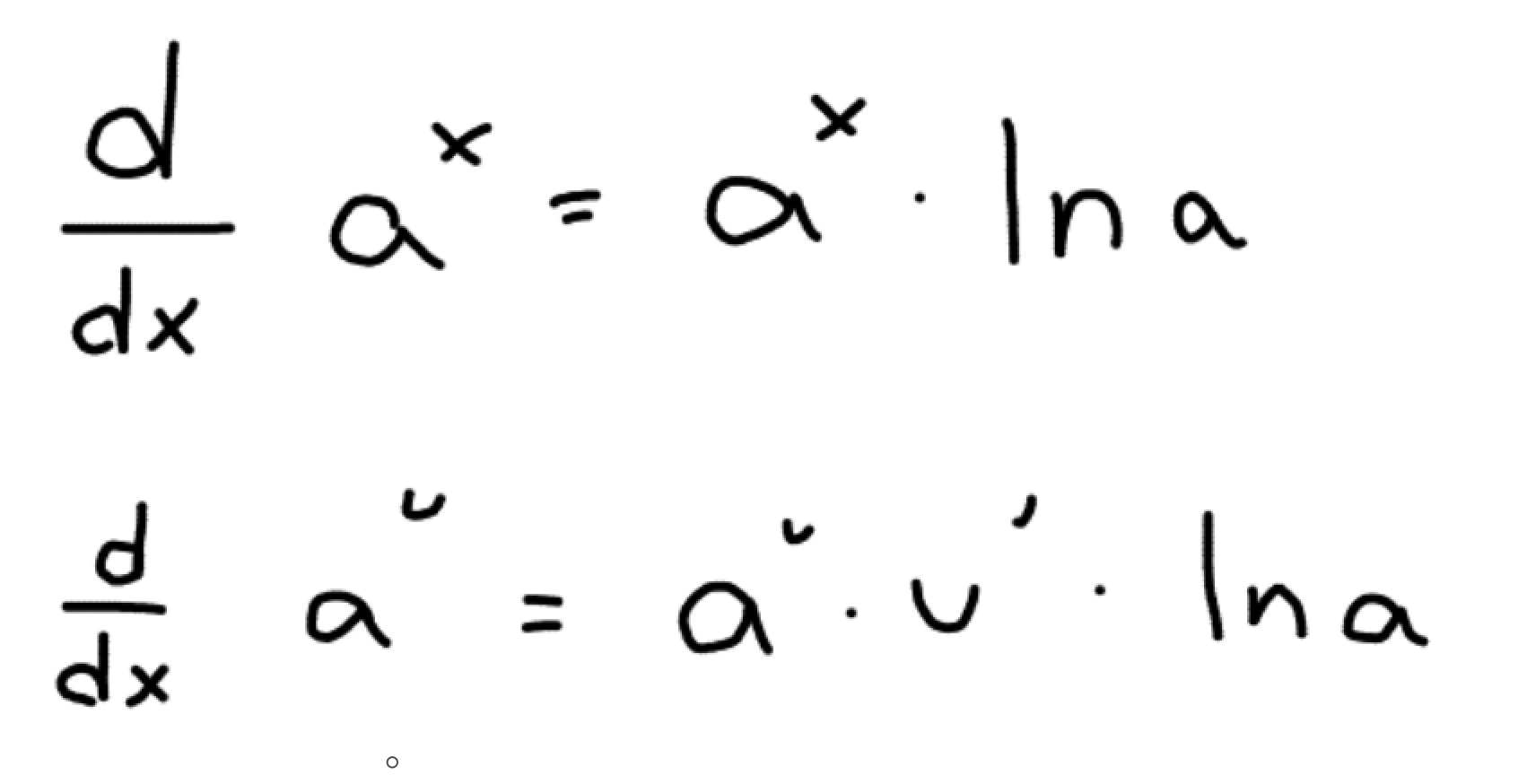
What is the derivative of a natural log function?

What is the derivative of a logarithmic function (not base e)?
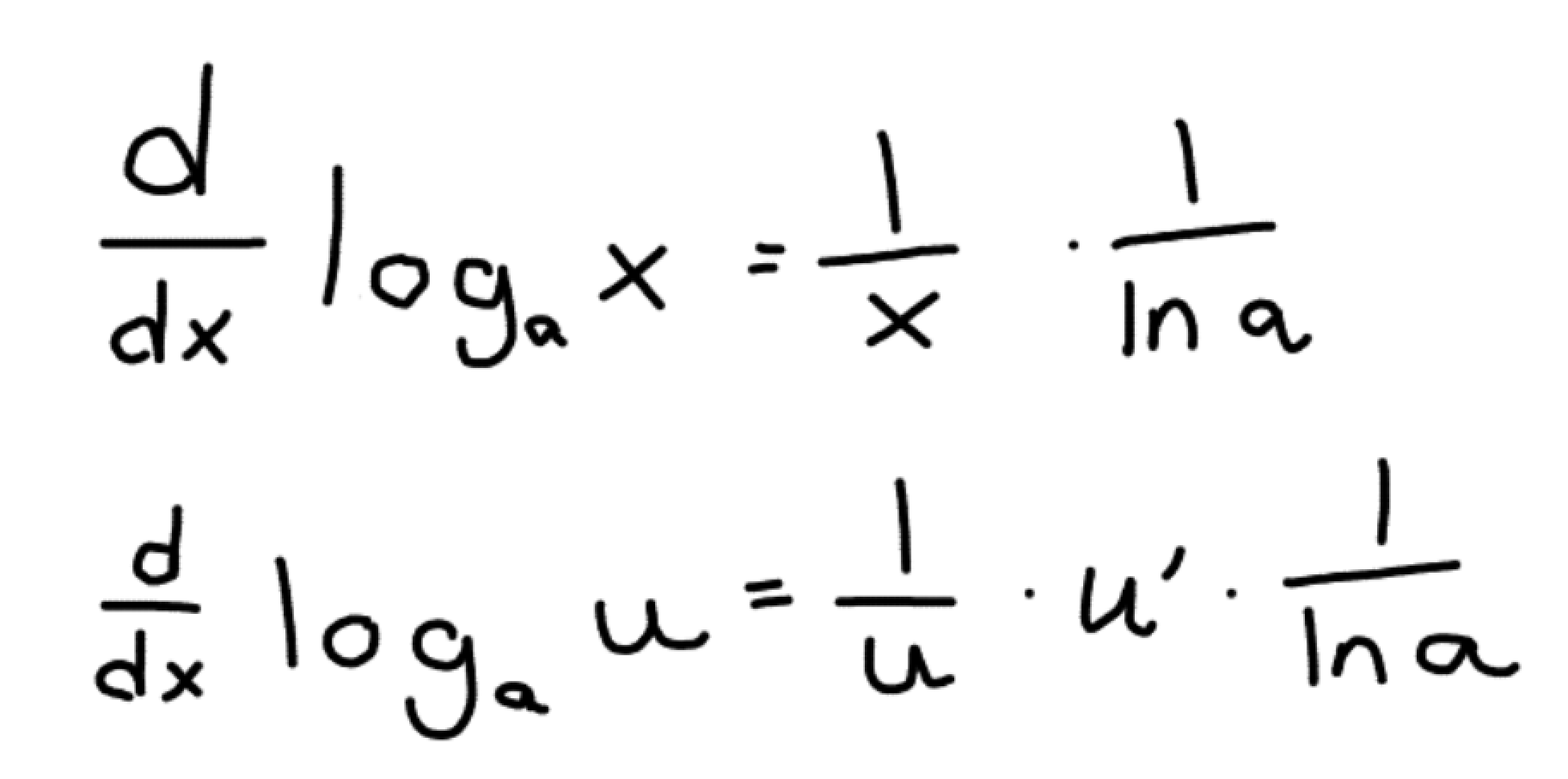

What is the derivative of these inverse trig functions?
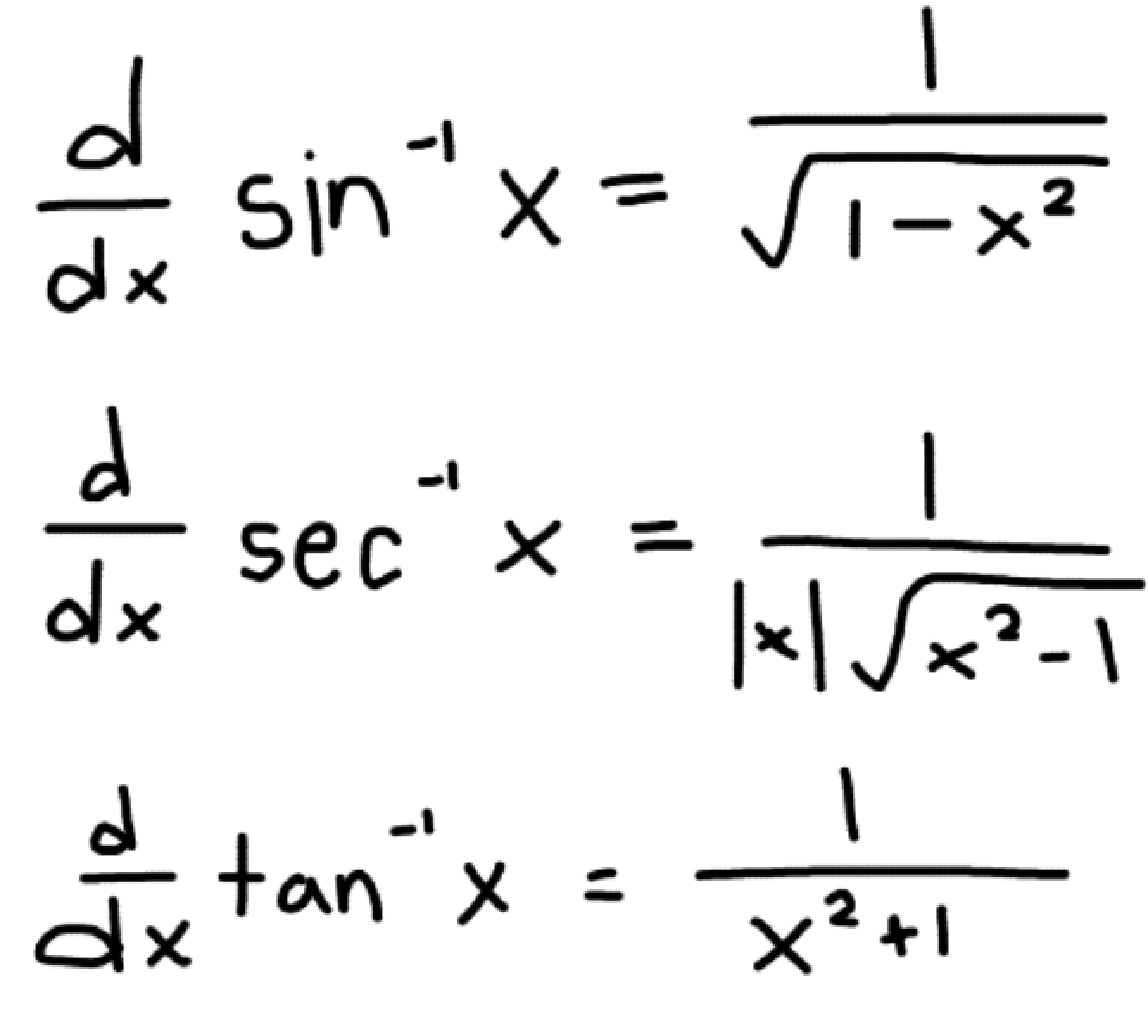

What is the derivative of these inverse trig functions?
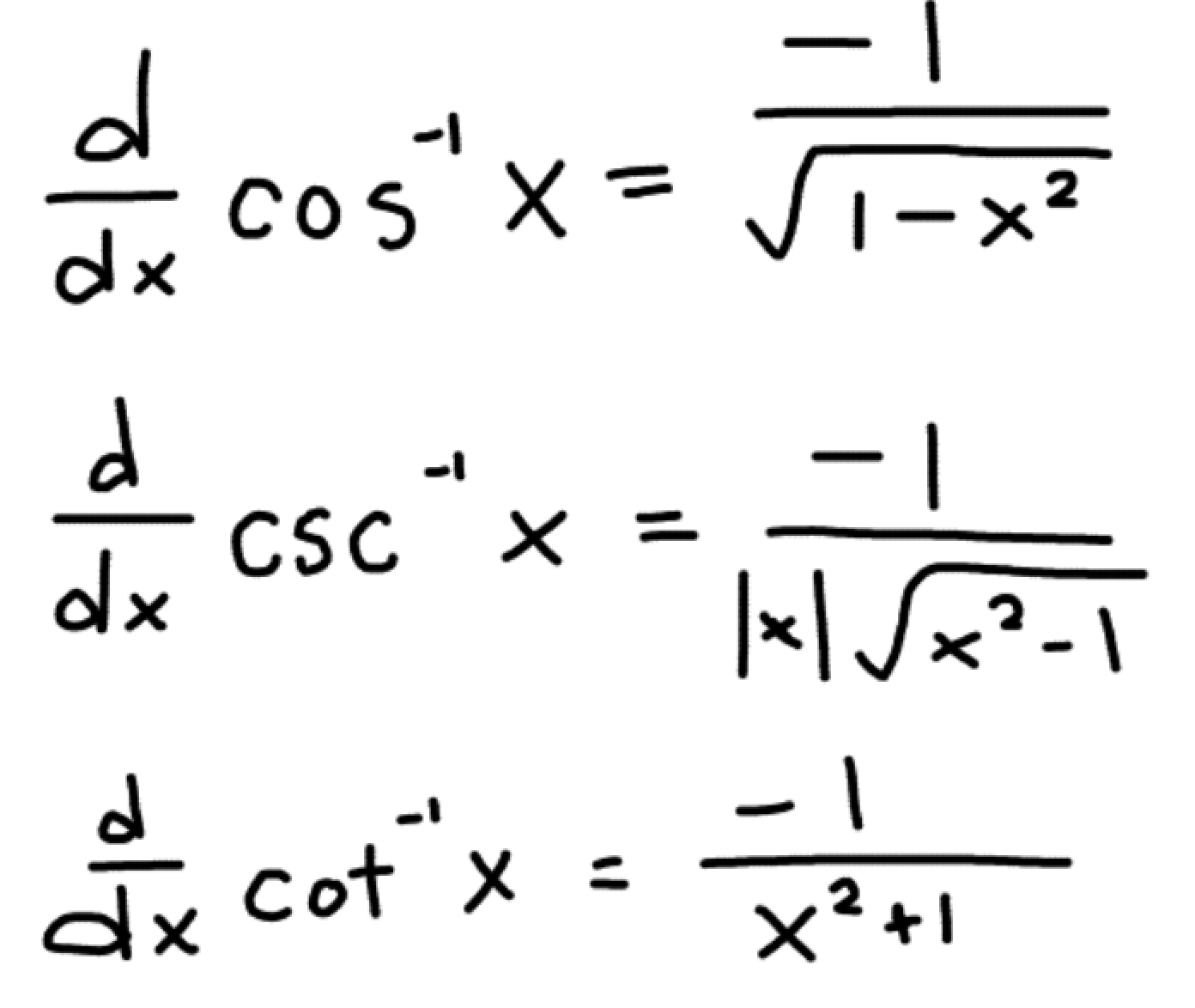
When using direct substitution on a limit and the end result is 0/0 or infinity/infinity, we can use L’Hopital’s rule to do what?
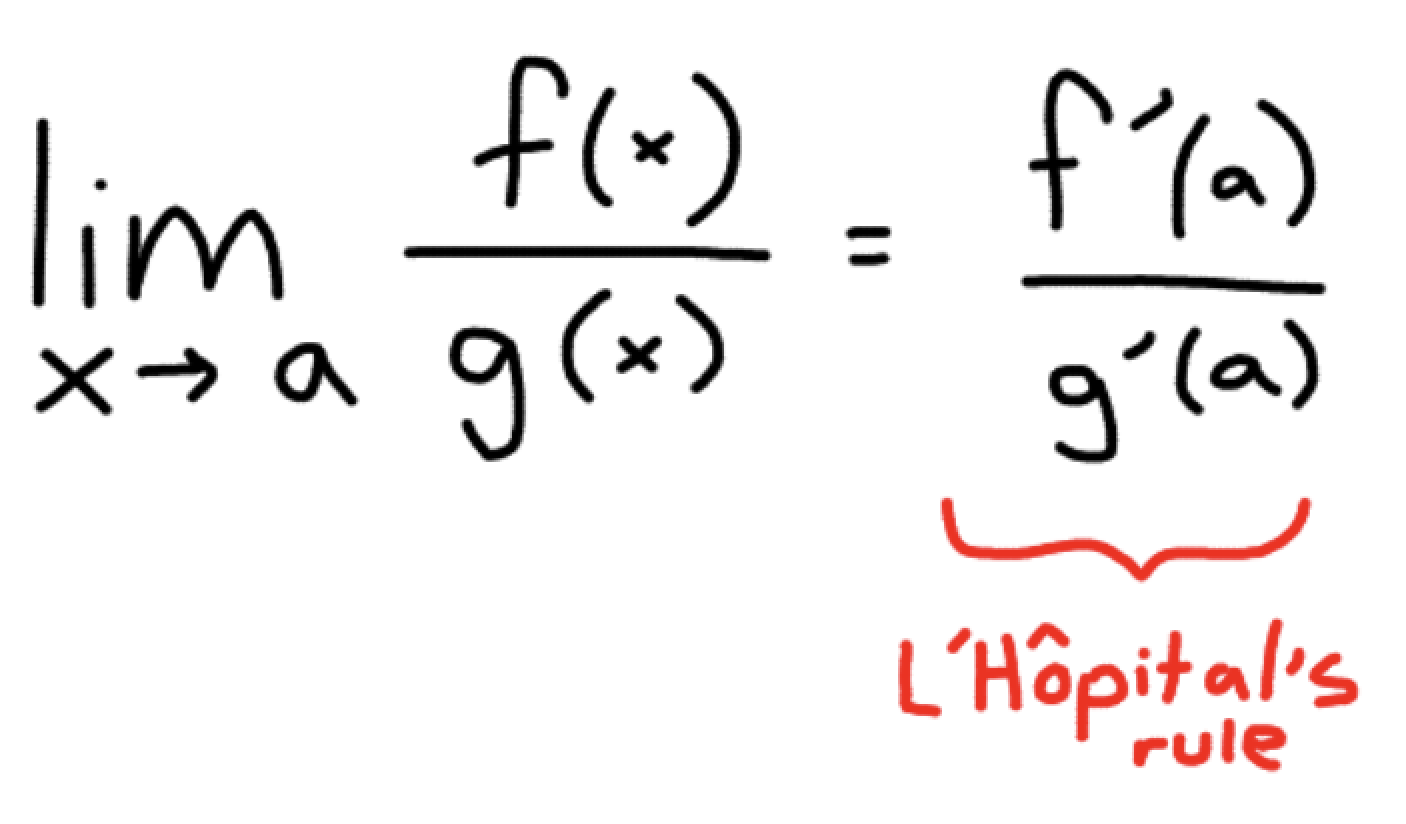
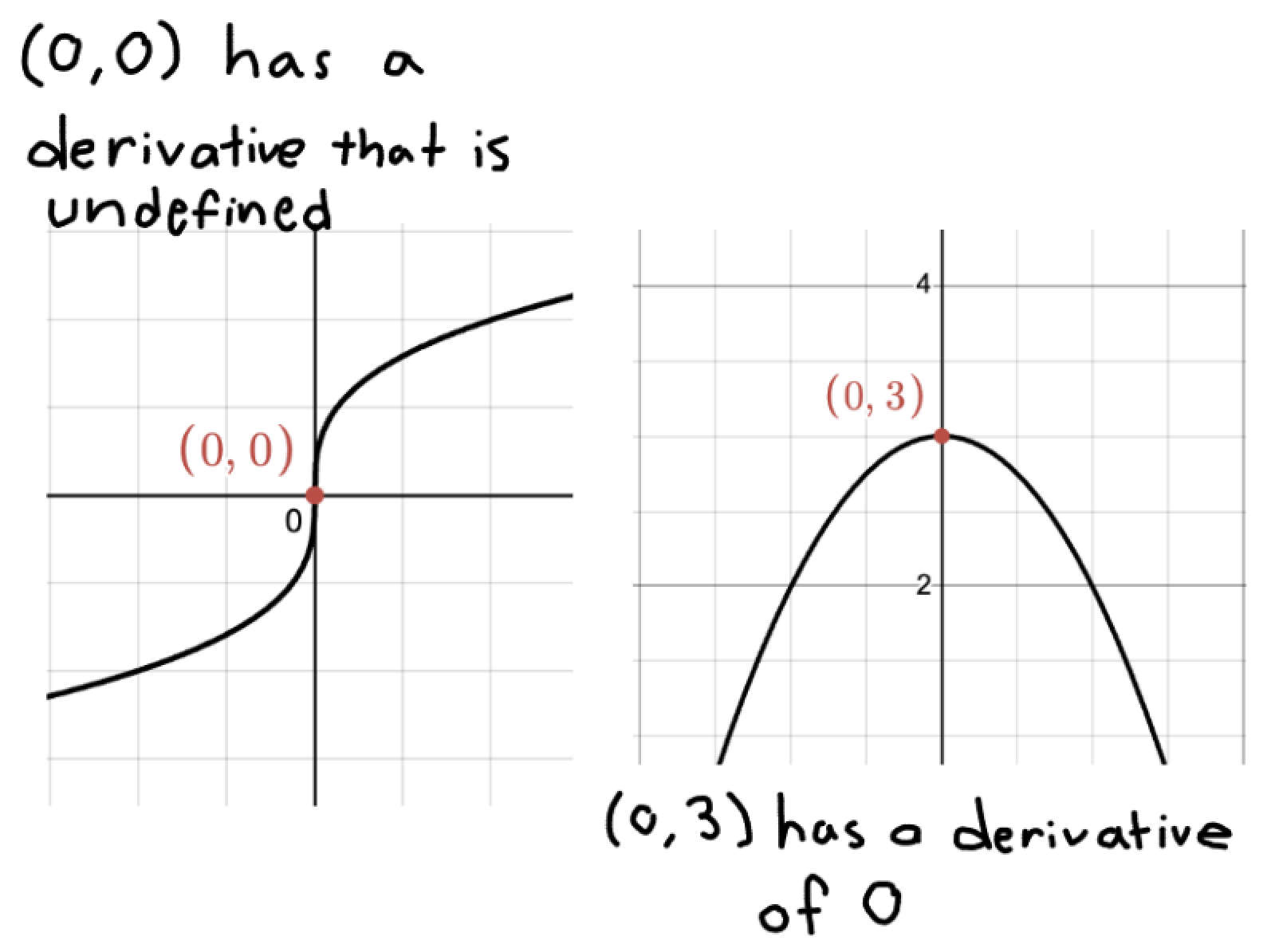
What is a critical point?
When a point on a function has a derivative of 0 or undefined
How do you find critical points of a function?
You find the derivative of the function, and find when that derivative is equal to 0 or undefined.

How do you know if a particle (in a physics question) is speeding up or slowing down?
If the sign (positive or negative) is the same for the velocity AND acceleration, the particle is speeding UP.
If the sign is different between velocity and acceleration, the particle is slowing DOWN.
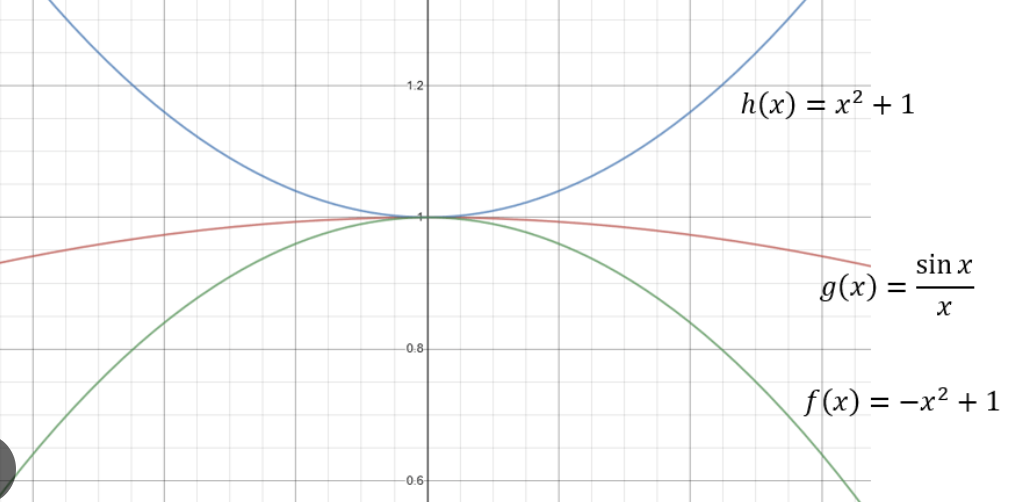
What does the squeeze/sandwich theorum tell us?
If a function, f(x) is “squeezed” in between 2 other fuctions, g(x) and h(x), and both g(x) and h(x) have the same limit as x approaches c, then f(x) must also have that same limit.

How would you format this problem? Make “known” and “find” list. Find the formula you would use to solve this problem (you do not need to differenciate).
Use L for the ladder, B for the base, and Y for the wall.
Formula: b² + y² = 17²

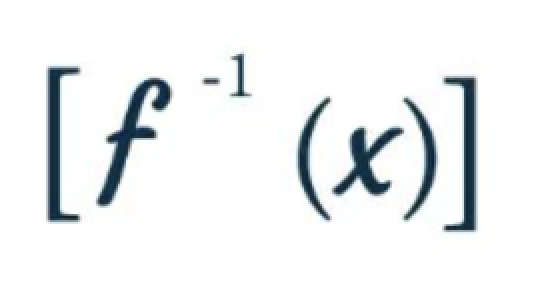
What is the derivative of an inverse function?
1/ f’( f^-1 (x) )

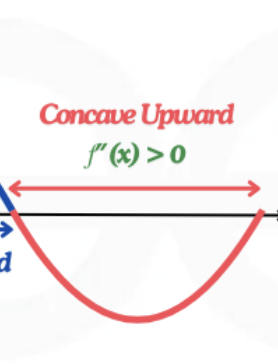
If the second derivative is positive, is the curve concaved up (U shape) or down (n shape)
The curce is concaved up (U shape)