Calc II Chapter 6

Finding the Area Between Curves

1. Draw graph

• Note if there’s two regions because then you will also use A = A1 + A2.

1. Find points of intersection by setting equations equal to each other

2. Double check validity of points by plugging it back in to eqn made in Step 1

3. Solve for area using

4. Use points of intersection as bounds

5. Integrate

Graph of Sinx

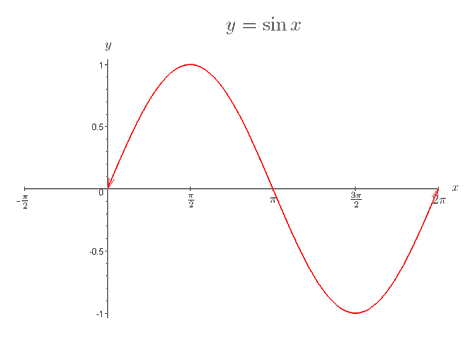
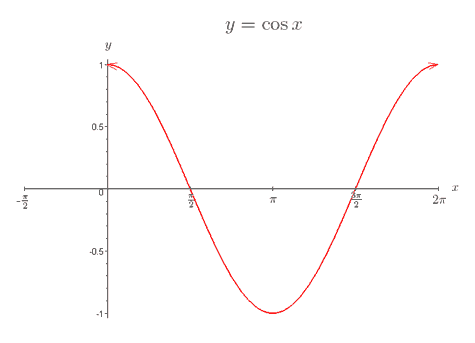
Graph of Cosx

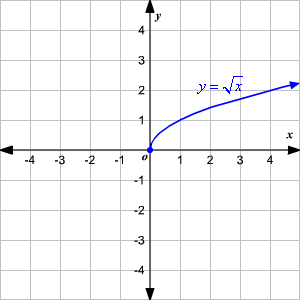
Graph of sqrtx

Finding Volume Doing Slicing

1. Draw the graph

• Note that x^2 + y^2 = r^2 is a circle. So if you have x^2 + y^2 = 9, then this is a circle with 3 radius

2. If needed, solve equation for y

3. Use the formula

4. Find the formula of the slice’s shape

   Square = s^2

   Equilateral triangle = (sqrt3/4)(s^2)

   Semicircle = 1/2 pi r^2, r = 1/2s

   s is top - bottom

5. Put +/- radius as integral boundaries

6. Integrate

Finding Volume with Solids in Revolution

1. Decide method of washers (disks)  or cylindrical shells and use to solve

Methods of Washers

perpendicular to axis of rev

1. Draw graph

2. Draw slice perpendicular to axis of rev

3. Find thickness (if needed, convert equns wrt to x or y depending on thickness)

4. Find R (distance between axis of rev and farthest graph)

5. Find r (distance between axis of rev and closest graph)

6. Find points of intersection by setting eqns equal to each other

• these are the integral bounds

7. Plug everything into formula

Note that R and r with just be the line of the closest or farthest equation if the axis of revolution is just x/y axis or 0

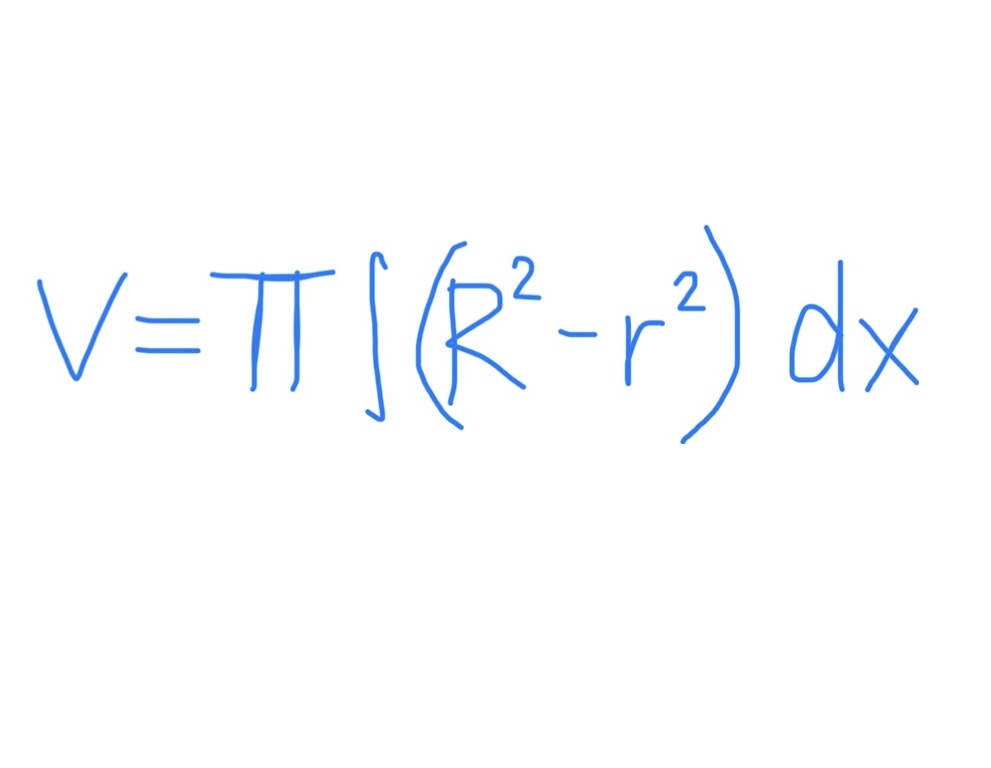
Method of Shells

parallel to axis of rev

1. Draw graph

2. Draw slice parallel to axis of rev

3. Find thickness

4. Find r (distance between axis of rev and midpoint of slice)

5. Find h (top - bottom)

6. Find points of intersection by setting eqns equal to each othe

• these are integral bounds

7. Plug into formula

Note: Midpoint of slice is normally just x

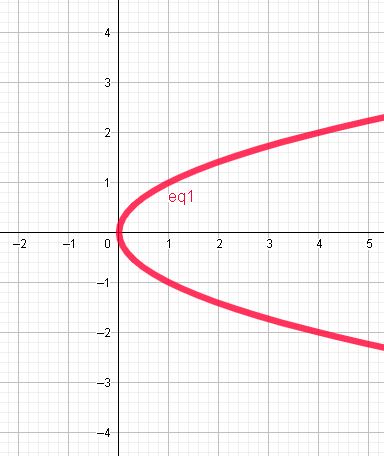
Graph of x = y^2

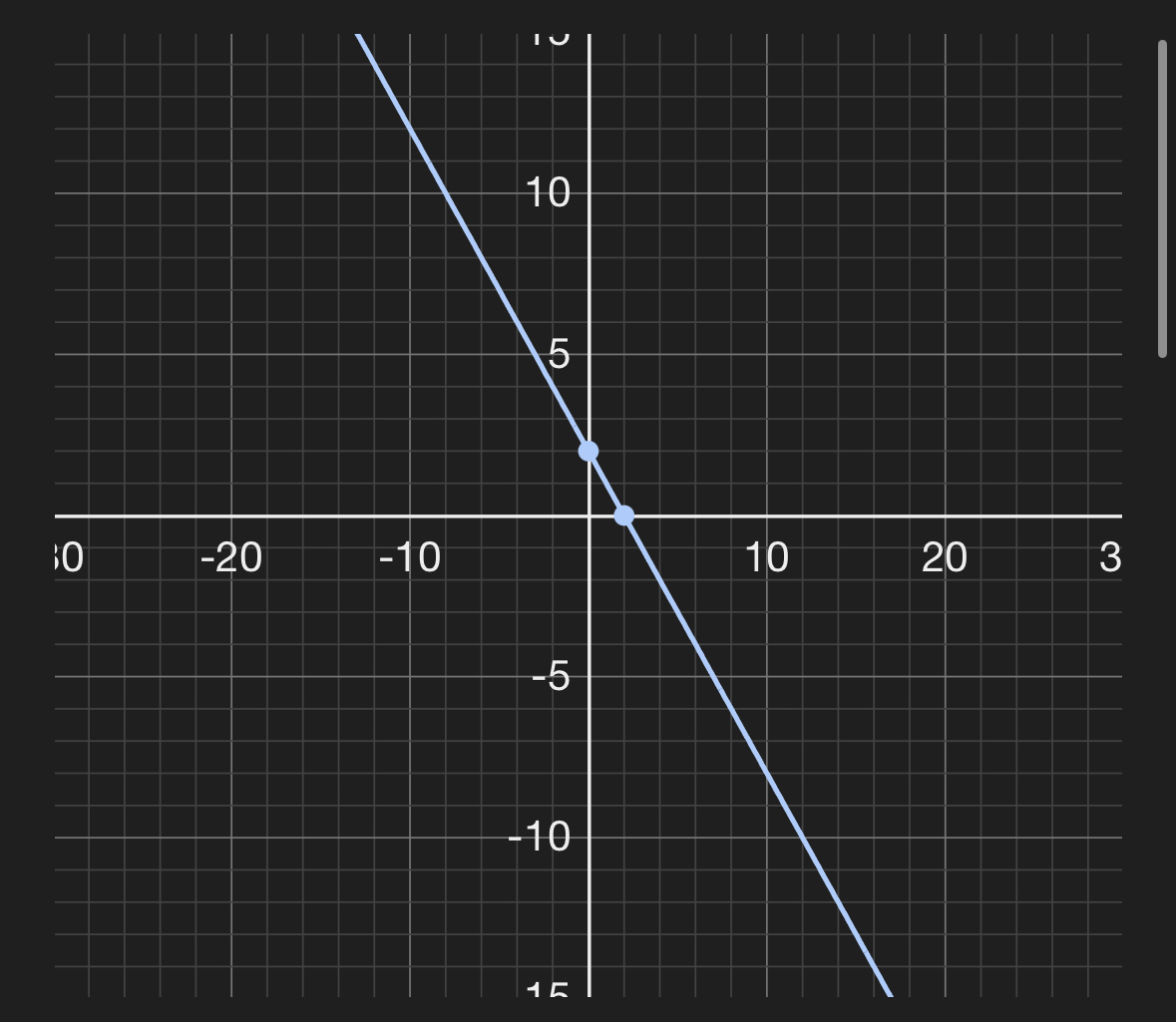
Graph of 2-y

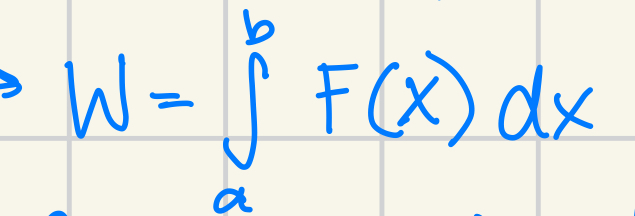
Finding Work if Force Isn’t Constant

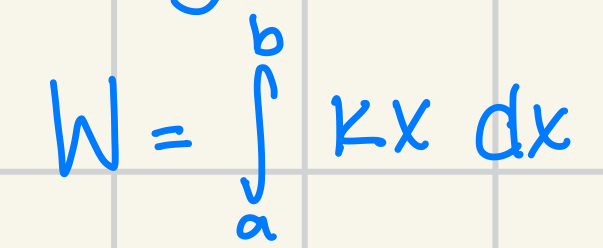
Finding Work for a Spring

1. Find k which is the spring constant using F = kx solving for k

2. Create integral

   • b: initial length - natural length

   • a: new final length - natural length

Note: x is distance beyond natural length, k is spring constant

Finding Force of a Fluid

1. Draw picture and draw slice

2. Set up formula

3. Plug in density

4. Plug in L which is length of slice

5. Plug in depth which is height - y or depth - y

6. Plug in integral b and a

• b: depth of fluid

• a: 0

Formula for