COMP 211: Lecture 6 - Information Encoding, Number Systems, and Integer Representation (and Character Encoding)c

What do humans understand?

Numbers and strings (i.e characters)

What are examples of what humans understand?

100 or the matrix

What do machines understand?

Binary numbers

Do machines understand human language?

No. We have to convert human language into binary representation

What is encoding?

To convert information into a different form.

What is a character example of binary encoding?

‘a’ encoded as binary 01100001_2 number

What is the representation for transforming characters to binary?

ASCII representation

What is a number example of binary encoding?

25_10 encoded as 00011001_2 number

What is the representation for transforming numbers to binary?

Base-2 representation

How many digits do base-10 numbers have?

10; 0-9

What does it mean for a number to be base-10?

Each digit is multiplied by a power of 10

What is the formula for getting to base-10?

v is base-10 value, d is decimal digit, and i is digit position, increasing right to left, starting from 0

• How do we get 17543_10?

• How do we get 173_10?

• How do we get 1025_10?

• How do we get 2001_10?

Answer

What are base-2 numbers?

Binary numbers

How many digits to base-2 numbers have?

2 binary digits; 0 and 1

What does it mean for a number to be base-2?

Each digit multiplied by power of 2

What is the formula for getting to base-2?

v is base 10 value, b is binary digit, and i is digit position

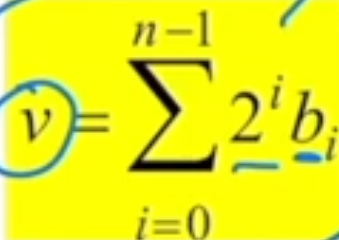
What is the range of binary numbers?

0 - (2^N-1)

N = Number of bits

• How do we get 011111010000_

• How do we convert 73_10 to binary?

• How do we convert 181_10 to binary?

• How do we convert 213_10 to binary?

• 2000_10

• 01001001

• 10110101

• 11010101

What are some Base-2 Terminology?

LSB, MSB

What is LSB?

Least significant bit

What is MSB?

Most significant bit

What is considered the least significant bit? What is considered the most significant bit?

The LSB is going to be the lowest power of two, and the MSB is the highest power of 2

What is the goal of a Decimal to Binary Algorithm?

We can apply a more algorithmic approach to converting a base-10 decimal number to binary; inverse problem

What is the Decimal to Binary Algorithm?

Where does the Decimal to Binary Algorithm Apply?

To any other number bases

How do we use the Decimal to Binary Algorithm on other number bases?

for base-n, replace divide by 2 with divide by n

• Convert 18_10 to binary (base-2)

10010

What are Base-16 numbers also called?

Hexadecimal numbers

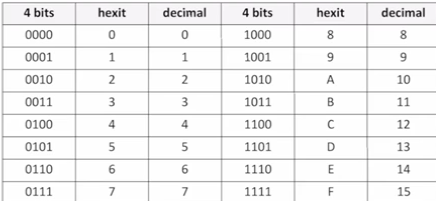
How many digits are in hexadecimals?

16 hex digits; 0-9 and A-F

What is a hex digit also called?

Hexit

What is a hexdigit?

A group of 4 binary bits

What is each hexit multiplied by?

A power of 16

WHat is the formula for hexits?

v is base-10 value, d is hexit, and i is digit position (increasing right to left, starting at 0)

• 0×7d0

• Convert 73_10 to Hexadecimal

• Convert 01101100_2 to Hexadecimal

• Convert 0xA9 to Binary

0111 1101 0000

0049

6C

1010 1001

What is ASCII?

A standard format with 7 bits encoded to 128 characters

How many characters total in ASCII?

2^7'

• ‘A’ in base_10, base_2, and base_16

• ‘0’ in base_10, base_2, and base_16

• ‘\0’ in base_10, base_2, and base_1

65; 1000001; 0×41

48; 0110000; 0×30

0; 0000000; 0×00

What character has a 0 value?

The null terminator

Why is the null terminator value important?

Because it’s the only character with 0 value, it allows us to null terminate strings (recognizes the end of a string)

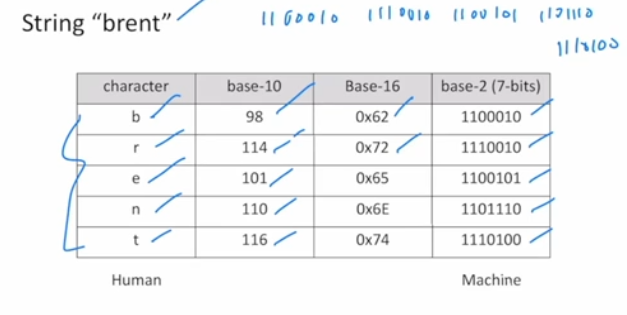
• Convert ‘brent’ to Binary

What is fixed-length encoding?

When all symbols have same number of bits

What is an example of fixed-length encoding?

ASCII; each character always has 7 bits

When is fixed-length encoding used?

When all symbols have equal probability

What is variable-length encoding?

When symbols can use different numbers of bits

What is an example of variable-length encoding?

UNICODE 8 and 16

When is variable-length encoding used?

When some symbols are more likely than others; for example, compression

Variable-length Example

• Suppose X and Y are twice as likely as W and Z

• Encoding possibility: X and Y are 1 bit, W and Z are 2 bits

• X and Y would use less bits, while W and Z require more bits

• Main concept is commonly occurring symbols are encoded with few bits; the idea behind compression

How do we determine the number of bits for fixed-length representation?

• Number of symbols = to 2^ number of bits

• if we had 2 symbols, one bit is needed

• If we had 4 symbols, 2 bits are needed

• If we have 2^n symbols, then n bits are needed

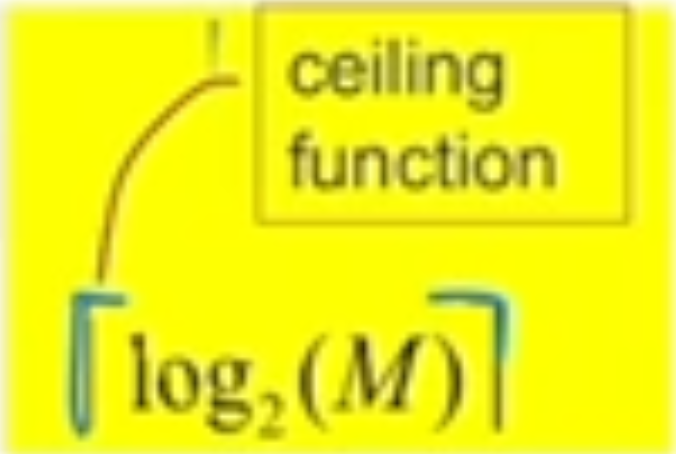
  • We take the ceiling of log_2(M) to find number of bits for M symbol==

• If we had the digits {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, how many bits are need?

• If we had the 84 english characters (A-Z (26), a-z (26), 0-9 (10), punctuation (8), math (9), financial (5)), how many bits are need?

log[10] = 3.22 → 4

log[84] = 1.92 → 2

What is MSB used for? How?

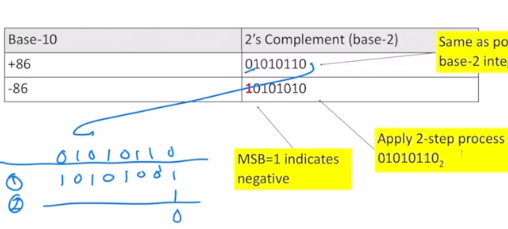
Used to encode the sign. If MSB = 0_2, then it is a positive binary number. If MSB = 1_2, then it is a negative binary number.

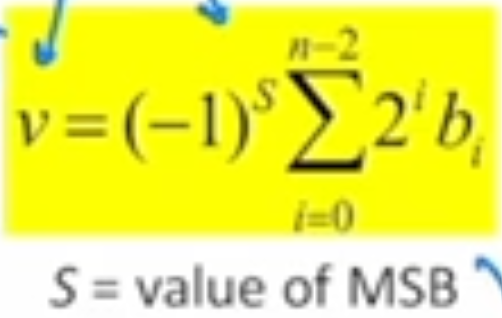
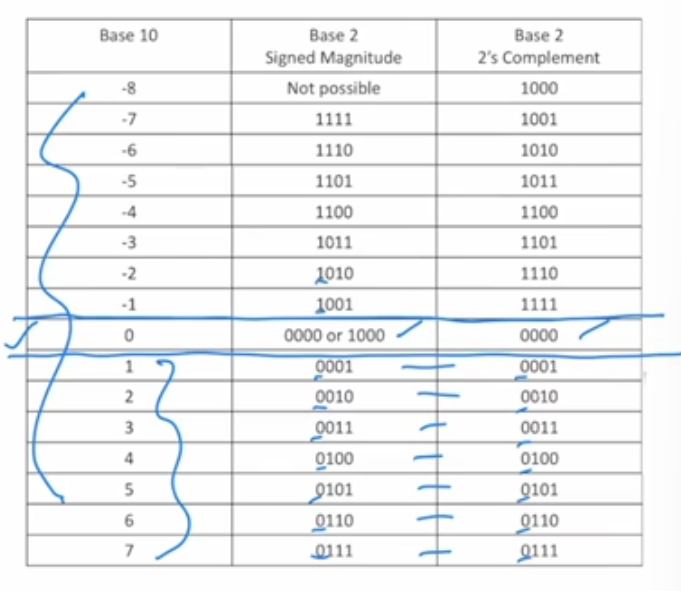
What is the range for Signed Magnitude Representation?

-(2^(N-1) - 1) to (2^(N-1) - 1)
N = # of bits

What is the range represented in?

Base-10

If N = 8 bits, what is the minimum base-10 number that can be represented in signed magnitude? What is the maximum base-10 number

-127 - 127

1. What is -49 in SMR

2. What is +49 in SMR

3. What is +86 in SMR

4. What is -86 in SMR

10110001

00110001

01010110

11010110

Why is Signed Magnitude Good?

Easy to negate and compute the absolute value.

What is one reason why Signed Magnitude is bad?

Adding and subtracting can become complicated because we would need to implement a first hardware circuit to the add, and a second hard ware circuit to subtract.

What is the second reason why Signed Magnitude is bad?

2 different ways to represent 0. If all the bits are 0 and the MSB is 1, then the number is a -0. If the MSB is 0, then it is +0. Being able to represent 0 in 2 different ways is not ideal because it can complicate hardware design

What is signed representation like in practice?

It is not frequently used for integer numbers, but used in floating point numbers.

What is another signed representation?

2’s Complement Representation.

How is the sign encoded in 2’s Complement?

MSB is used, so 1 = negative sign, and 0 = positive sign. Conversion from base-10 to base-2 is slightly different from standard MSB Signed magnitude.

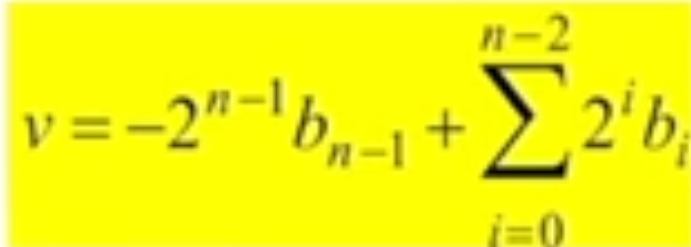
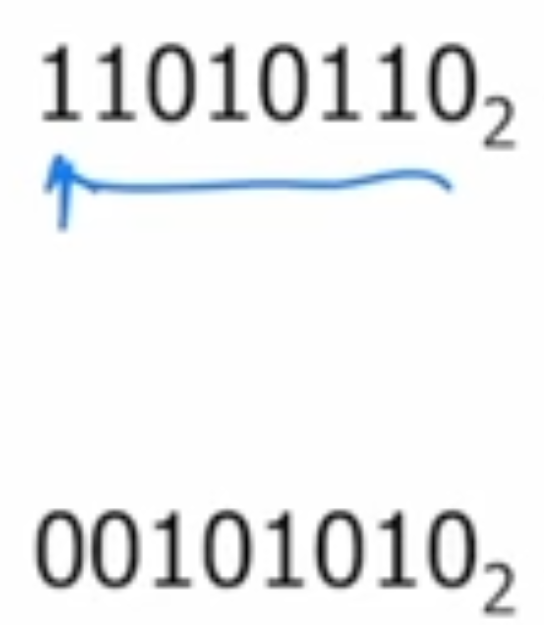
2’s Complement examples

-42

42

What is another process other than the formula to convert base-10 to base-2 in 2’s Complement?

A two step negating a number and algorithmic approach.

Explain the 2’s complement second approach.

1. Complement every bit (1_2 → 0_2, 0_2 → 1_2)

2. Add 1_2 using binary math (see supplement reading assignment)

2’s Complement Example

Answer

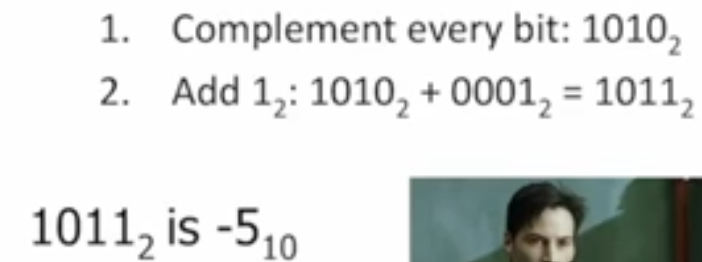
1. +86 to 2’s Complement

2. -86 to 2’s Complement

What is 2’s complement’s range?

(-2^(N-1)) to (2^(N-1) - 1)

If N = 8, what is the range in 2‘s complement?

Answer

What will happen if you apply 2’s complement to a negative number?

You will get a positive number.

Apply 2’s Complement to this negative number.

What is another thing we can do in 2’s complement? Why?

Addition, no subtraction. Because we use the MSB to determine whether the number is negative or not, we could do the number + a negative number to perform subtraction.

What is a good thing about representing integers in 2’s Complement?

There is only one 0, no positive or negative 0.

Prove the claim about the 0 in 2’s complement.

Answer

Signed Magnitude vs 2’s Complement

Sign Extension Example.

We would pad the MSBs with 0s to make 8. We don’t change the value of the number.

What do we do if we wanted sign extension with a negative binary nmber?

We would need to use 2’s complement, signed magnitude does not work.

What is the bad things about 2’s complement?

More complex to negate and compute the absolute value.

What are all the good things about 2’s complement?

2’s complement fixes the issues with signed magnitude. It uses only the add operation, only has one 0, and can use sign extension. Overall, it simplifies hardware design.