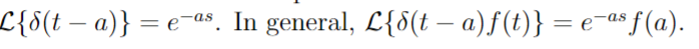Differential Equations Exam 3

Linear Equations of order n

yⁿ(x) + p₁(x)y⁽ⁿ⁻¹⁾(x) + · · · + p_n(x)y(x) = g(x)

Existence and Uniqueness Theorem

If the coefficients are continuous on (a, b) and
x₀ ∈ (a, b), there is a unique solution y(x) on (a, b) satisfying y(x₀) = y₀, y′(x₀) = y′₀, ... , y⁽ⁿ⁻¹⁾(x₀) = y⁽ⁿ⁻¹⁾₀ , for any given initial values y₀, y′₀, ... , y⁽ⁿ⁻¹⁾₀

Linear Differential Operator

Dⁿ + p₁(x)Dⁿ⁻¹ + · · · + p_n(x). So the DE is L[y(x)] = g(x).

Linearity Property

L[c₁y₁(x) + c₂y₂(x)] = c₁L[y₁(x)] + c₂L[y₂(x)]

Fundamental Set

For homogenous linear DE of order n, there are a set of linearly independent solutions. The general solution of the homogeneous DE L[y] = 0 is y_h = c₁y₁ + · · · + c_ny_n for any constants c_j

Particular Solution

L[y]=g, gen sol is y=y_p+y_h

Constant Coefficient Linear DE

L[y] = 0 with L = Dⁿ + p₁Dⁿ⁻¹ + · · · + p_n
for constants p_j

Auxiliary Equation

rⁿ + p₁rⁿ⁻¹ + · · · + p_n = 0

Real root with multiplicity of k

e^rx(c₁ + c₂x + · · · + c_kx^k−1)

Complex root with multiplicity of k

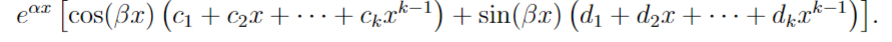
Higher-Order Cauchy Euler DE

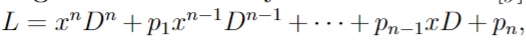
Auxiliary Equation for Cauchy-Euler (try y=x^r)

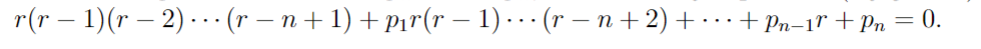
Real Roots Sol for Cauchy-Euler

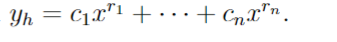
Real root sol with multiplicity of k for Cauchy-Euler

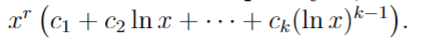
Complex root sol with multiplicity of k for Cauchy-Euler

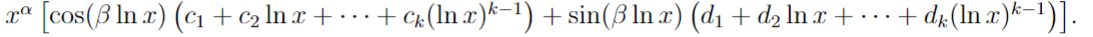
Annihilator

Set of all functions for a homogeneous solution

Annihilator Method

factor L into powers of (D-r)^k and [(D-a)²+B²]^k. Add corresponding annihilators to get y_h

Laplace Transformation

Converges for s>a,

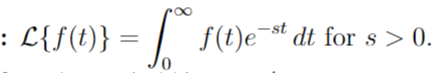
Derivative Property

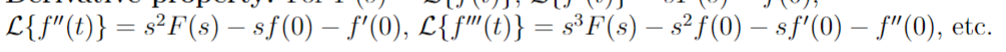
Laplace Transformation Method

When to use partial fraction decomposition

During the laplace transformation method

Partial Fractions Decomposition

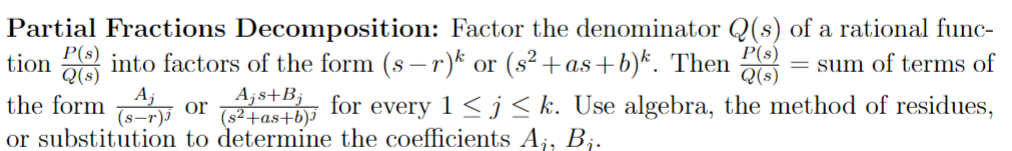
When to use Heaviside Step Functions

When handling continuous piecewise functions

Periodic Functions

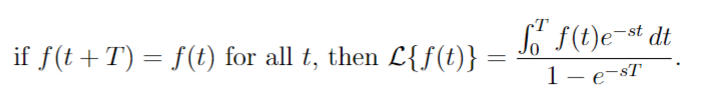
Convolution Theorem

No product rule used!!!

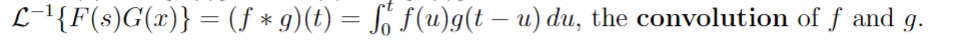
Dirac Delta Function

S(t-a)

Property of a dirac delta function in a impulse function

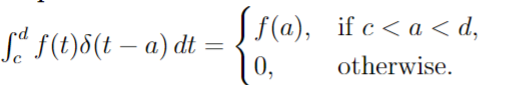
Impulse Function Purpose

model impulse force delivered at t=a

Impulse Function Laplace Transformation