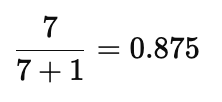GB307 Generalized Linear Model

What does standard linear regression assume?

• the relationship between X’s and Y is linear

• the errors are normally distributed

Standard Linear Regression Equation

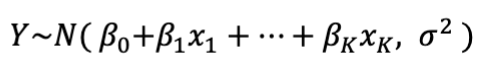
What are Generalized Linear Models (GLMs)?

an extension of linear regression that allow for non-normal response variable distributions and a flexible link between predictors and the mean of the outcome

What are the two key features that make GLMs different from linear regression?

• The response variable Y can have a non-normal distribution.

• The mean of Y, E(Y|X), is linked to a linear combination of predictors through a function.

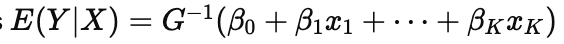
What does this equation mean in GLMs?

the mean function

What is the link function in a GLM?

G (⋅) connects the expected value of Y to the linear combination of predictors

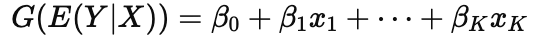
Why use GLMs instead of linear regression?

Because linear regression assumes normal errors and a constant variance. GLMs allow for different distributions (like binomial or Poisson) and more flexible relationships.

What is the identity link function in GLMs used for?

• Used for linear relationships.

• Link: β₀ + β₁x₁ = E(Y|X)

• Mean: E(Y∣X) = β₀ + β₁x₁

When should you use the log link function in a GLM?

• When the mean must be positive, like with count data.

• Link: β₀ + β₁x₁ = ln(E(Y|X))

• Mean: E(Y∣X) = e^{β₀ + β₁x₁}

What kind of relationships does the power link handle in GLMs?

• Used for curved (non-linear) relationships.

• Link: β₀ + β₁x₁ = E(Y|X)^a

• Mean: E(Y|X) = (β₀ + β₁x₁)^1/a

How are the link and mean functions related in GLMs?

The link function transforms the mean so the model can be expressed as a linear combination of predictors. The mean function is the inverse of the link function.

When should you use the Normal distribution for P(Y|X)?

Use it when the outcome is bell-shaped, can be positive or negative, and you're modeling averages (e.g., sales, stock changes)

What kind of data is appropriate for the Gamma distribution?

Use it when the response is always positive and may be skewed, like wait times, durations, or time between events.

How is the Normal distribution shaped and what can it model?

The Normal distribution is symmetric and bell-shaped, and it can model values that are negative or positive. Great for modeling things like sales or returns

Why would you choose the Gamma distribution over Normal?

Gamma is used when the data is strictly positive and may be skewed (e.g., time, rates). Normal can’t model skew or enforce positive-only outcomes.

When should you use the Bernoulli distribution for P(Y|X)?

Use it when the outcome is binary (0 or 1), like yes/no or success/failure questions

What kind of data does the Bernoulli distribution model?

Binary outcomes — data with only two possible values (0 or 1). Great for modeling the probability of an event happening.

When should you use the Poisson or Negative Binomial distribution?

Use them for count data:

• Poisson: assumes fixed variance

• Negative Binomial: handles extra variation (overdispersion)
  Examples:

• Number of customers per hour

• Number of defects per product

What types of data are modeled with Poisson or Negative Binomial?

Positive integers — like how many times something happens. These models are used when the outcome is a count.

Normal Distribution

bell shaped, continuous

Gamme Distribution

positive, continuous, skewed

Bernoulli Distribution

Binary

Poisson/Negative Binomial Distribution

positive integers

What is the goal when fitting a GLM?

To estimate the coefficients β^​, and use them to predict the expected value or characteristics of Y through

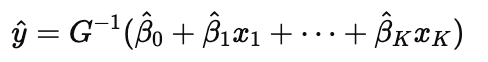
How do we estimate the coefficients β^ in a GLM?

We use maximum likelihood estimation — we choose the values of β^ that maximize the probability of observing our data given the model.

What does maximizing the likelihood mean in GLMs?

It means finding β^​ that gives the highest joint probability of all observed Y_i values given their predictors X_i:

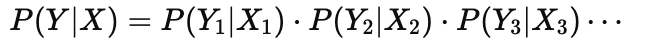
What is the average likelihood in a GLM?

• It is the geometric mean of the individual likelihoods:

• It represents the average probability of observing each outcome, mostly used in discrete cases

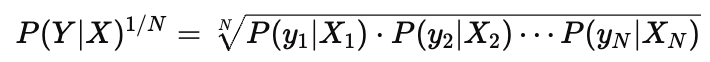
Why is the average log-likelihood often used in continuous cases?

Because the average likelihood can become very small, especially with many observations. Taking the log makes the value more interpretable and numerically stable.

What is the formula for the average log-likelihood?

It’s the mean of the log-probabilities

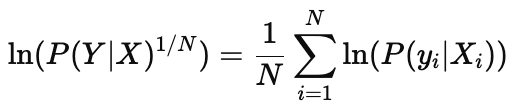
What does the log-likelihood measure in a model?

It measures how well the model explains the data. Higher values mean the model assigns higher probability to the observed outcomes.

What does the Average Likelihood Ratio (ALR) compare?

It compares how well two models (A and B) explain the data by taking the geometric average of the likelihoods from each model:

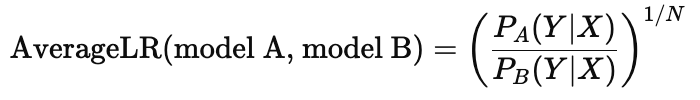
What does an Average Likelihood Ratio of 3 mean?

It means that, on average, each observation is 3 times more likely under model A than model B

Why use a geometric average for likelihood ratios?

Because individual likelihoods are multiplied together (not added), using the geometric mean gives a more balanced comparison across all observations

What is the Akaike Information Criterion (AIC) used for?

To compare models that may have different numbers of predictors. It adjusts for complexity so models with more variables don’t get an unfair advantage

What is the formula for AIC?

• K = number of parameters (predictors)

• P(Y∣X) = likelihood of the model

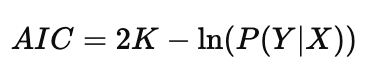
How should AIC be interpreted when comparing models?

Lower AIC is better. It means a better balance between fit and simplicity.

What does it mean if one model has an AIC 2 units lower than another?

That model is considered significantly better

What kind of distribution does a Logit Model use?

A Bernoulli distribution, because the outcome is binary (either 0 or 1). It models the probability that Y = 1 given X

What does the Logit Model predict?

It predicts the probability that the outcome is 1, using the inverse of the logit link function

What is the mean function of a Logit Model?

This ensures the predicted value (probability) is always between 0 and 1.

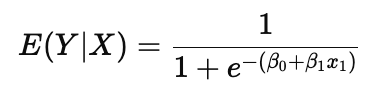
Why does the Logit model use a logistic curve?

Because it models probability smoothly between 0 and 1 and captures the S-shaped (sigmoid) relationship often seen in binary outcomes

What is the systematic component in a Logit Model?

• It’s the linear combination of the predictors: β₀+β₁x_1- +⋯

• This part models the log-odds of success

What is the log-odds formula in logistic regression?

This shows how the predictors influence the log of the odds of the outcome being 1

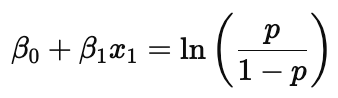
When is the predicted probability E(Y|X) = 0.5 in a logit model?

When the linear part (systematic component) equals zero: β₀+β₁x₁ = 0

What do odds of 7:1 mean?

It means there are 7 successes for every 1 failure — the probability of success is 0.875