12 Basic Functions w/ Graphs
1/11
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
12 Terms
The Identity Function
y=x
Domain: ALL REALS
Range: ALL REALS
Discontinuities: None
Decreasing Intervals: None
Increasing Intervals: (-∞,∞)
Symmetry: ODD (about the origin)
Bounded: Unbounded or NONE

The Squaring Function
y = x^2
Domain: ALL REALS
Range: [0,∞)
Discontinuities: None
Decreasing Intervals: (-∞,0]
Increasing Intervals: [0,∞)
Symmetry: EVEN (across y-axis)
Bounded: Bounded Below
![<p>Domain: ALL REALS</p><p>Range: [0,∞)</p><p>Discontinuities: None</p><p>Decreasing Intervals: (-∞,0]</p><p>Increasing Intervals: [0,∞)</p><p>Symmetry: EVEN (across y-axis)</p><p>Bounded: Bounded Below</p>](https://knowt-user-attachments.s3.amazonaws.com/632beef0-3e95-4f26-9dbd-229381ddb6a7.jpg)
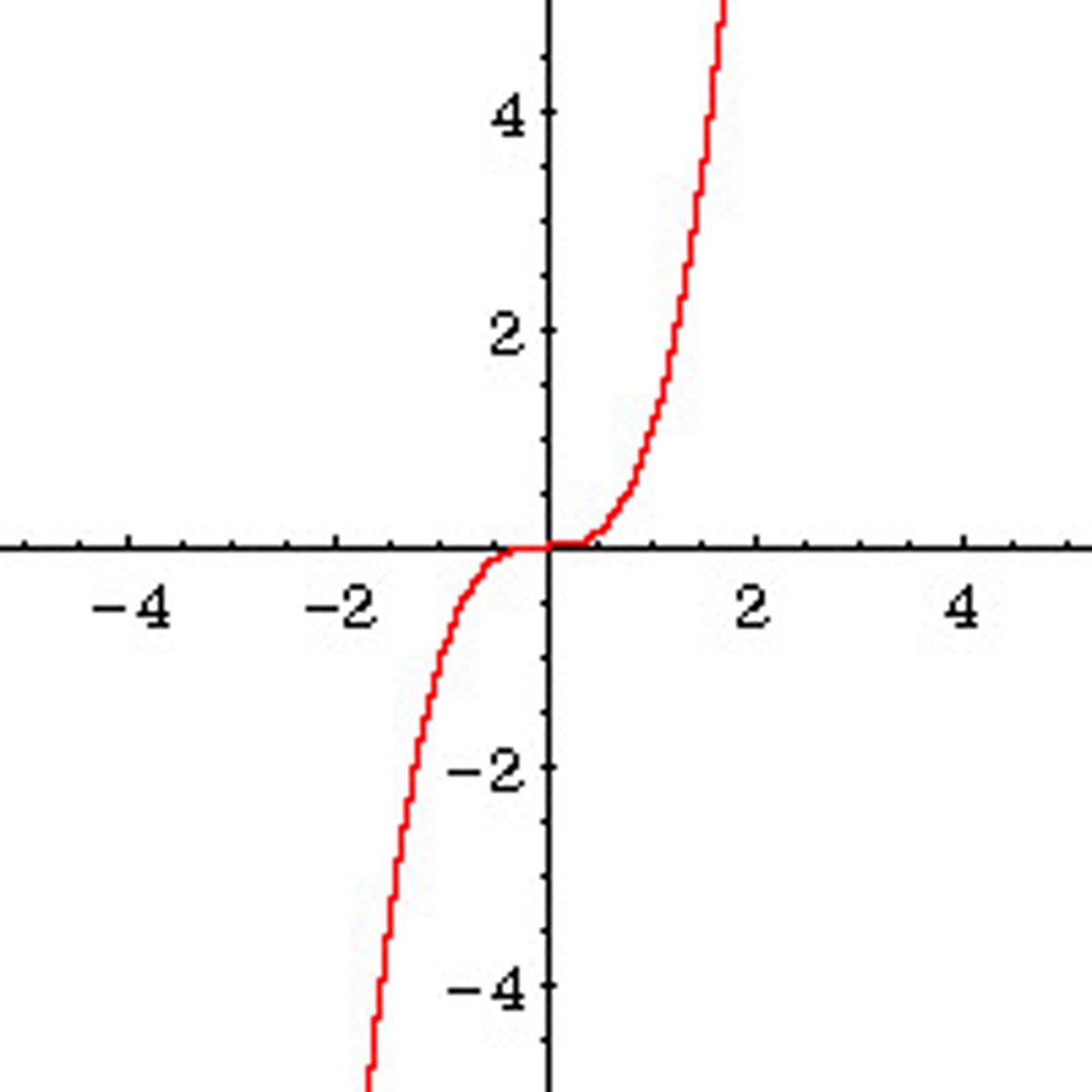
The Cubing Function
y=x^3
Domain: ALL REALS
Range: ALL REALS
Discontinuities: NONE
Decreasing Intervals: NONE
Increasing Intervals: All REALS
Symmetry: ODD (about the origin)
Bounded: Unbounded or NONE
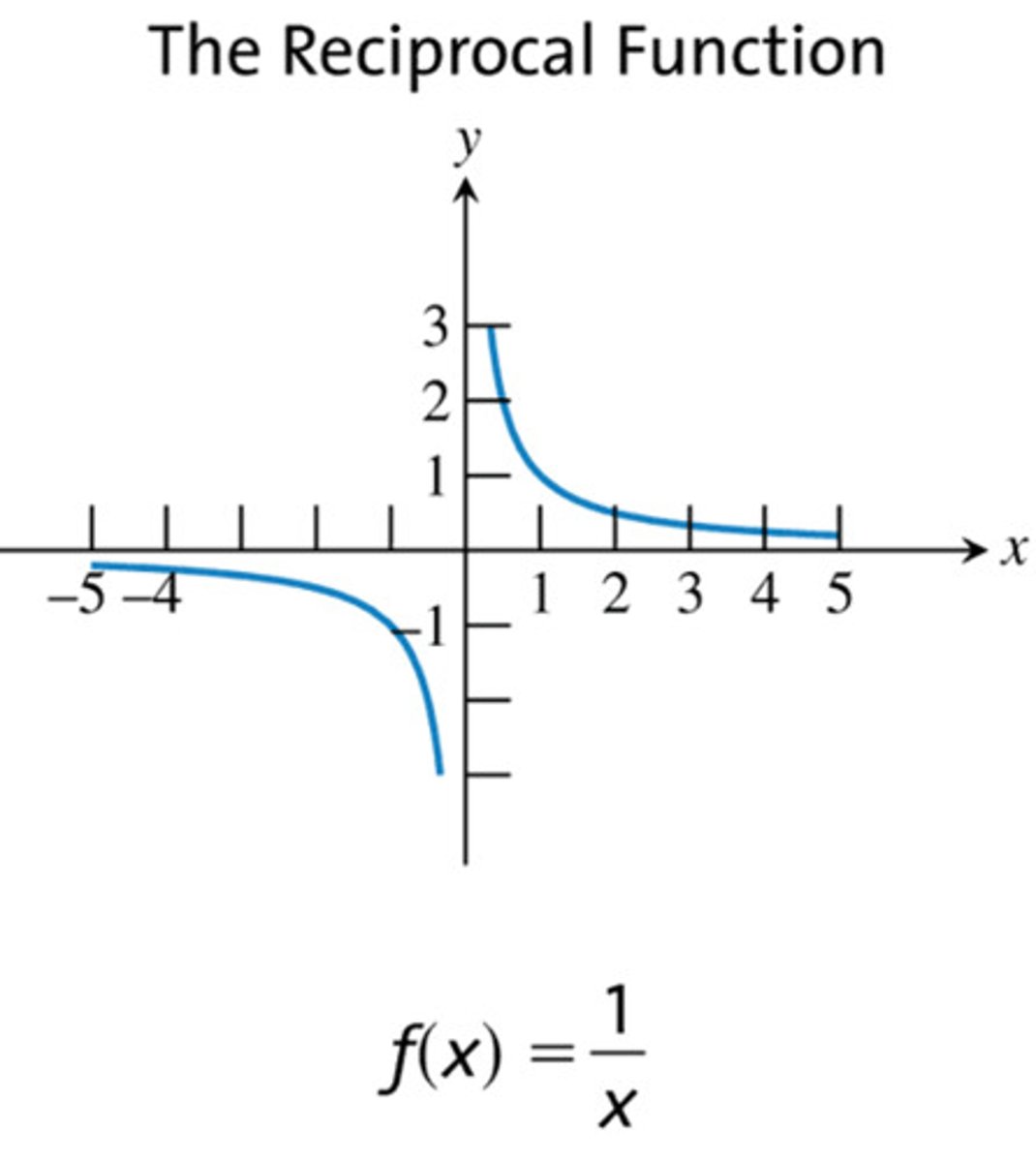
The Reciprocal Function
y=1/x
Domain: (-∞,0) ∪ (0,∞)
Range: (-∞,0) ∪ (0,∞)
Discontinuities: NONE **Asymp @ x=0 (VA)**
Decreasing Intervals: (-∞,0)
Increasing Intervals: (0, ∞)
Symmetry: ODD (about the origin)
Bounded: Not Bounded or NONE
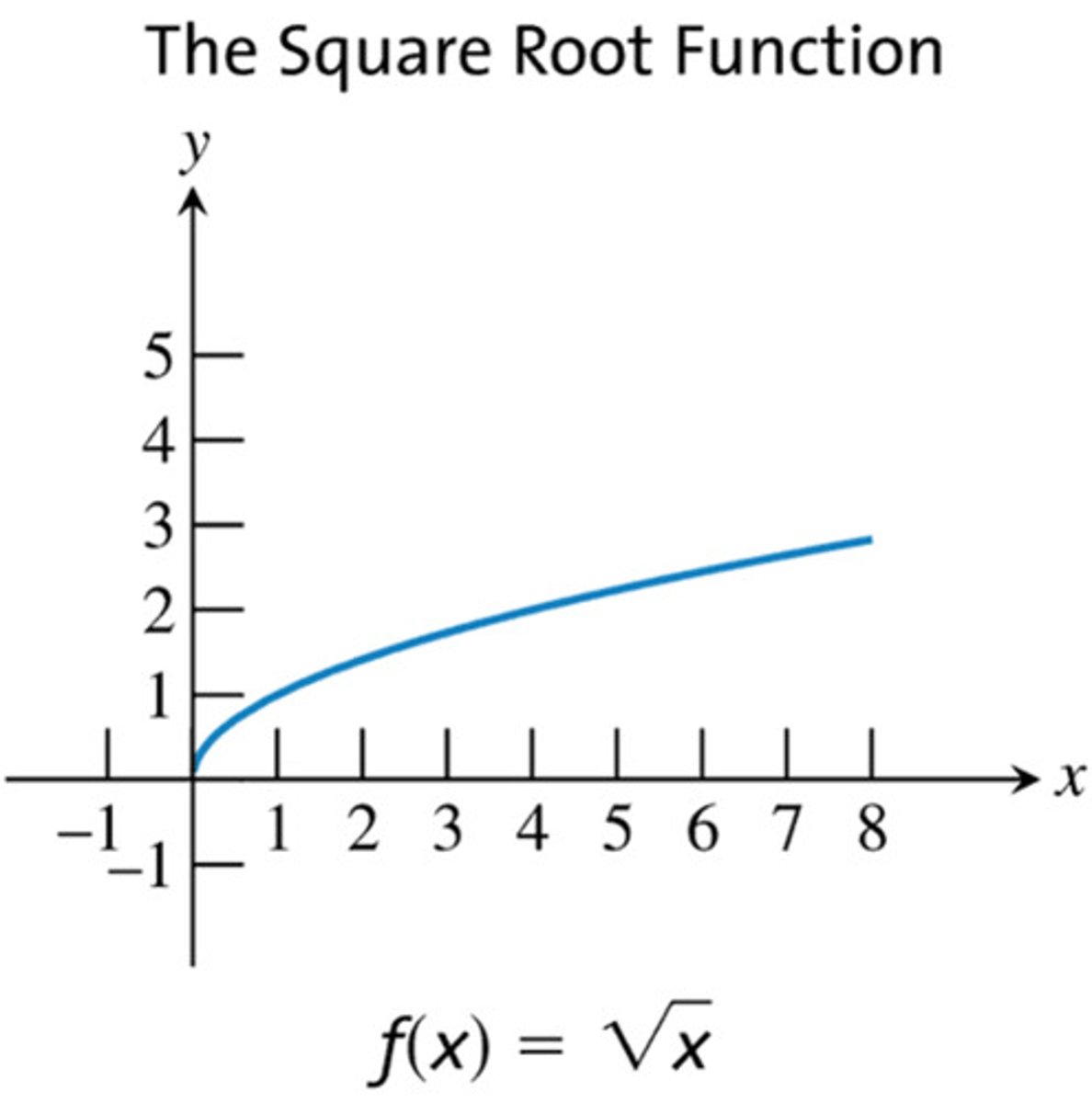
The Square Root Function
y=√x
Domain: [0,∞)
Range: [0,∞)
Discontinuities: NONE
Decreasing Intervals: NONE
Increasing Intervals: [0, ∞)
Symmetry: NONE
Bounded: Bounded Below
The Absolute Value Function
y=|x|
Domain: ALL REALS
Range: [0,∞)
Discontinuities: NONE
Decreasing Intervals: (-∞, 0]
Increasing Intervals: [0, ∞)
Symmetry: EVEN (across the y-axis)
Bounded: Bounded Below
![<p>Domain: ALL REALS</p><p>Range: [0,∞)</p><p>Discontinuities: NONE</p><p>Decreasing Intervals: (-∞, 0]</p><p>Increasing Intervals: [0, ∞)</p><p>Symmetry: EVEN (across the y-axis)</p><p>Bounded: Bounded Below</p>](https://knowt-user-attachments.s3.amazonaws.com/65ed071d-3948-4589-a1b9-fe34afee70a1.jpg)
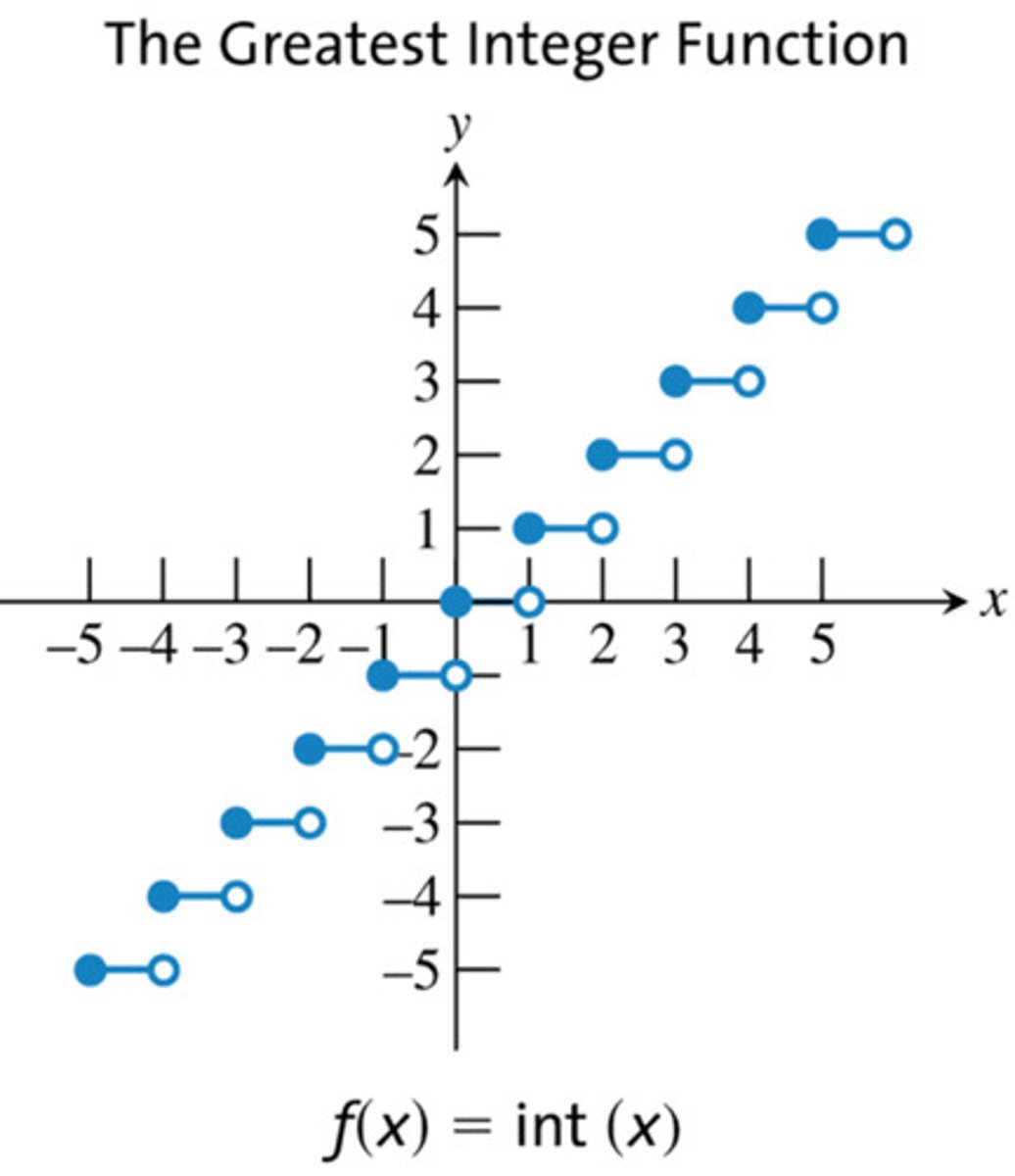
The Greatest Integer Function
y=int(x)
Domain: ALL REALS
Range: Integers or "Z"
Discontinuities: Multiple Jumps
Decreasing Intervals: NONE
Increasing Intervals: By Integers
Symmetry: NONE
Bounded: Unbounded or NONE
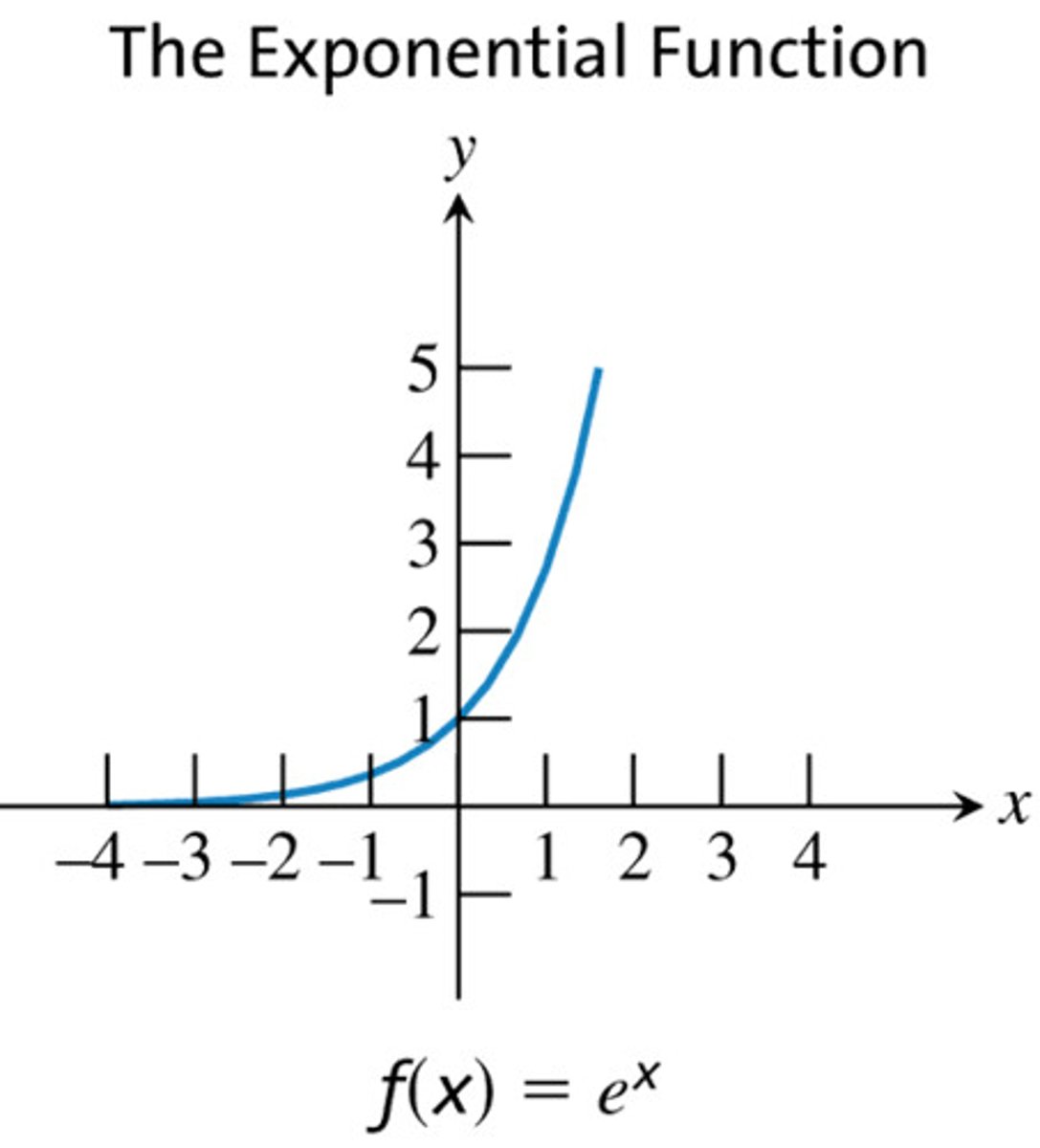
The Exponential Function
y=e^x
Domain: ALL REALS
Range: (0,∞)
Discontinuities: NONE
Decreasing Intervals: NONE
Increasing Intervals: (-∞,∞)
Symmetry: NONE
Bounded: Bounded Below
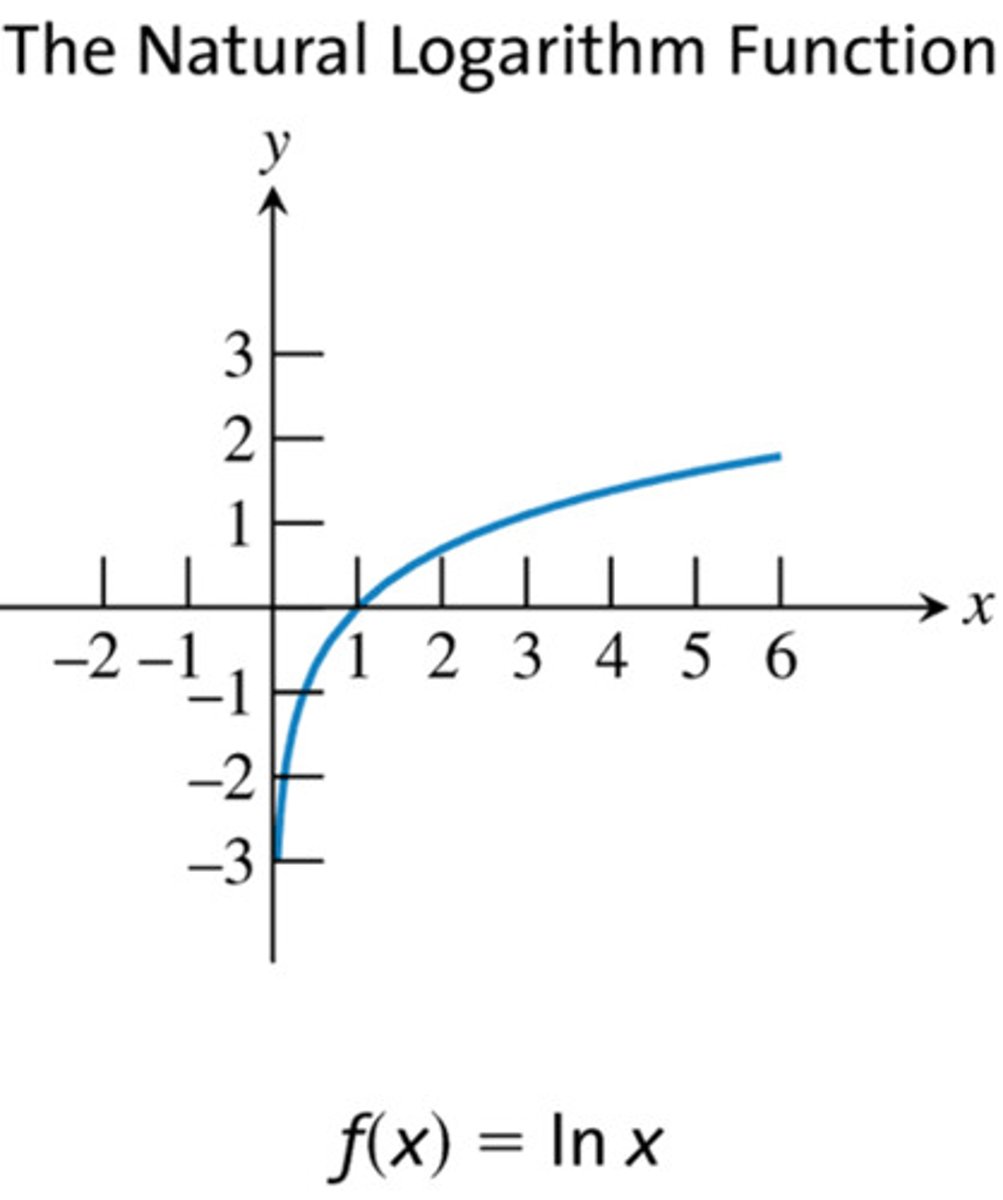
The Natural Log Function
y=ln(x)
Domain: (0,∞)
Range: ALL REALS
Discontinuities: NONE **Asymp @ x=0 (VA)**
Decreasing Intervals: NONE
Increasing Intervals: (-∞,∞)
Symmetry: NONE
Bounded: Unbounded or NONE
The Sine Function
y=sin(x)
Domain: ALL REALS
Range: [-1,1]
Discontinuities: NONE
Decreasing Intervals: It Alternates
Increasing Intervals: It Alternates
Symmetry: ODD (about the origin)
Bounded: Bounded or BOTH @ y=1 & y=-1
![<p>Domain: ALL REALS</p><p>Range: [-1,1]</p><p>Discontinuities: NONE</p><p>Decreasing Intervals: It Alternates</p><p>Increasing Intervals: It Alternates</p><p>Symmetry: ODD (about the origin)</p><p>Bounded: Bounded or BOTH @ y=1 & y=-1</p>](https://knowt-user-attachments.s3.amazonaws.com/50ef5bd8-611b-4fb7-ba1f-99c71f6b9a93.jpg)
The Cosine Function
y=cos(x)
Domain: ALL REALS
Range: [-1,1]
Discontinuities: NONE
Decreasing Intervals: It Alternates
Increasing Intervals: It Alternates
Symmetry: EVEN (across the y-axis)
Bounded: Bounded or BOTH @ y=1 & y=-1
![<p>Domain: ALL REALS</p><p>Range: [-1,1]</p><p>Discontinuities: NONE</p><p>Decreasing Intervals: It Alternates</p><p>Increasing Intervals: It Alternates</p><p>Symmetry: EVEN (across the y-axis)</p><p>Bounded: Bounded or BOTH @ y=1 & y=-1</p>](https://knowt-user-attachments.s3.amazonaws.com/140eaa16-f429-4f49-a88a-c755f1d05460.jpg)
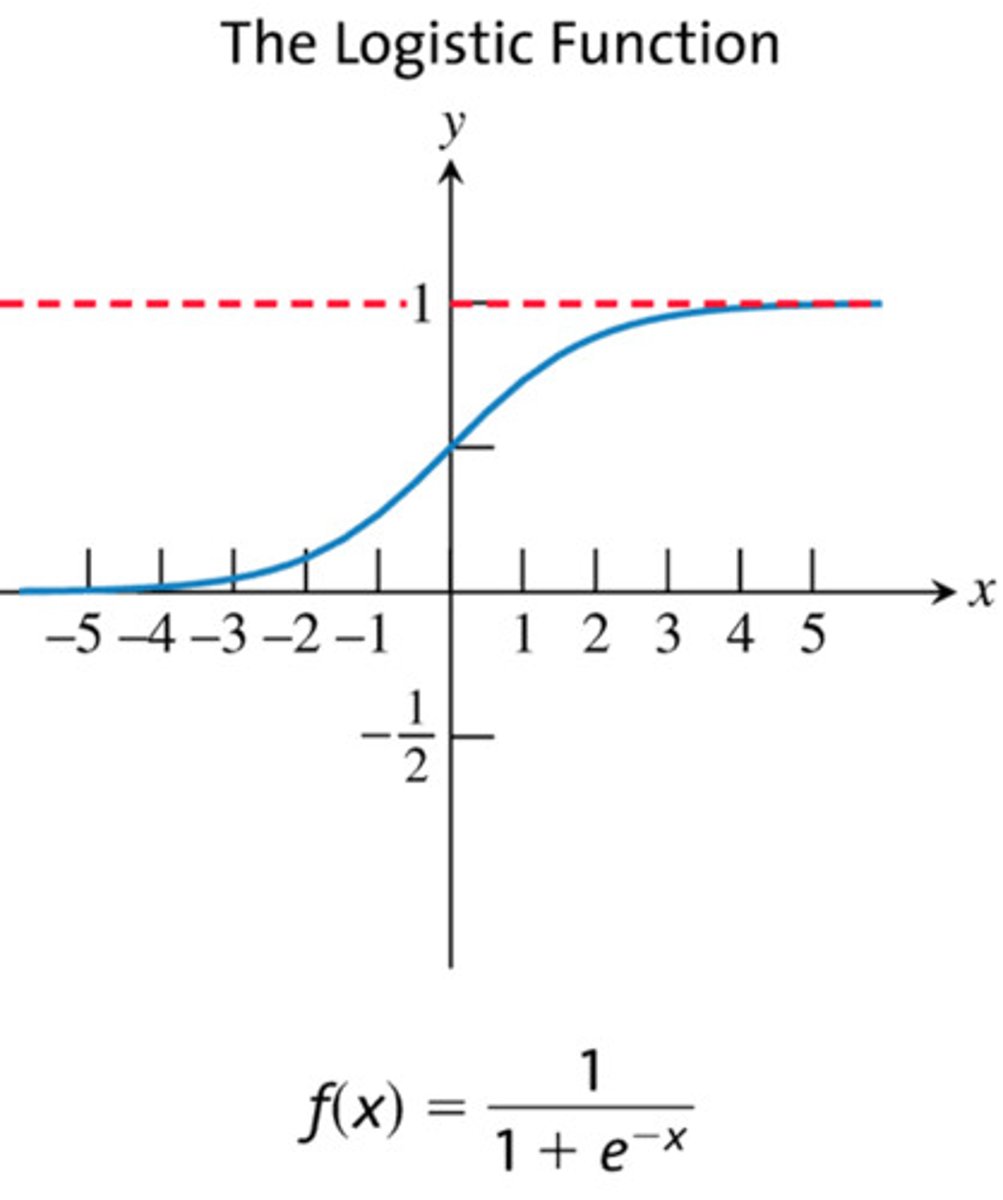
The Logistic Function
y=1/1+e^-x
feel free to change scale of graph
Domain: ALL REALS
Range: (0,1)
Discontinuities: NONE **Asymp @ y=0 & y=1 (HA)**
Decreasing Intervals: NONE
Increasing Intervals: ALL REALS
Symmetry: NONE
Bounded: Bounded or BOTH @ y=0 & y=1