MATH1151 Algebra

Co-Efficient Matrix

Ax=b

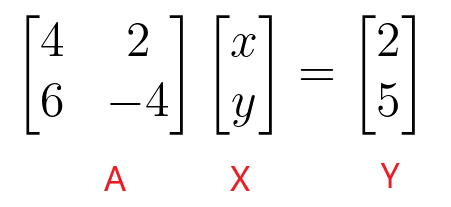
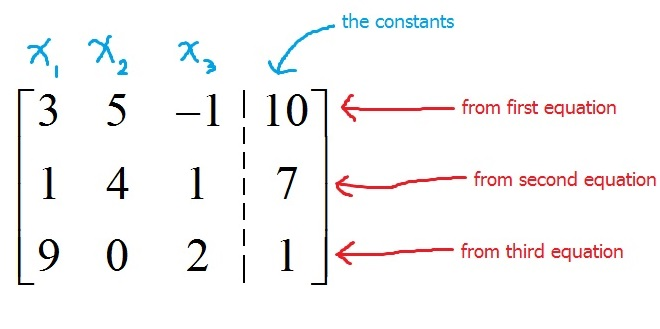
Augmented Matrix

(U | Y)

Linear Combination

Span of two non parallel vectors will make a plane

Span of two parallel vectors is line through the origin

Plane Definition for n dimensions

X=a+bu+cv

Hyperplanes in n dimensions

X=a+bu₁+cu₂+…+nu_n-1

Leading Row

A row which isn’t all zeroes

Leading entry/element

Left most non zero term

Leading Column

Column containing the leading entry. There can be multiple leading columns.

No solution

When the right hand column, is the leading column, ie

(0 0 0 | 2)

Unique solution

When every variable (x₁, x₂, … x_n) is a leading variable

Infinite solution

When there are more variables than leading rows

Row Echelon Form (REF)

• All zero rows must be at the bottom

• All leading entries must be to the right of the above

Reduced Row Echelon Form (RREF)

• All leading entries/elements must be 1

• All above leading entries must be 0

Leontief Analysis

Output of each industry is distributed among various sectors, sectors are dependent on each other

Transpose

Swap rows and columns

Symmetric Matrix

Transpose is equal to original

Tranpose Determinant

Transpose of determinant is equal to determinant

Determinant Zero

• Has zero row/column

• Any column/row is a multiple of another

Scaler Multiplication Property of Determinants

If k rows or columns are multiplied by a scaler, then det(A) will be multiplied by a^k

Determinant Unchanged

Adding a multiple of one row to another

Multiplicative Property of Determinants

If both A and B square matrices, then:

det(AB)=det(A)det(B)

Note this result is commutative

Determinant of a Triangular Matrix

If U is a matrix in row echelon form, then det(U) can be found by multiplying all the values along the diagonal