Ch 6 - Inequalities & Absolute Values
1/40
Earn XP
Description and Tags
Must Know Concepts
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
41 Terms
When have to divide or multiply an inequality by a negative number, you…
you must reverse the sign
When do you reverse the inequality sign?
When you divide or multiply by a negative number
How do you add inequalities together?
You need to check the direction the signs are facing. If they’re facing the same direction, you can add them
When can you add inequalities together?
When the signs are facing the same direction
How do you solve problems with an equation and inequality?
Solve for a variable and plug the equation into an inequality
When dealing with a compound inequality you must…
make sure to do the operations to both sides of the inequality
You can only multiply or divide an inequality by a variable when…
you know the sign of the variable. you need to know if you need to reverse the inequality sign or not
What method can you use to compare the size of multiple inequalities?
Make a number number line
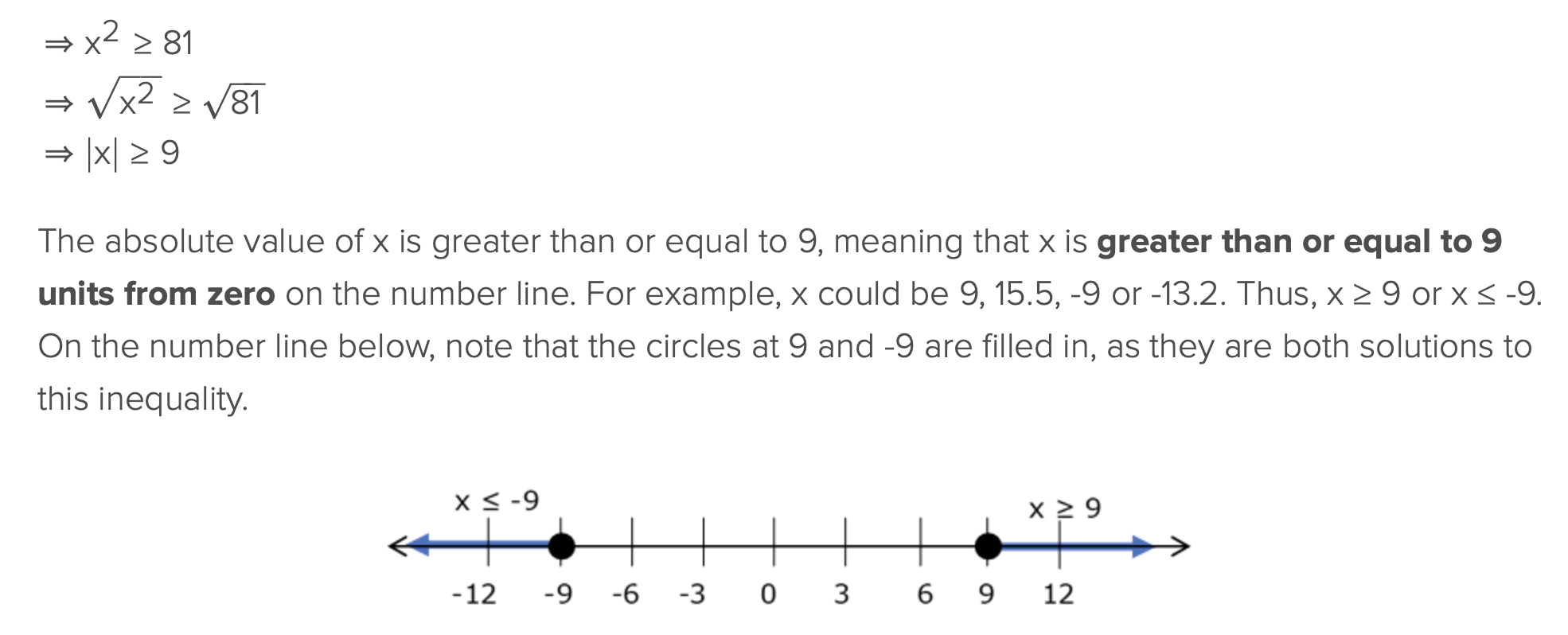
If x2 + 10 > 110, then which of the following could be the value of x?
8, -10, -12 (can select multiple answers)
-12
If x2 > b and b is positive then, the√x is…
x is greater than the square root of b
x less than the negative of the square root of b
x > √b and x < √b
If x2 < b and b is positive then, the√x is…
x is less than the square root of b
x less than the negative of the square root of b
If 2 absolute value of 2 expressions are equal, it must be true that….
the expressions in the absolute values bars are either equal or opposite
the absolute value of the sum of 2 numbers, a and b, will always be _________ the absolute value of the 2 individual numbers?
| a + b | ??? |a| + |b|
less than or equal to
| a + b | ≤ |a| + |b|
If a and b are 2 non-zero numbers, and | a + b |= |a| + |b|, then |a| + |b|…
must have the same sign
|a - b| ??? |a| - |b|
|a - b| ≥ |a| - |b|
the absolute value of the subtraction of 2 numbers, a and b, will always be greater than the absolute value of the 2 individual numbers
If b ≠ 0 and |a-b| = |a| - |b|, then a and b must…
a and b must….
have the same sign
|a| ≥ |b|
if |x| < b, we know that…
x < b and x > -b
b < x < -b (other way to format it)
x would be between the 2 values on a number line

if |x| > b, we know that…
x > b
x < -b
When are there no solutions to an absolute value problem?
When the absolute value of an expression is equal to a negative number
When do you need to check an absolute value equation for extraneous solutions?
When there’s a variable on both sides of the absolute value equation
if |x| = |y|, what do we know about x?
either x = y or x = -y
We shouldn’t multiply or divide by a variable in inequality problem unless…
we know the sign of the variable (so that we know if we need to flip the inequality)
How are |a - b| and |a| - |b| ordered?
|a - b| ≥ |a| - |b|
|a - b| will always be greater than
If |a - b| = |a| - |b|, this means…
the second quantity is 0
both qualities (a and b) have the same sign
How are |a + b| and |a| + |b| ordered?
|a + b| ≤ |a| + |b|
|a + b| is less than
If |2x + 4| = 12, what are 2 possible values of x?
If 2x + 4 = 2x + 4, then 2x + 4 = 12 → 2x = 8 → x = 4
If 2x + 4 = -(2x + 4), then -2x - 4 = 12 → -2x = 16 → x = -8
4 and -8
if x² = |x|, then x must be…
1, 0, or -1
if x is not one of the 3 values then x² > |x| or x² < |x|
if x² < |x|, then x must be…
x must be between 0 and -1
-1 < x < 0
bc if x² = |x|, x can only be 0,1, or -1
if x² > |x|, then x must be…
x < -1 or x > 1
Solve | x + 1 | = -1
you can’t. an absolute value is equal to a negative number which isn’t possible
What happens when an inequality is multiplied or divide by a negative number?
The inequality sign must be reversed
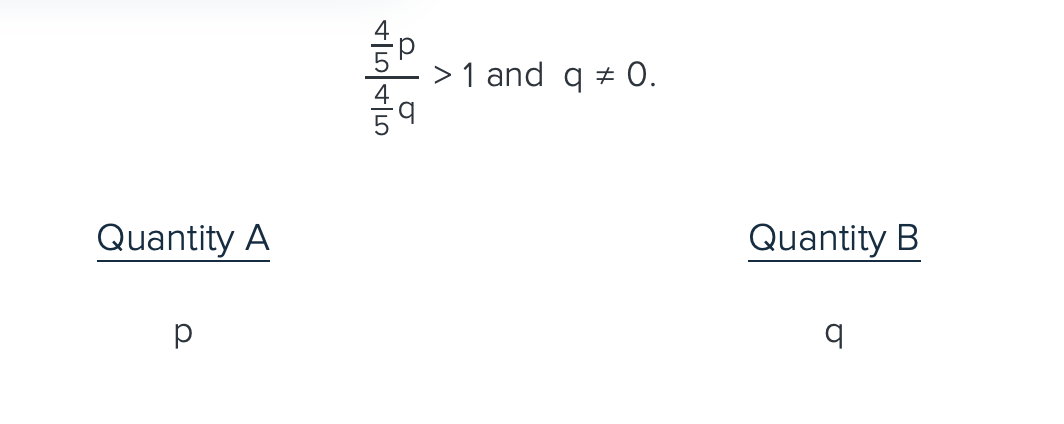


Reminder: 0 is a multiple of very number

If 2 absolute values are equal, what do you know about the expression within the absolute value bars?
the expressions within the absolute value bars are either:
equals
|5| = |5| or |-5| = |-5|
have opposite signs
|5| = |-5| or |-5| = |5|


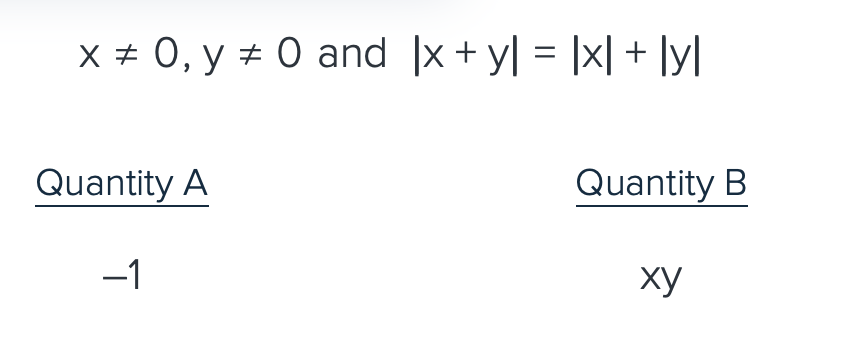
QB is greater bc xy and must have the same sign


if |a - b| = |a| - |b| and b ≠ 0, then what do you know?
a and b must have the same sign & |a| ≥ |b|
If the absolute value of an expression is a negative number,
there will be no solutions to that equation
|x + 1| = -2
there’s is no solutions. an absolute value cannot be equal to a negative number


