Psychological Statistics Exam 4

Multivariate Analysis Consists of…

-Two or more dependent variables

-No categories

General Purpose of Multivariate Analysis

-To test for relationships between two or more values

-When this number increases, what does that number do?

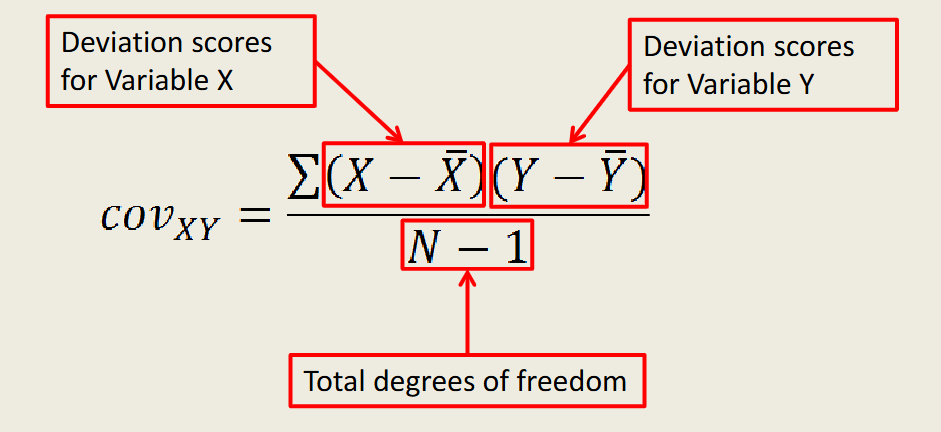
Covariance

The amount of variance shared between two variables

-Each deviation score on Variable X is paired with and multiplied by a deviation score on Variable Y from the same participant

-Positive scores on X & negative scores on Y (or vice versa) will yield a negative number

-Positive or negative scores on both X and Y will yield a positive number

Two different types of Multivariate Test:

1) Correlation

2) Regression

Correlation

comparison of two values to each other

-As values on one variable increase, what do values on the other variable do?

Regression

-comparison between 1 (or more) predictor and 1 outcome variables

-Results framed in terms of cause and effect

-The predictor(s) causes the outcome

-Stronger test than correlation, which tells us nothing about cause

positively correlated

-when a correlation has a positive sign

-the two variables have a positive relationship. Scores on two variables that are_____,trend together in the same direction.

ex: Shoe size and height are likely to be positively correlated because taller than average people are likely to wear larger than average shoes and vice versa

negatively correlated

-when a coefficient has a negative sign

-negative/inverse relationship. Scores on two variables that are ____, trend in opposite directions from each other

ex: stress and happiness

uncorrelated

-a correlation of zero indicates a relationship that is neither positively nor negatively correlated

-there is no predictable relationship between scores on one variable and scores on the other

-social scientists will often refer to variables as ____ if the coefficient is very close to zero without being precisely zero

Relationship of DVs can be described in two factors:

1) Strength

2) Direction

Strength

the amount of variance shared by a given pair of variables

Correlation Coefficient

-Relationship described by one value

-Absolute values range from 0.00 to 1.00

-Measures the amount of variance shared by two variables

-0.00=no relationship

-1.00=perfectly related

Third Variable Problem

an unseen variable influences both the independent and dependent variables in a study. This can lead to a false correlation between the observed variables. For example, an apparent link between ice cream sales and drowning incidents could be attributed to a third variable, such as the warmer weather, which causes both to increase.

Pearson’s r

-test statistic for covariance

-the value you get for covariance is going to be affected by the size of the related standard deviations and the original scale values

-not easily interpreted as an absolute value, so we standardize it into r

-divide covariance by the deviations to control for standard deviation size

Heterogeneous Samples

are samples that consist of individuals with varied characteristics, which can lead to a broader representation of the population and varied results in statistical analyses.

Scatterplots

-special kind of graph that is used to display the relationship between two continuous variables

-each participant or case shows up as a dot in the graph

-displays scores on 2 variables simultaneously: 1 on the X axis and 1 on the Y axis

-the dot is located at the intersection between the score on the X axis and the score on the Y axis

Positive Correlation on a Scatterplot

coefficients trend upward as you move from left to right on the x axis

Negative Correlation on a Scatterplot

coefficients trend downward as you move from left to right on the X axis

Uncorrelated on a Scatterplot

coefficients neither trend upward nor downward

regression line

a mathematically derived straight line in a scatterplot that represents the idealized linear relationship between the two variables

B

-test statistic used for regression

-raw regression weight

-the amount of outcome variability accounted for by a predictor variable

-values vary as a function of the scale used

β (beta)

-test statistic for regression

-standardized regression weight

-Unlike B, does not vary as a function of the scale (like a z-score or correlation coefficient)

Unlike Correlation, Regression accounts for specific rate of change

-the bigger the slope, the higher the rate of change

-the higher the rate of change, the better a predictor that variable is for outcome variable

-one variable may be a stronger predictor

rho (ρ)

population correlation is abbreviated with___

Correlation Matrix

contains all the correlations among your chosen study variables. It is typically triangle-shaped, with each variable listed down the left side and also across the columns at the top. This arrangement allows room for each possible correlation between any two variables you have included. We identify a correlation by finding the table cell where the two variables meet