AP Stats Chapter 5: Key Probability Terms & Definitions

The probability that you will be ticketed for illegal parking on campus is about 1/3. During the last nine days, you have illegally parked every day and have NOT been ticketed (you lucky person!). Today, on the 10th day, you again decide to park illegally. Assuming the outcomes are independent from day to day, the probability that you will be caught is

a) 1/3

b) 1/3 + 1/3

c )1/3 -1/3

d) 1/10

e) 9/10

A

Car Bus Walk Total

Jr 146 106 48 300

Sr 146 64 40 250

Total 292 170 88 550

You select one student from this group at random. What is the probability that this student typically

takes a bus to school?

a. 0.256

b. 0.309

c. 0.353

d. 0.455

e. 0.604

B

170/550

Car Bus Walk Total

Jr 146 106 48 300

Sr 146 64 40 250

Total 292 170 88 550

You select one student from this group at random. If the student says he is a junior, what is the probability that he walks to school?

a. 0.073

b. 0.160

c. 0.455

d. 0.600

e. 0.833

B

48/300

Car Bus Walk Total

Jr 146 106 48 300

Sr 146 64 40 250

Total 292 170 88 550You select one student from this group at random. Which of the following statements is true about

the events "Typically walks to school" and "Junior?"

a. The events are mutually exclusive and independent.

b. The events are not mutually exclusive, but they are independent.

c. The events are mutually exclusive, but they are not independent.

d. The events are not mutually exclusive, nor are they independent.

B

Event A occurs with probability 0.2. Event B occurs with probability 0.8. If A and B are disjoint

(mutually exclusive), then

a. P(A or B) = 1.0.

b. P(A and B) = 0.16.

c. P(A and B) = 1.0.

d. P(A or B) = 0.16.

e. both A. and B. are true.

A

The probability of any outcome of a random phenomenon is

a. the precise degree of randomness present in the phenomenon.

b. any number as long as it is greater than 0 and less than 1.

c. either 0 or 1, depending on whether or not the phenomenon can actually occur or not.

d. the proportion of times the outcome occurs in a very long series of repetitions.

e. none of the above.

D

People with type O-negative blood are universal donors. That is, any patient can receive a transfusion of O-negative blood. Only 7.2% of the American population has O-negative blood. If 10 people appear at random to give blood, what is the probability that at least 1 of them is a universal

donor?

a. 0

b. 0.280

c. 0.526

d. 0.720

e. 1

C

(1-0.072)^10=0.473

1-0.473

You play tennis regularly with a friend, and from past experience, you believe that the outcome of each match is independent. For any given match you have a probability of 0.6 of winning. The probability that you win the next two matches is

a. 0.16.

b. 0.36.

c. 0.4.

d. 0.6.

e. 1.2.

B

0.6 x 0.6

There are 10 red marbles and 8 green marbles in a jar. If you take three marbles from the jar

(without replacement), the probability that they are all red is:

a. 0.069

b. 0.088

c. 0.147

d. 0.444

e. 0.171

c

(10/18)x(9/17)x(8/16)

Jun and Deron are applying for summer jobs at a local restaurant. After interviewing them, the restaurant owner says, "The probability that I hire Jun is 0.7, and the probability that I hire Deron is 0.4. The probability that I hire at least one of you is 0.9." What is the probability that both Jun and

Deron get hired?

a. 0.1

b. 0.2

c. 0.28

d. 0.3

e. 1.1

b

P(JUD)=P(J) + P(D) - P(JUD)

0.9 = 0.7 + 0.4 - P(JUD)

0..9=1.1-P(JUD)

A couple has two sons and decides to have a third child. The husband says, "We are bound to have a daughter this time; things balance out." The wife says, "Nonsense! Two boys in a row means we are more likely to have another boy." Comment on this disagreement based on your understanding of

probability.

The probability that a randomly selected person in the United States is left-handed is about 0.14.

(a) Use this probability to explain what the Law of Large Numbers says.

The probability that a randomly selected person in the United States is left-handed is about 0.14.

(b) Among the 28 students in Mr. Millar's Calculus BC class, 8 are left-handed. Could this have

happened by chance alone? Describe how you would use a random number table to simulate the

proportion of left-handers in a class of 28 students if they were chosen randomly from a population

that is 14% left-handed. Do not perform the simulation.

I would assign 0-13 as left handed and 14-99 as right handed. the select 2 diget numbers from a random number table. Then select 28 students and count the number of lefties. repeat a bunch of trails

The probability that a randomly selected person in the United States is left-handed is about 0.14.

(c) Below are the number of left-handers in 100 simulated classes of 28 students, assuming that

students are selected randomly from a population in which 14% of individuals are left-handed. What

do these results suggest about the proportion of lefties in Mr. Millar's class?

P(J) + P(F) - P(JUD)

In a statistics class there are 18 juniors and 10 seniors; 6 of the seniors are females, and 12 of the juniors are males. If a student is selected at random, find the probability of selecting

(a) a junior or a female

P(J) + P(F) - P(J and D)

(18/28)+(12/28)-(6/28)= 24/28=6/7=85.7%

In a statistics class there are 18 juniors and 10 seniors; 6 of the seniors are females, and 12 of the juniors are males. If a student is selected at random, find the probability of selecting

(b) not a junior male

1-P(J and D)

1- 12/28=16/28=4/7=57%

Suppose a person was having two surgeries performed at the same time by different operating teams.

Assume (unrealistically) that the two operations are independent. If the chances of success for surgery A are 85%, and the chances of success for surgery B are 90%, what is the probability that both will fail?

1-0.85=0.15

1-0.9=0.10

0.15 x 0.10=0.015=15%

Parking for students at Central High School is very limited, and those who arrive late have to park illegally and take their chances at getting a ticket. Joey has determined that the probability that he has to park illegally and that he gets a parking ticket is 0.07. He recorded data last year and found that because of his perpetual tardiness, the probability that he will have to park illegally is 0.25. Suppose that Joey arrived late once again this morning and had to park in a no-parking zone.

P(L and T)/ P(T)

0.07/0.25=0.28=28%

Consolidated Builders has bid on two large construction contracts. The company president believes that the probability of winning the first contract (event A) is 0.6, that the probability of winning a second (event B) is 0.3, and that the probability of winning both jobs is 0.1.

What is —the probability that Consolidated wins at least one of the job?

0.6+0.3-0.1=0.8 80%

Consolidated Builders has bid on two large construction contracts. The company president believes that the probability of winning the first contract (event A) is 0.6, that the probability of winning a second (event B) is 0.3, and that the probability of winning both jobs is 0.1.

Consolidated wins both jobs.

P(A and B)

0.1

Consolidated Builders has bid on two large construction contracts. The company president believes that the probability of winning the first contract (event A) is 0.6, that the probability of winning a second (event B) is 0.3, and that the probability of winning both jobs is 0.1.

Consolidated wins the first job but not the second.

P(A and B^c)= P(A)-P(A and B)

0.6-0.1=0.5

Consolidated Builders has bid on two large construction contracts. The company president believes that the probability of winning the first contract (event A) is 0.6, that the probability of winning a second (event B) is 0.3, and that the probability of winning both jobs is 0.1.

Either Consolidated does not win the first job or wins the second.

P(A^c and B)

0.4+ 0.3=0.7

Consolidated Builders has bid on two large construction contracts. The company president believes that the probability of winning the first contract (event A) is 0.6, that the probability of winning a second (event B) is 0.3, and that the probability of winning both jobs is 0.1.

Consolidated does not win either job.

P(A^c and B^c) = 1- P(A U B)

1-0.8=0.5

Event A occurs with a probability of 0.2. Event B occurs with a probability of 0.8. If A and B are disjoint (mutually exclusive) then

a) P(A or B) = 1.0

b) P(A and B)= 0.16

c) P(A and B)= 1.0

d) P(A or B)= 0.16

e) Both A and B are true

a

If PA. = 0.24 and PB. = 0.52 and A and B are independent, what is P(A or B)?

a) 0.1248

b) 0.28

c) 0.6352

d) 0.76

e) the answer can't be determined from the information given

C

P(A) + P(B) - P(A or B)

0.24 + 0.52 - (0.24-0.52)

In your top dresser drawer are 6 blue and 10 grey socks, unpaired and mixed up. One dark morning, you pull two socks from the drawer(without replacement, of course!). What is the probability that the two socks match?

a) 0.075

b) 0.375

c) 0.450

d) 0.500

e) 0.550

d

P(B and B) + P(G and G)

P(B and B) = P(B) x P(BIB)= (6-16)(5-15)=0.125

P(G and G) = P(G) x P(GIG)= (10/16)(9/15)=0.375

0.125+0.375

A recent survey asked 100 randomly selected adult Americans if they thought that women should be allowed to go into combat situations. Here are the results, classified by the gender of the subject

Yes No

M 32 18

F 16 34

The probability of a Yes answer, given that the person was a female, is

a) 0.16

b) 0.32

c) 1/3

d) 0.34

e) 0.42

b

16/50

A recent survey asked 100 randomly selected adult Americans if they thought that women should be allowed to go into combat situations. Here are the results, classified by the gender of the subject

Yes No

M 32 18

F 16 34

The probability that a randomly selected subject in the study is Male or Answer No is

a) 0.18

b) 0.68

c) 0.78

d) 0.84

e) 1.02

d

On the Centerville high school debate team, 20% of the members are sophomores, 35% are Jr, and 45% are Sr. A team member is selected randomly to give the closing argument. If sophomores, the team has a probability of 0.25 of winning the debate. If a Junior, the team has a probability of 0.6 of winning the debate. If a senior, the team has a probability of 0.85 of winning the debate.

Find the probability that the team wins the debate.

0.6425 (Find the probability that the selected student: Is a Sophomore AND Wins OR is a junior AND wins OR is a senior AND wins

On the Centerville high school debate team, 20% of the members are sophomores, 35% are Jr, and 45% are Sr. A team member is selected randomly to give the closing argument. If sophomores, the team has a probability of 0.25 of winning the debate. If a Junior, the team has a probability of 0.6 of winning the debate. If a senior, the team has a probability of 0.85 of winning the debate.

Given that the team lost the debate, what is the probability that it was a jr who gave the closing argument

P(LlJ)xP(J)/P(L)

P(L)= 1-P(W)

(0.4)(0.35)/P(0.3575)

=0.3916

The probability of any outcome of a random phenomenon is

a) the precise degree of randomness present in the phenomenon.

b) any number as long as it is greater than 0 and less than 1.

c) either 0 or 1, depending on whether or not the phenomenon can actually occur or

not.

d) the proportion of times the outcome occurs in a very long series of repetitions.

e) none of the above.

d. the proportion of times the outcome occurs in a very long series of repetitions.

Many fire stations handle emergency calls for medical assistance as well as those requesting firefighting equipment. A particular station says that the probability that an incoming call is for medical assistance is 0.81. This can be expressed as P(call is for medical assistance) = 0.81. Assume each call is independent of other calls.

(a) Describe what the Law of Large Numbers says in the context of this probability.

As the number of calls becomes larger and larger, the proportion of calls for medical assistance

will get closer and closer to 0.81.

Many fire stations handle emergency calls for medical assistance and those requesting firefighting equipment. The probability that an incoming call is for medical assistance is 0.81. This can be expressed as P(call is for medical assistance) = 0.81. Each call is independent of other calls.

You estimate the probability that exactly three of the next four calls are for medical assistance. Describe the design of a simulation. Explain clearly how you will use the table of random digits

Assign the digits 01 through 81 to calls for medical assistance and 82 through 00 to other calls. Choose four two-digit numbers from the random digits table and determine how many of the four calls are for medical assistance. Do this many times. The proportion of those trials that result in three calls for medical assistance is the

probability estimate.

or

U

and

upside down U

For mutually exclusive events

P(A or B) = P(A) + P(B)

For independent events

P(A and B) = P(A) x P(B)

General Addition Rule

P(A or B) = P(A) + P(B) - P(A and B)

General Multiplication Rule

P(A and B) = P(A) * P(B|A)

Conditional Probability

P(A|B) = P(A and B) / P(B)

A and B are independent if:

P(A)= P(AIB) or P(B)=P(BIA)

Two events A and B are mutually exclusive (disjoint)

if they have no outcomes in common and so can never occur together—that is, if P(A and B) = 0.

Two events A and B are independent if

the occurrence of one event does not change the probability that the other event will happen. In other words, events A and B are independent if P(A | B) = P(A) and P(B | A) = P(B).

Illegal music downloading has become a big problem: 29% of Internet users download music files, and 67% of downloaders say they don't care if the music is copyrighted.17 What percent of Internet users download music and don't care if it's copyrighted? Write the information given in terms of probabilities, and use the general multiplication rule.

P(AlB)=P(A and B) / P(B)

P(B)=P(DL and DC)

P(DL)=0.29

P(don't care l DL)= 0.69

(0.29)/(0.69)=0.19

According to Forrest Gump, "Life is like a box of chocolates. You never know what you're gonna get." Suppose a candy maker offers a special "Gump box" with 20 chocolate candies that look the same. In fact, 14 of the candies have soft centers and 6 have hard centers. Choose 2 of the candies from a Gump box at random.

Find the probability that one of the chocolates has a soft center and the other one doesn't.

(6/20)(14/20) + (14/20)(6/20) = .4421

Lactose intolerance causes difficulty in digesting dairy products that contain lactose (milk sugar). It is particularly common among people of African and Asian ancestry. In the United States (ignoring other groups and people who consider themselves to belong to more than one race), 82% of the population is white, 14% is black, and 4% is Asian. Moreover, 15% of whites, 70% of blacks, and 90% of Asians are lactose intolerant.19 Suppose we select a U.S. person at random.

(a) What is the probability that the person is lactose intolerant? Show your work.

P(W and L) + P(B and L) + P(A and L)

(0.15)(0.82) + (0.14)(0.7) + (0.04)(0.9) = 0.257

0.123 0.098 0.036

Lactose intolerance causes difficulty in digesting dairy products that contain lactose (milk sugar). It is particularly common among people of African and Asian ancestry. In the United States (ignoring other groups and people who consider themselves to belong to more than one race), 82% of the population is white, 14% is black, and 4% is Asian. Moreover, 15% of whites, 70% of blacks, and 90% of Asians are lactose intolerant.19 Suppose we select a U.S. person at random.

(b) Given that the person is lactose intolerant, find the probability that he or she is Asian. Show your work.

P(AlL)=P(A and L) / P(L)

0.036 / 0.257

You toss a pair of fair, six-sided dice in a board game. Tosses are independent. You land in a danger zone requiring you to roll doubles (both faces showing the same number of spots) before you can play again. How long will you wait to play again?

What is the probability of rolling doubles on a single toss of the dice? (If you need review, the possible outcomes appear in Figure 5.2 (page 306). All 36 outcomes are equally likely.)

(6/36)= 1/6

You toss a pair of fair, six-sided dice in a board game. Tosses are independent. You land in a danger zone requiring you to roll doubles (both faces showing the same number of spots) before you can play again. How long will you wait to play again?

What is the probability that you do not roll doubles on the first toss, but you do on the second toss?

(5/6)(5/6) + (1/6)(1/6)

You toss a pair of fair, six-sided dice in a board game. Tosses are independent. You land in a danger zone requiring you to roll doubles (both faces showing the same number of spots) before you can play again. How long will you wait to play again?

What is the probability that the first two tosses are not doubles and the third toss is doubles? This is the probability that the first doubles occurs on the third toss.

(5/6)(5/6)(1/6)

You toss a pair of fair, six-sided dice in a board game. Tosses are independent. You land in a danger zone requiring you to roll doubles (both faces showing the same number of spots) before you can play again. How long will you wait to play again?

Now you see the pattern. What is the probability that the first doubles occurs on the fourth toss? On the fifth toss? Give the general result: what is the probability that the first doubles occurs on the kth toss?

(5/6)^K-1 (1/6)

P(BlA)=

P(B and A) / P(A)

P(AlB)=

P(A and B) / P(B)

Sample Space (Probability)

when you list out every probability

probability model

lists the possible outcomes of a probability experiment and each outcome's probability

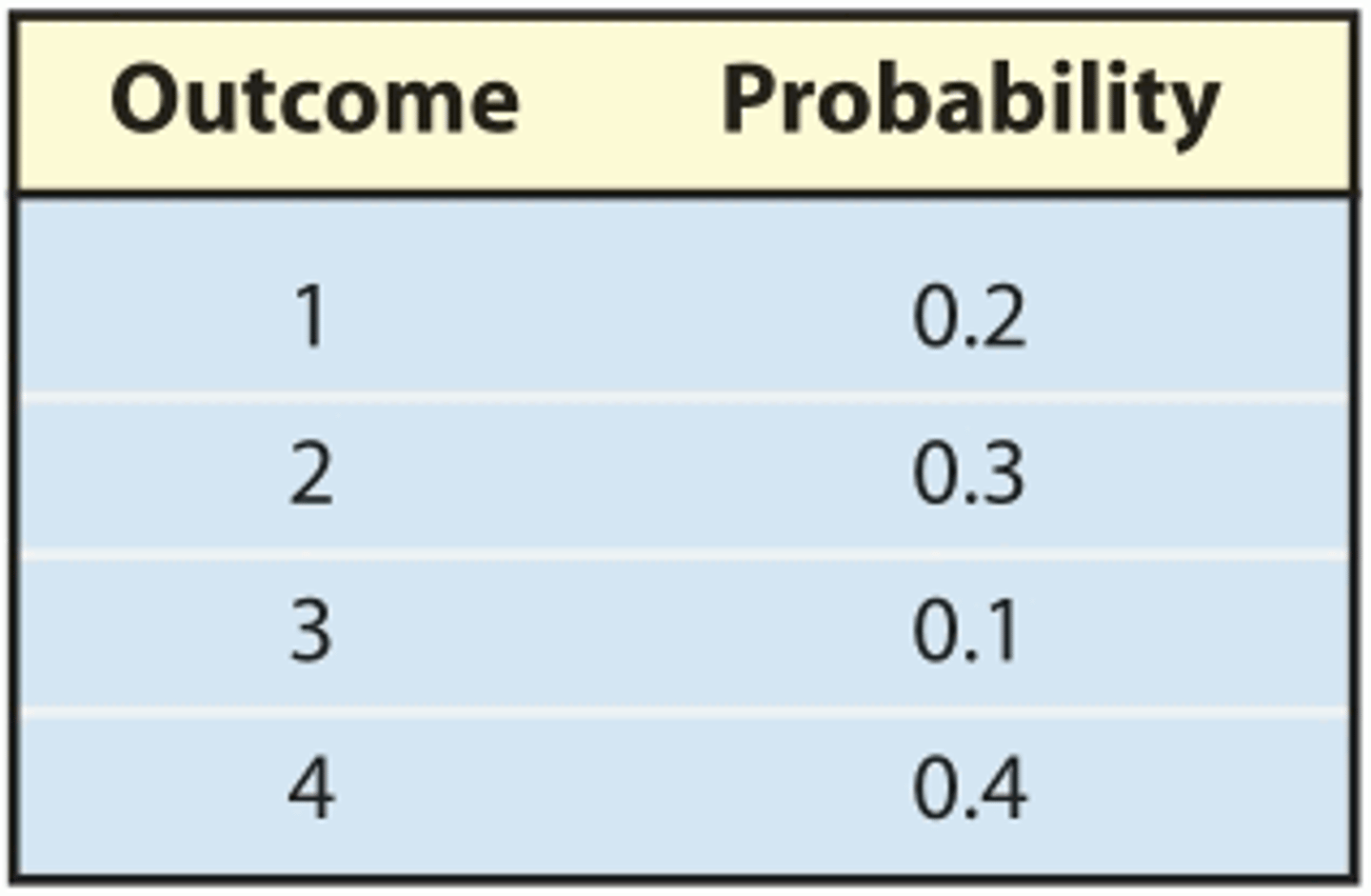
a probability is legitiment if

everything is between 0 and 1

all probability add up to 1

Wile E. Coyote is pursuing the Road Runner across Great Britain toward Scotland. The Road Runner chooses his route randomly, such that there is a probability of 0.8 that he'll take the high road and 0.2 that he'll take the low road. If he takes the high road, the probability that Wile E. Catches him is 0.01. If he takes the low road, the probability he gets caught is 0.05

The probability that he took the high road, given that he was caught

P(high road and caught) /

P(high road and caught)+P(low road and caught)

(0.8x0.01) /

(0.8x0.01 )+(0.2x0.05)

P=0.444